Estimation of Variable | set 1
Last Updated :
25 Jul, 2022
Variability: It is the import dimension that measures the data variation i.e. whether the data is spread out or tightly clustered. Also known as Dispersion When working on data sets in Machine Learning or Data Science, involves many steps – variance measurement, reduction, and distinguishing random variability from the real one. identifying sources of real variability, making decisions regarding the pre-processing choice or model selection based on it.
Terms related to Variability Metrics :
-> Deviation
-> Variance
-> Standard Deviation
-> Mean Absolute Deviation
-> Median Absolute Deviation
-> Order Statistics
-> Range
-> Percentile
-> Inter-quartile Range
- Deviation: We can call it – errors or residuals also. It is the measure of how different/dispersed the values are, from the central/observed value.
Example :
Sequence : [2, 3, 5, 6, 7, 9]
Suppose, Central/Observed Value = 7
Deviation = [-5, -4, -2, -1, 0, 2]
- Variance (s2): It is the best-known measure to estimate the variability as it is Squared Deviation. One can call it mean squared error as it is the average of standard deviation.

Example :
Sequence : [2, 3, 5, 6, 7, 9]
Mean = 5.33
Total Terms, n = 6
Squared Deviation = (2 - 5.33)2 + (3 - 5.33)2 + (5 - 5.33)2
(6 - 5.33)2 + (7 - 5.33)2 + (9 - 5.33)2
Variance = Squared Deviation / n
Code –
Python3
import numpy as np
Sequence = [2, 3, 5, 6, 7, 9]
var = np.var(Sequence)
print("Variance : ", var)
|
Output :
Variance : 5.5555555555555545
- Standard Deviation: It is the square root of Variance. Is also referred to as Euclidean Norm.
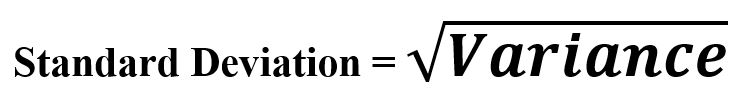
Example :
Sequence : [2, 3, 5, 6, 7, 9]
Mean = 5.33
Total Terms, n = 6
Squared Deviation = (2 - 5.33)2 + (3 - 5.33)2 + (5 - 5.33)2
(6 - 5.33)2 + (7 - 5.33)2 + (9 - 5.33)2
Variance = Squared Deviation / n
Standard Deviation = (Variance)1/2
Code –
Python3
import numpy as np
Sequence = [2, 3, 5, 6, 7, 9]
std = np.std(Sequence)
print("Standard Deviation : ", std)
|
Output :
Standard Deviation : 2.357022603955158
- Mean Absolute Deviation: One can estimate a typical estimation for these deviations. If we average the values, the negative deviations would offset the positive ones. Also, the sum of deviations from the mean is always zero. So, it is a simple approach to take the average deviation itself.

Example :
Sequence : [2, 4, 6, 8]
Mean = 5
Deviation around mean = [-3, -1, 1, 3]
Mean Absolute Deviation = (3 + 1 + 1 + 3)/ 4
Python3
import numpy as np
def mad(data):
return np.mean(np.absolute(
data - np.mean(data)))
Sequence = [2, 4, 6, 8]
print ("Mean Absolute Deviation : ", mad(Sequence))
|
Output :
Mean Absolute Deviation : 2.0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...