Error Detection Codes: Parity Bit Method
Last Updated :
12 May, 2023
Error Detection Codes : The binary information is transferred from one location to another location through some communication medium. The external noise can change bits from 1 to 0 or 0 to 1.This changes in values changes the meaning of actual message and is called error. For efficient data transfer, there should be an error detection and correction codes. An error detection code is a binary code that detects digital errors during transmission. To detect error in the received message, we add some extra bits to the actual data.
Without addition of redundant bits, it is not possible to detect errors in the received message. There are 3 ways in which we can detect errors in the received message :
1. Parity Bit
2. CheckSum
3. Cyclic Redundancy Check (CRC)
We’ll be understanding the parity bit method in this article in depth :-
Parity Bit Method : A parity bit is an extra bit included in binary message to make total number of 1’s either odd or even. Parity word denotes number of 1’s in a binary string. There are two parity system – even and odd parity checks.
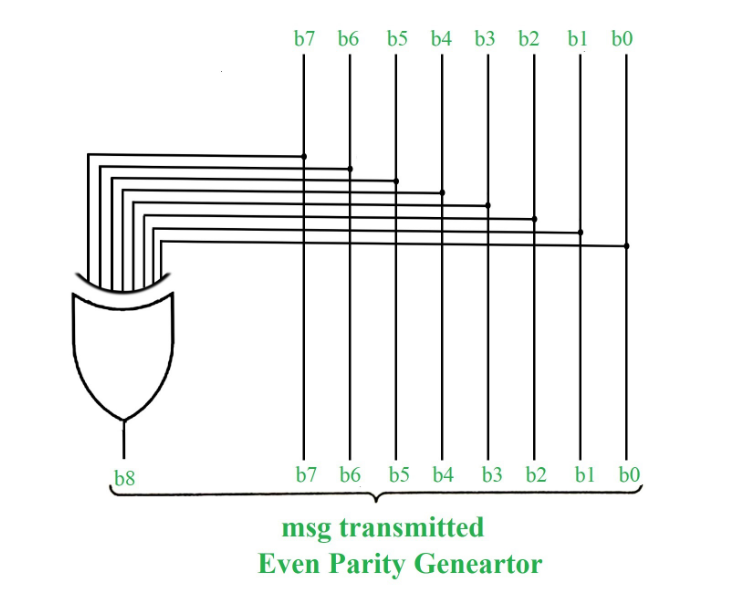
1. Even Parity Check: Total number of 1’s in the given data bit should be even. So if the total number of 1’s in the data bit is odd then a single 1 will be appended to make total number of 1’s even else 0 will be appended(if total number of 1’s are already even). Hence, if any error occurs, the parity check circuit will detect it at the receiver’s end. Let’s understand this with example, see the below diagram :

Even Parity Check (fig – 1.1)
In the above image, as we can see the data bits are ‘1011000’ and since this is even parity check that we’re talking about, 1 will be appended as the parity bit (highlighted in red) to make total count of 1’s even in the data sent. So here, our parity bit is 1. If the total count of 1 in the given data bits were already even, then 0 would’ve been appended.
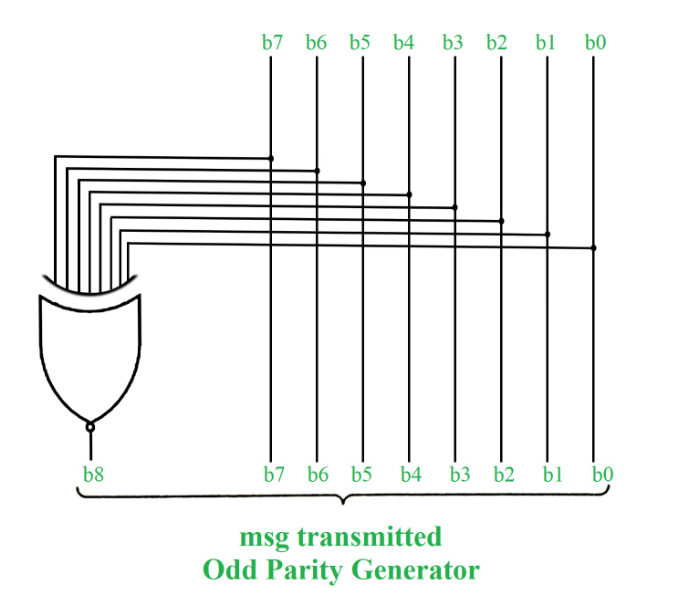
2. Odd Parity Check: In odd parity system, if the total number of 1’s in the given binary string (or data bits) are even then 1 is appended to make the total count of 1’s as odd else 0 is appended. The receiver knows that whether sender is an odd parity generator or even parity generator. Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or 0 to 1, received binary bit will have an even number of 1’s which will indicate an error.
Take reference from fig(1.1) and rather than appending the 1 as parity bit, append 0 because total number of 1’s are already odd.
Some more examples :-
| Message (XYZ) |
P(Odd) |
P(Even) |
| 000 |
1 |
0 |
| 001 |
0 |
1 |
| 010 |
0 |
1 |
| 011 |
1 |
0 |
| 100 |
0 |
1 |
| 101 |
1 |
0 |
| 110 |
1 |
0 |
| 111 |
0 |
1 |
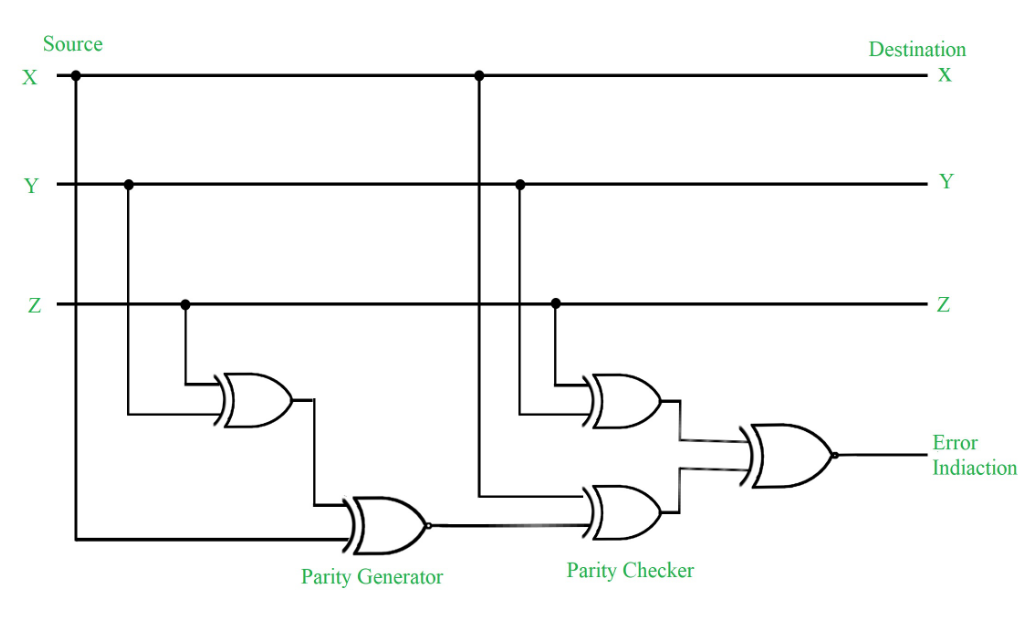 Figure – Error Detection with Odd Parity Bit
Figure – Error Detection with Odd Parity Bit
Limitations :
1. The limitation of this method is that only error in a single bit would be identified and we also cannot determine the exact location of error in the data bit.
2. If the number of bits in even parity check increase or decrease (data changed) but remained to be even then it won’t be able to detect error as the number of bits are still even and same goes for odd parity check.
See the below image for more details :

Can’t detect error (Even Parity Check)
In the above example, the the data bits has been changed but as we can see the total count of 1’s remain to be even, the error can’t be detected even though the message’s meaning has been changed. You can visualize the same for odd parity check the number of 1’s will remain odd, even if the data bits have been changed and the odd parity check won’t be able to detect error.
Points to Remember :
- In 1’s complement of signed number +0 and -0 has two different representation.
- The range of signed magnitude representation of an 8-bit number in which 1-bit is used as a signed bit as follows -27 to +27.
- Floating point number is said to be normalized if most significant digit of mantissa is one. For example, 6-bit binary number 001101 is normalized because of two leading 0’s.
- Booth algorithm that uses two n bit numbers for multiplication gives results in 2n bits.
- The booth algorithm uses 2’s complement representation of numbers and work for both positive and negative numbers.
- If k-bits are used to represent exponent then bits number = (2k-1) and range of exponent = – (2k-1 -1) to (2k-1).
Share your thoughts in the comments
Please Login to comment...