When an external force acts to do work, moving a body from a point to another against a force like spring force or gravitational force, that work gets collected or stores as the potential energy of the body. When the external force is excluded, the body moves, gaining the kinetic energy and losing an equal quantity of potential energy. The sum of kinetic and potential energies is hence conserved. Forces of this class are known as conservative forces. Examples of these forces are spring force and gravitational force.
Coulomb force is a conservative force between two (stationary) charges. Both have an inverse-square relationship on distance and differ only in the proportionality constants. The masses in the expression of gravitational law are replaced by charges in Coulomb’s law expression. Thus, like the potential energy of a mass in a gravitational field, the electrostatic potential energy of a charge in an electrostatic field is defined.
Equipotential Surface
A surface with a fixed potential value at all locations on the surface is known as an equipotential surface. For a single charge q, the potential can be expressed as
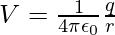
In the above expression, it is observed that if r is constant then V also remains constant. Therefore, equipotential surfaces of a single point charge are concentric spherical surfaces centered at the charge.
For a single charge q(a) equipotential surfaces are spherical surfaces centered at the charge, and(b) electric field lines are radial, starting from the charge if q > 0.
Depending on whether q is positive or negative, the electric field lines for a single charge q are radial lines that begin or finish at the charge. The electric field at each place is clearly normal to the equipotential surface that passes through that point. The equipotential surface through a point is normal to the electric field at that location for any charge arrangement. The proof for this assertion is straightforward.
The field has a non-zero component along the surface if it was not perpendicular to the equipotential surface. Work would be required to shift a unit test charge in the opposite direction as the component of the field. However, this contradicts the definition of an equipotential surface, which states that there is no potential difference between any two places on the surface and that no work is necessary to move a test charge over it. Therefore, at all points, the electric field must be normal to the equipotential surface. Equipotential surfaces allow an alternative visual image in addition to the image of electric field lines around a charge arrangement.
Equipotential surfaces for a uniform electric field.
For a uniform electric field E, say, along the x-axis, the equipotential surfaces are planes perpendicular to the x-axis, that is planes parallel to the y-z plane as shown in the above figure.
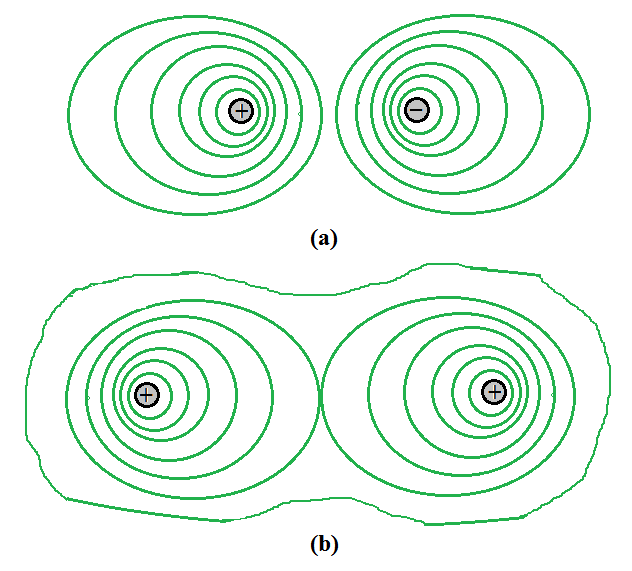
Some equipotential surfaces for (a) a dipole, (b) two identical positive charges.
The above figure is (a) Equipotential surfaces for a dipole and (b) Equipotential surfaces with two identical positive charges.
Work Done in Equipotential Surface
Moving a charge between two places on an equipotential surface is always zero. In an equipotential surface, if a point charge is transported from point A have potential energy VA to point B have potential energy VB, the work done to move the charge is given by
W = q(VA –VB) = 0
Because VA – VB = 0,
The total work done W is 0.
Properties of Equipotential Surface
- An equipotential surface has an electric field that is constantly perpendicular to it.
- It is impossible for two equipotential surfaces to intersect.
- Equipotential surfaces for a point charge are concentric spherical shells.
- For a uniform electric field, the equipotential surfaces are planes normal to the x-axis.
- The equipotential surface is directed from high potential to low potential.
- The potential inside a hollow charged spherical conductor is constant. Equipotential volume can be used to this. Moving a charge from the center to the surface requires no work done.
- The equipotential surface of an isolated point charge is a sphere. Different equipotential surfaces exist around the point charge, i.e. concentric spheres.
- Any plane normal to the uniform field direction is an equipotential surface.
- The distance between equipotential surfaces allows us to distinguish between strong and weak fields.
Electric Potential
The amount of work required to transport a unit charge from a reference point to a specific point against the electric field is known as electric potential.
When an object moves against an electric field, it gains energy that is referred to as electric potential energy. Divide the potential energy by the quantity of charge to get the charge’s electric potential. The electric field’s strength is determined by the electric potential. It is unrelated to whether or not a charge should be placed in the electric field. Electric potential is a scalar quantity. At point charge +q, all points with a distance of r have the same potential.
An object’s electric potential is determined by the following factors:
- An electric charge.
- The position of an electrically charged object in relation to other electrically charged objects.
Electric Potential Due to a Point Charge
Consider the origin of a point charge Q. Take Q to be positive. With position vector r from the origin, we want to find the potential at any point P. To do so, we must compute the amount of work required to transport a unit positive test charge from infinity to point P. When Q > 0, the work done on the test charge against the repulsive force is positive. We choose a handy path – along the radial direction from infinity to point P – since the work is done is independent of the path.
Work done in bringing a unit positive test charge from infinity to the point P, against the repulsive force of charge Q (Q > 0), is the potential at P due to the charge Q.
The electrostatic force on a unit positive charge at some intermediate point P′ on the path equals to
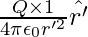
where ‘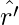
} is the unit vector along OP′ therefore, work done against this force from r′ to r′ + ∆r′ can be written as
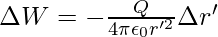
The negative sign represents ∆r′ < 0, ∆W is positive . Total work done (W) by the external force is determined by integrating the above equation both side, from r′ = ∞ to r′ = r,
![W=-\int_{∞}^{r} \frac{Q}{4\pi\epsilon_0r'^2}d{r'}\\ W=\left[\frac{Q}{4\pi\epsilon_0r'}\right]_∞^r\\ W=\frac{Q}{4\pi\epsilon_0r}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2e0180c3df582bd6cbe1919ff24155a_l3.png "Rendered by QuickLaTeX.com")
The potential at P due to the charge Q can be expressed as
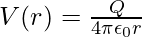
Sample Problems
Problem 1: Calculate the potential at a point P due to a charge of 4 × 10–7 C located 9 cm away.
Solution:
The potential at P due to the charge Q can be expressed as
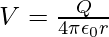
Substituting the cave in the above expression,
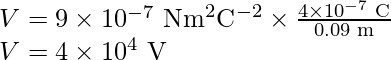
Problem 2: Obtain the work done in bringing a charge of 2 × 10–9 C from infinity to point P. Does the answer depend on the path along which the charge is brought? (V= 4 × 104 V)
Solution:
Given,
q= 2 × 10–9 C
V= 4 × 104 V
The expression for work don is
W = qV
Substitute the value in the above expression,
W = 2 × 10–9 C × 4 × 104 V
W = 8 × 10–5 J
No, the work done will be path independent. Any infinitesimal path can be broken down into two perpendicular displacements: one along to r and one perpendicular to r. The work done relation to the latter will be zero.
Problem 3: Determine the electrostatic potential energy of a system consisting of two charges 7 µC and –2 µC (and with no external field) placed at (–9 cm, 0, 0) and (9 cm, 0, 0) respectively.
Solution:
Given,
Two charges 7 µC and –2 µC.
Distance between two points is 0.18 m.
The expression for the electrostatic potential energy is,
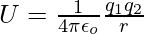
Substitute the value in the above expression,
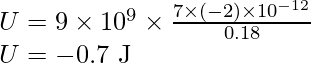
Problem 4: 6 A molecule of a substance has a permanent electric dipole moment of magnitude 10–29 C m. A mole of this substance is polarized (at low temperature) by applying a strong electrostatic field of magnitude 106 V m–1. The direction of the field is suddenly changed by an angle of 60º. Estimate the heat released by the substance in aligning its dipoles along the new direction of the field. For simplicity, assume 100% polarization of the sample.
Solution:
Here, dipole moment of each molecule = 10–29 Cm.
As 1 mole of the substance contains 6 × 1023 molecules.
Electrostatic field of magnitude 106 V m–1.
Total dipole moment of all the molecules can be written as
p = 6 × 1023 × 10–29 Cm
p = 6 × 10–6 Cm
Initial potential energy, Ui given by
Ui = –pE cos θ
Ui = –6×10–6×106 cos 0°
Ui = –6 J
Final potential energy (when θ = 60°), Uf
Uf = –6 × 10–6 × 106 cos 60°
Uf = –3 J
Change in potential energy = –3 J – (–6 J) = 3 J
So, there is loss in potential energy. This must be the energy released by the substance in the form of heat in aligning its dipoles.
Problem 5: Write the properties of Equipotential Surface.
Solution:
Following are the properties of equipotential surface.
- An equipotential surface has an electric field that is constantly perpendicular to it.
- It is impossible for two equipotential surfaces to intersect.
- Equipotential surfaces for a point charge are concentric spherical shells.
- For a uniform electric field, the equipotential surfaces are planes normal to the x-axis.
- The equipotential surface is directed from high potential to low potential.
- The potential inside a hollow charged spherical conductor is constant. Equipotential volume can be used to this. Moving a charge from the center to the surface requires no work done.
- The equipotential surface of an isolated point charge is a sphere. Different equipotential surfaces exist around the point charge, i.e. concentric spheres.
- Any plane normal to the uniform field direction is an equipotential surface.
- The distance between equipotential surfaces allows us to distinguish between strong and weak fields.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...