A famous British scientist Isaac Newton derived three equations of motion that describe the most fundamental concepts of motion of an object. These equations govern the motion of an object in one, two, and three dimensions. These equations are easily used to calculate the values or the expressions for the position, velocity, or acceleration of an object at various times. Let’s first understand the basic concept of motion and different terms related to it.
What is Motion?
Motion can be described as a change in the position of the object with respect to time. Position can be measured using a reference point and calculating the distance of the object from the reference point. Time can be calculated using a speed watch which will determine the time taken to change the position. There are many great scientists who worked and derived some equation or theory to study motion like Galileo Galilei and Isaac Newton.

The motion of a car in a time interval
Before discussing the equation of motion, let’s first revise the basic terms related to the motion of an object. The motion of an object can be described using four different terms that are as follows:
Distance
The actual measure of the total change in the position of an object (in a particular time period) is called the Distance.
Distance (d) is a scalar quantity and hence, gives the magnitude only.
e.g. Consider the figure below, there is a car moving from position A to position B. The speedometer in the car will show the distance traveled from point A to point B.

Distance traveled by car
Displacement
The shortest measure of the net change in the position of an object (in a specific time interval) is called displacement.
Displacement is a vector quantity and hence, gives both a magnitude and the direction.
e.g. Consider the figure below, there is a car moving from position A to position B. The displacement is equal to the distance covered in a certain direction of the motion.

Displacement of the car
Read More, Distance and Displacement
Speed
The speed of an object is the measure to determine how fast or slow the object move or changes its position.
Speed is equal to the time rate change in the distance covered by the object.
e.g. Suppose a fan which is running very fast, but it is fast with respect to your stationary state, if you will also spin at the same speed as the fan you will see it is not even moving.
Mathematically, the speed of an object is given as:
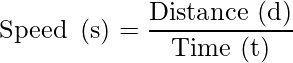
Since, both time and distance are scalar quantities therefore, speed is also a scalar quantity.
The SI unit of speed is m/s.
Velocity
The rate of change of displacement of an object with respect to time, or the rate of change of position, is called velocity.
Graphically, it is the slope of the displacement function. It is a vector quantity and thus gives both a magnitude and direction.
Mathematically, the velocity is defined as:
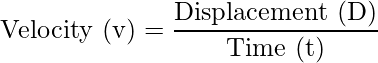
The SI unit of velocity is same as the speed that is, m/s. The difference between the speed and velocity of an object is that, the speed is a scalar quantity while the velocity is a vector quantity.
Acceleration
The change in velocity of an object per unit time, or the rate of change of velocity function with respect to time, is defined as the acceleration.
Graphically, it is the slope of the velocity function. Acceleration is a vector quantity and thus gives both a magnitude and direction.
Mathematically, the acceleration is defined as:
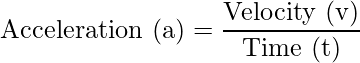
What are the equations of motion?
The equations that explain the nature and the behavior of a physical system in terms of its motion as a function of time are called the equations of motion. There are three equations of motion that can be used to calculate the components of motion like distance, displacement, velocity (initial and final), time (t), and acceleration (a) of an object. The following are the three equation of motion:
- First Equation of Motion: v = u + at
- Second Equation of Motion: s = ut + 1/2(at2)
- Third Equation of Motion: v2 = u2 – 2as
where, v and u are the initial and the final velocities, a is the acceleration, t is the time taken and s is the displacement of an object.
Derivation of Equations of Motion
On the basis of the purpose of the application of different components in different solutions, there are three different ways to derive these equations:
- Derivation of the equations of motion algebraically, using the definition and different formulae of the components of the motion.
- Derivation of the equations of motion graphically, using the graphical representation for distance, velocity and acceleration of an object.
- Derivation of the equations of motion using integral method.
Here, in the present article, the derivation of the three equations of motion are discussed graphically as:
Derivation of First equation of motion graphically:
The first equation relates velocities with the acceleration and time of the object. Therefore, this equation is applicable when displacement is not given and so is also known as velocity-time relation.
Consider a velocity-time graph as shown below, the velocity of the body changes from A to C in time t at a uniform rate. The distance from A to the x-axis is the final velocity and OC is the total time t.
A perpendicular is drawn from B to OC, a parallel line is drawn from A to D, and another perpendicular is drawn from B to OE (represented by dotted lines).
The plot shows that the object has a variable velocity that is increasing from u to v as the slope is positive velocity is increasing in a positive direction.

The velocity-time graph
Now we will calculate the acceleration using this motion graph. Acceleration is the tangent of the angle in v-t graph.
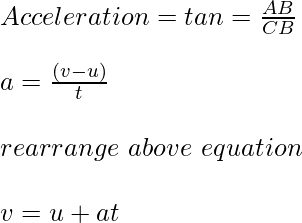
Derivation of Second equation of motion graphically:
Below v-t graph shows the velocity and time relationship of an object with an initial velocity of u m/s and final velocity of v m/s. As we know the area of the v-t graph gives the displacement of the object, so we will calculate the area of the graph and find out the equation of displacement. The same graph we have used in the previous derivation but here the approach will be different, earlier we used the slope to calculate acceleration, but now we will use area.

v-t Motion Graph
The Displacement of the object (d) = Area of triangle ABC + Area of rectangle BCOT
Here, the area of the triangle ABC = 1/2 × Base × Height
= 1/2 × t × (v-u)
And the area of the rectangle BCOT = Length × Width
= u × t
Therefore, the displacement of the object, d = 1/2 × t × (v-u) + u × t ……(1)
Also, from the first equation of motion, v – u = at
Substitute at for v-u in the equation (1),
d = 1/2 × t × (at) + u × t
d = ut + (1/2)at2
Derivation of Third equation of motion graphically:
We have different ways to calculate areas, like dividing any form into small pieces and then adding up the area of converting the problem to a shape that is well known to us. In this derivation, the area of a rectangular shape is converted and the displacement is calculated using the area of a rectangle. This equation is used when time is not given.

Original graph to highlighted graph
Here, P is the Centre point, so the speed of the object is (v + u) / 2.
Therefore, the displacement of the object (d) = the area of the triangle ABC + the area of the rectangle ACTO = the area of the rectangle OPQT
The displacement of the object, d = Length × Width
= t × (v + u) / 2 ……(2)
Also, from the first equation of motion, v – u = at or t = (v – u) / a
Therefore, the equation (2) becomes:
d = (v – u) / a × (v + u) / 2
v2 = u2 – 2ad
Read More,
Sample Problems
Problem 1: Speed-time graph for a particle is given below, find the distance covered by the particle in 40 minutes.

Speed-Time Plot
Solution:
Calculating distance using the area under the speed-time graph.

Area under the given curve.
Distance covered by the particle in 40 min = Area under the given curve.
The shape formed under the curve is of a rectangle therefore, the area under the curve = length × width.
Here, the length of the shape is equivalent to the time taken i.e. 40 min or 40 min × 60 s/1 min = 2400 s.
Similarly, the width of the shape is equivalent to the speed i.e. 15 km/h or 15 km/h × 1 h/3600 s × 1000 m/1 km = 4.17 m/s.
Therefore, the area under the curve or the distance covered in 40 min is given by:
⇒ 2400 s × 4.17 m/s = 10000 m or 10 km.
Hence, the distance covered by the particle in 40 min is equal to 10 km.
Problem 2: For the Below, graph calculates the distance covered by the particle between the time 20 minutes to 40 minutes.

Speed-Time plot
Solution:
Distance covered by the particle from time t = 20 min to 40 min is equal to the Area under the given curve between the given time range.

Highlighted Area of Speed-time Plot
The shape formed under the curve is of a rectangle therefore, the area under the curve = length × width.
Here, the length of the shape is equivalent to the time taken i.e. (40 – 20) min or 20 min × 60 s/1 min = 1200 s.
Similarly, the width of the shape is equivalent to the speed i.e. 15 km/h or 15 km/h × 1 h/3600 s × 1000 m/1 km = 4.17 m/s.
Therefore, the area under the curve or the distance covered from time t = 20 min to 40 min is given by:
⇒ 1200 s × 4.17 m/s = 5004 m or 5.004 km.
Hence, the distance covered by the particle from time t = 20 min to 40 min is equal to 5.004 km.
Problem 3: Find the distance covered by a particle during the time interval t = 0 s and t = 4 s for which the speed-time graph is given below:

Speed-time plot
Solution:

Speed-Time Graph
Distance covered by the particle in t = 0 s and t = 4 s is equal to area under the curve.
The shape formed under the curve is of a triangle therefore, the area under the curve = 1/2 × base × height.
Here, the base of the shape is equivalent to the time taken i.e. 4 s.
Similarly, the height of the shape is equivalent to the speed i.e. 20 m/s.
Therefore, the area under the curve or the distance covered in t = 0 s and t = 4 s is given by:
⇒ 1/2 × 4 s × 20 m/s = 40 m.
Hence, the distance covered by the particle in t = 0 s and t = 4 s is equal 40 m.
Problem 4: The figure below shows the distance-time graph of three objects A, B, and C. Determine:
(a) which object is moving with a greater speed?
(b) which object is moving with a lesser speed?

Distance-Time Plot
Solution:
The given graph is distance time graph and the slope gives us the value of speed i.e. more the slope more is speed.
As it is observed from the given graph, A has maximum slope, so it is moving with greater speed and C has the least slope, so it is moving with the slowest speed.
Problem 5: Calculate the speed of the particle with the help of the given distance-time motion graph.

Distance-Time Plot
Solution:
Here, the speed of the particle is equal to the slope of the graph.
And the slope of the distance graph is equal to the speed of the particle.
Therefore, the formula to calculate the speed of the particle is:
Speed = Distance / Time
= 20 m / 5 s
= 4 m/s.
Hence, the speed of the particle is equal to 4 m/s.
Share your thoughts in the comments
Please Login to comment...