Equation of circle from center and radius
Last Updated :
23 Jul, 2022
Given the center of circle (x1, y1) and its radius r, find the equation of the circle having center (x1, y1) and having radius r.
Examples:
Input : x1 = 2, y1 = -3, r = 8
Output : x^2 + y^2 – 4*x + 6*y = 51.
Input : x1 = 0, y1 = 0, r = 2
Output : x^2 + y^2 – 0*x + 0*y = 4.
Approach:
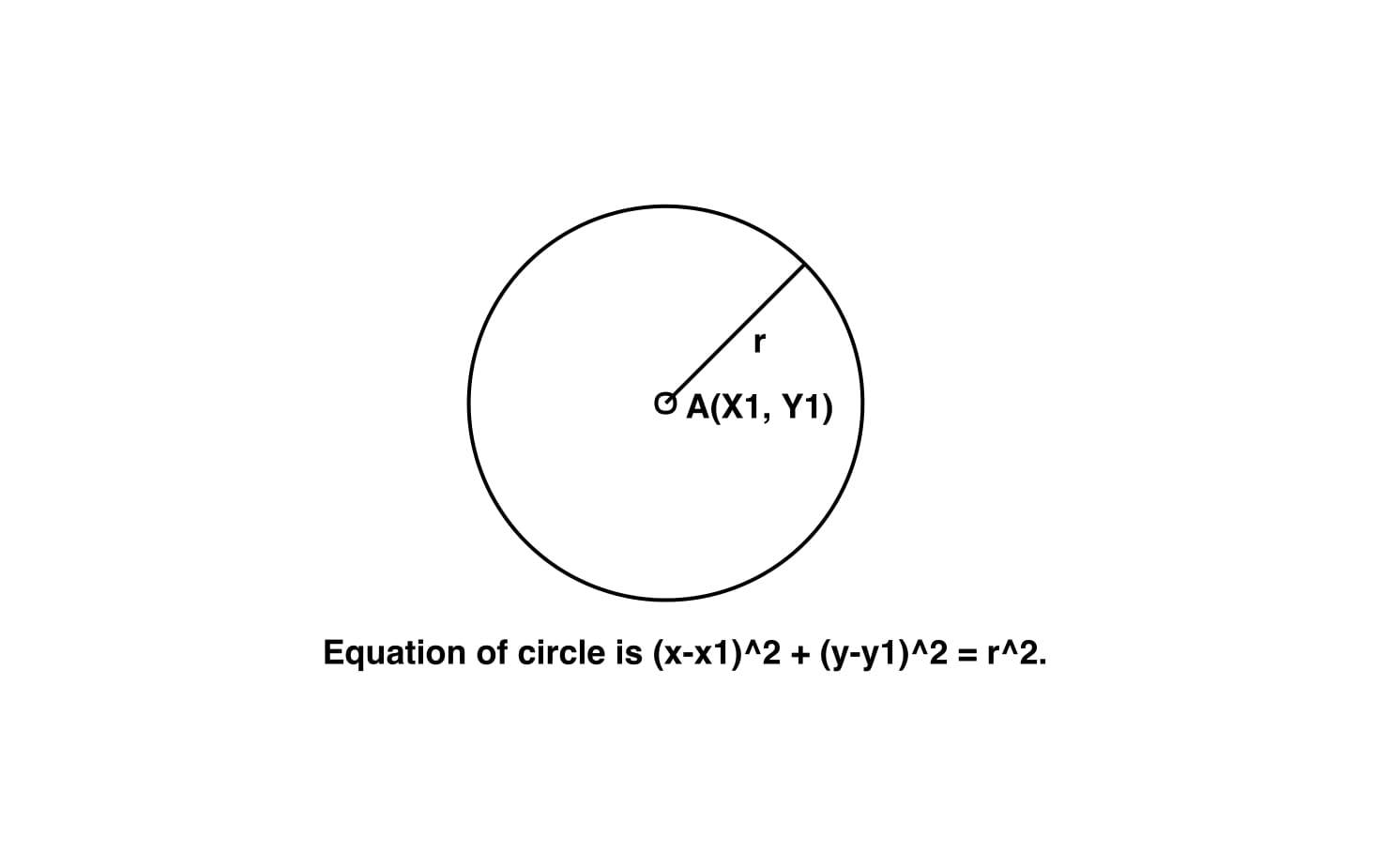
Given the center of circle (x1, y1) and its radius r, we have to find the equation of the circle having center (x1, y1) and having radius r.
the equation of circle having center (x1, y1) and having radius r is given by :-
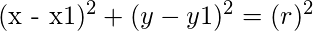
on expanding above equation
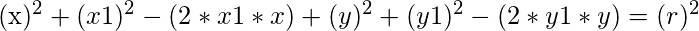
on arranging above we get
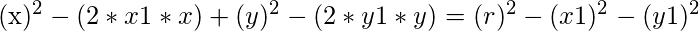
Below is the implementation of above approach:
C++
#include <iostream>
using namespace std;
void circle_equation(double x1, double y1, double r)
{
double a = -2 * x1;
double b = -2 * y1;
double c = (r * r) - (x1 * x1) - (y1 * y1);
cout << "x^2 + (" << a << " x) + ";
cout << "y^2 + (" << b << " y) = ";
cout << c << "." << endl;
}
int main()
{
double x1 = 2, y1 = -3, r = 8;
circle_equation(x1, y1, r);
return 0;
}
|
Java
import java.util.*;
class solution
{
static void circle_equation(double x1, double y1, double r)
{
double a = -2 * x1;
double b = -2 * y1;
double c = (r * r) - (x1 * x1) - (y1 * y1);
System.out.print("x^2 + (" +a+ " x) + ");
System.out.print("y^2 + ("+b + " y) = ");
System.out.println(c +"." );
}
public static void main(String arr[])
{
double x1 = 2, y1 = -3, r = 8;
circle_equation(x1, y1, r);
}
}
|
Python3
def circle_equation(x1, y1, r):
a = -2 * x1;
b = -2 * y1;
c = (r * r) - (x1 * x1) - (y1 * y1);
print("x^2 + (", a, "x) + ", end = "");
print("y^2 + (", b, "y) = ", end = "");
print(c, ".");
x1 = 2;
y1 = -3;
r = 8;
circle_equation(x1, y1, r);
|
C#
using System;
class GFG
{
public static void circle_equation(double x1,
double y1,
double r)
{
double a = -2 * x1;
double b = -2 * y1;
double c = (r * r) - (x1 * x1) - (y1 * y1);
Console.Write("x^2 + (" + a + " x) + ");
Console.Write("y^2 + ("+ b + " y) = ");
Console.WriteLine(c + "." );
}
public static void Main(string []arr)
{
double x1 = 2, y1 = -3, r = 8;
circle_equation(x1, y1, r);
}
}
|
PHP
<?php
function circle_equation($x1, $y1, $r)
{
$a = -2 * $x1;
$b = -2 * $y1;
$c = ($r * $r) - ($x1 * $x1) -
($y1 * $y1);
echo "x^2 + (" . $a . " x) + ";
echo "y^2 + (" . $b . " y) = ";
echo $c . "." . "\n";
}
$x1 = 2; $y1 = -3; $r = 8;
circle_equation($x1, $y1, $r);
?>
|
Javascript
<script>
function circle_equation(x1, y1, r)
{
let a = -2 * x1;
let b = -2 * y1;
let c = (r * r) - (x1 * x1) -
(y1 * y1);
document.write( "x^2 + (" +a + " x) + ");
document.write( "y^2 + (" +b+ " y) = ");
document.write( c+ "<br>");
}
let x1 = 2;
let y1 = -3;
let r = 8;
circle_equation(x1, y1, r);
</script>
|
Output: x^2 + (-4 x) + y^2 + (6 y) = 51.
Time complexity: O(1), since there is no loop or recursion.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...