Equation of a straight line with perpendicular distance D from origin and an angle A between the perpendicular from origin and x-axis

Given two integers D and A representing the perpendicular distance from the origin to a straight line and the angle made by the perpendicular with the positive x-axis respectively, the task is to find the equation of the straight line.

Examples:

Input: D = 10, A = 30 degrees
Output: 0.87x +0.50y = 10

Input: D = 12, A = 45 degrees
Output: 0.71x +0.71y = 12

Approach: The given problem can be solved based on the following observations:

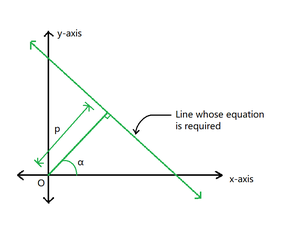
Figure 1

• Let the perpendicular distance be (p) and the angle between the perpendicular and the positive x-axis be (α) degrees.
• Consider a point P with coordinates (x, y) on the required line.
• Draw a perpendicular from P to meet the x-axis at L.
• From L, draw a perpendicular on OQ at M.
• Now, draw a perpendicular from P to meet ML at N.

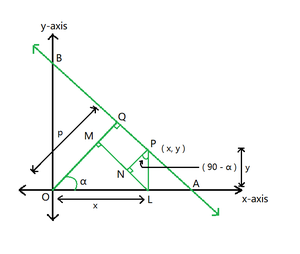
Figure 2

Now consider right triangle OLM

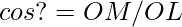
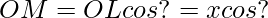 — (1)

Now consider right triangle PNL



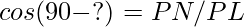
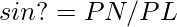
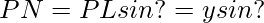
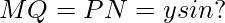 — (2)

Now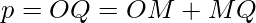 
Using equations (1) and (2)
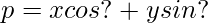 which is the equation of the required line

Below is the implementation of the above approach :

C++

// C++ program for the approach
#include <bits/stdc++.h>
using namespace std;

// Function to find equation of a line whose
// distance from origin and angle made by the
// perpendicular from origin with x-axis is given
void findLine(int distance, float degree)
{
    // Convert angle from degree to radian
    float x = degree * 3.14159 / 180;

    // Handle the special case
    if (degree > 90) {
        cout << "Not Possible";
        return;
    }

    // Calculate the sin and cos of angle
    float result_1 = sin(x);
    float result_2 = cos(x);

    // Print the equation of the line
    cout << fixed << setprecision(2)
         << result_2 << "x +"
         << result_1 << "y = " << distance;
}

// Driver Code
int main()
{
    // Given Input
    int D = 10;
    float A = 30;

    // Function Call
    findLine(D, A);

    return 0;
}

Java

// Java program for the approach

class GFG{

// Function to find equation of a line whose
// distance from origin and angle made by the
// perpendicular from origin with x-axis is given
static void findLine(int distance, float degree)
{
    // Convert angle from degree to radian
    float x = (float) (degree * 3.14159 / 180);

    // Handle the special case
    if (degree > 90) {
        System.out.print("Not Possible");
        return;
    }

    // Calculate the sin and cos of angle
    float result_1 = (float) Math.sin(x);
    float result_2 = (float) Math.cos(x);

    // Print the equation of the line
    System.out.print(String.format("%.2f",result_2)+ "x +"
         + String.format("%.2f",result_1)+ "y = " +  distance);
}

// Driver Code
public static void main(String[] args)
{
    // Given Input
    int D = 10;
    float A = 30;

    // Function Call
    findLine(D, A);

}
}

// This code is contributed by shikhasingrajput

Python3

# Python3 program for the approach
import math

# Function to find equation of a line whose
# distance from origin and angle made by the
# perpendicular from origin with x-axis is given
def findLine(distance, degree):

    # Convert angle from degree to radian
    x = degree * 3.14159 / 180

    # Handle the special case
    if (degree > 90):
        print("Not Possible")
        return

    # Calculate the sin and cos of angle
    result_1 = math.sin(x)
    result_2 = math.cos(x)

    # Print the equation of the line
    print('%.2f' % result_2,
          "x +", '%.2f' % result_1,
          "y = ", distance, sep = "")

# Driver code

# Given Input
D = 10
A = 30

# Function Call
findLine(D, A)

# This code is contributed by mukesh07

C#

// C# program for the approach
using System;
class GFG
{

    // Function to find equation of a line whose
    // distance from origin and angle made by the
    // perpendicular from origin with x-axis is given
    static void findLine(int distance, float degree)
    {
        // Convert angle from degree to radian
        float x = (float)(degree * 3.14159 / 180);

        // Handle the special case
        if (degree > 90) {
            Console.WriteLine("Not Possible");
            return;
        }

        // Calculate the sin and cos of angle
        float result_1 = (float)(Math.Sin(x));
        float result_2 = (float)(Math.Cos(x));

        // Print the equation of the line
        Console.WriteLine(result_2.ToString("0.00") + "x +"
             + result_1.ToString("0.00") + "y = " + distance);
    }

  static void Main ()
  {
    // Given Input
    int D = 10;
    float A = 30;

    // Function Call
    findLine(D, A);
  }
}

// This code is contributed by suresh07.

Javascript

<script>

        // JavaScript program for the above approach

        // Function to find equation of a line whose
        // distance from origin and angle made by the
        // perpendicular from origin with x-axis is given
        function findLine(distance, degree) {
            // Convert angle from degree to radian
            let x = degree * 3.14159 / 180;

            // Handle the special case
            if (degree > 90) {
                document.write("Not Possible");
                return;
            }

            // Calculate the sin and cos of angle
            let result_1 = Math.sin(x);
            let result_2 = Math.cos(x);

            // Print the equation of the line
            document.write(result_2.toPrecision(2) + "x + "
             + result_1.toPrecision(2) + "y = " + distance);
        }

        // Driver Code

        // Given Input
        let D = 10;
        let A = 30;

        // Function Call
        findLine(D, A);

        // This code is contributed by Hritik

</script>

Output:

0.87x +0.50y = 10

Time Complexity: O(1)
Auxiliary Space: O(1)