Episodic Memory and Deep Q-Networks

Episodic Memory:

Episodic Memory is a category of long-term memory that involves recent recollection of specific events, situations, and experiences. For Example Your first day at college. There are two important aspects of episodic memory are Pattern Separation and Pattern Completion.

Semantic Memory is used in many ways in machine learning such as Transfer Learning, Sequences like LSTM, catastrophic forgetting, etc. but if you design intelligent agents, we can use aspects of episodic memory for our purposes.

Episodic Memory in machine Learning: 

The value of episodic memory in Deep Reinforcement Learning is increasing, as many new Reinforcement learning papers using Episodic Memory in their agent architecture. In a DRL-based agent, this often takes the form of adding an external memory similar to the form of adding an external memory system, similar to the form of differential neural computers to the agent’s policy networks that decide which action to take or not.

A step towards answering these questions might be examining the mammalian episodic memory. The hippocampal formation is thought by many to be involved in memory in general and episodic memory in particular.

Organization of Episodic Memory: 

We have stated that the episodic memory system tracks the changes in the agent’s belief, but we have not articulated how such memory is organized and how information is stored and retrieved.

For a memory system to be effective, we must satisfy three properties:

• Storage of accurate memory from a single exposure to the environment.
• To retrieve the memory from a partial cue.
• Ability to store and recall a large amount of experience.

Architecture: 

There are many architectures that are proposed for using Episodic Memory in Reinforcement Learning, We are discussing here the “Episodic Memory Deep Q-Networks” paper which is proposed by researchers at Microsoft Research.

• Deep Q-Networks (DQN): A well-established technique to perform the above task is Q-learning, where we decide on a function called Q-function which is important for the success of the algorithm. DQN uses the neural networks as Q-function to approximate the action values Q(s, a, \theta) where 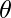 the parameter of network and (s,a) represents the state-action pair. Two important components of DQN are target network and experience relay. The parameter of neural networks are optimized using stochastic gradient descent to minimize the loss function:

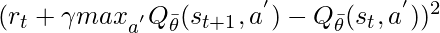
where r_t represents reward at t, \gamma is a discount factor and \bar{\theta} is the parameter of the target network.

• Episodic Memory Deep Q-Networks (EMDQN): Generally episodic memory is used for direct control by introducing a near deterministic environment to improve data efficiency in RL. In this paper, the authors use Episodic Control to accelerate the training of DQN. The agent is able to rapidly latch on high rewarding policies, even though it maintains the NN training that performs slow optimization for state generalization. This algorithm leverages the strength of both systems, one simulates the striatum that provides the inference target, which is denoted by S, another simulates the hippocampus that provides memory target that is generated by H. Therefore, our new loss function is :
•  .
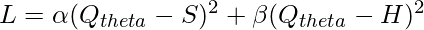• where Q_θ is known as the value function parameterized by θ.
• 
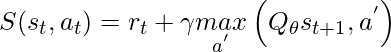
• The memory target H is defined as the best memorized return as follows:
• 
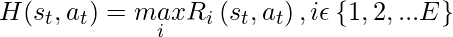
• where, E represents number of episodes the agent has faced and R_i(s, a) represents future return when taking action a under state s in i-th episode. The advantage of using this model is:
  • Faster Rewards Propagation: EMDQN uses the maximum return from episodic memory to propagate rewards, making up for the disadvantage of slow-learning resulted by single step reward update. For near-deterministic environments, each reward contained in episodic memory is by far the optimal. Therefore, using memory target H, the rewards in the best trajectories can be propagated to parameters of Q_θ(s, a).
  • Combination of Two Learning Models: By combining Episodic Memory and Deep Q-Network, the network will better simulate human brain, the objective function is like:

Where, D is the mini-batch of episodes. Adding parameter like 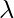 provides additional flexibility of switching between episodic memory and Deep Q-Network.

• High sample efficiency: EMDQN introduces a method to capture more information of samples. During training, it filters the best return from episodic memory and incorporates the knowledge into the neural network, which makes use of the samples more efficiently. In the previous RL algorithms, all samples, regardless of the rewards, are sampled uniformly, which leads to poor training performance because of the frequent appearance of zero rewards.

Below is the architecture of this EMDQN method:

EMDQN architecture

The state s represented by 4 history frames is processed by convolution neural networks, and forward-propagated by two fully connected layers to compute Q_θ(s, a). State s is multiplied by a random matrix drawn from Gaussian distribution and projected into a vector h, and passed into memory table to look up corresponding value H(s, a), and then H(s, a) is used to regularize Q_θ(s, a). For efficient lookup into the table, we use kd-Tree to construct the memory table. All experience tuples along with each episodic trace are cached. . Similar to the target network in DQN, it maintains a target memory table to provide stable memory value which is updated using previously cached transition.

Implementation

• In this implementation, we will be training EMDQN on the Pong game. For this purpose, we will be using Collaboratory.

Python3

# clone the original EMDQN repository
! git clone https://github.com/LinZichuan/emdqn

# switch to TensorFlow v1.0 to run this.
%tensorflow_version 1.x

# Install required modules
! cd emdqn && pip install -e .

# run train.py file in atari folder
# Due to resource constraint we will take (2 * 10^6) steps.
# The original paper runs on 4e7 epoch.
! cd emdqn/baselines/deepq/experiments/atari && python train.py --emdqn --steps 2e6

# Plot Reward with steps
import matplotlib.pyplot as plt
import pandas as pd
df =pd.read_csv('/content/emdqn/baselines/deepq/experiments/atari/result_Pong_True',
                header=None)
plt.plot(df[0],df[1])

qec_mean: -1.5634830438441465
qec_fount: 0.93
------------------------------------
| % completion          | 1        |
| steps                 | 1.97e+06 |
| iters                 | 4.91e+05 |
| episodes              | 470      |
| reward (100 epi mean) | -19.1    |
| exploration           | 0.01     |
------------------------------------

ETA: 1 minute

------------------------------------
| % completion          | 1        |
| steps                 | 1.98e+06 |
| iters                 | 4.93e+05 |
| episodes              | 471      |
| reward (100 epi mean) | -19      |
| exploration           | 0.01     |
------------------------------------

ETA: less than a minute

------------------------------------
| % completion          | 1        |
| steps                 | 1.99e+06 |
| iters                 | 4.95e+05 |
| episodes              | 472      |
| reward (100 epi mean) | -18.9    |
| exploration           | 0.01     |
------------------------------------

ETA: less than a minute

Steps vs Rewards

• From the above graph, it can be concluded that as the number of steps increasing, the model is performing better on the Pong game task with a greater improvement in reward after 1.5 million rewards. The original model is trained on 47 million epoch, due to time & resource constraints and limited memory of colab, we can’t train that much.

References:

• Episodic Memory and Deep Q- Network