Energy stored in a Capacitor
Last Updated :
12 Feb, 2022
Capacitors are used in almost every electronic device around us. From a fan to a chip, there are lots of capacitors of different sizes around us. Theoretically, the basic function of the capacitor is to store energy. Its common usage includes energy storage, voltage spike protection, and signal filtering. It was invented by a German scientist, Ewald Georg von Kleist, in 1745. Physically, a capacitor is just two conductors which are separated by an insulator. They are able to hold a charge which gives rise to a lot of their properties. Let’s study these properties in detail.
Capacitors and Capacitance
A capacitor is a system of two charges that are separated by an insulator. Let’s say the two conductors have a charge of Q1 and Q2 and potential V1 and V2. Usually, the charges are Q and -Q. The electric field in this region is proportional to the charge on the surface of capacitors. The figure below shows two conductors with charges Q and -Q on them. These conductors are separated by an insulator.

Now it is known that potential is nothing but the work done to bring the charge from the infinite to the present position. In this way, the potential also becomes proportional to the charge on the conductors. This means that the ratio of charge and potential is constant. The ratio is termed capacitance.
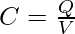
Although any shape and size works for making a capacitor, in real life most of these capacitors are cylindrical. While doing calculations and for the symbol, the capacitor is denoted as a parallel plate capacitor.
Parallel Plate Capacitor
A parallel plate capacitor consists of two large parallel planes separated by a small distance. Most of the time, the medium between the plates is considered to be a vacuum, but it can be any insulator material. The figure shows the diagram of a parallel plate capacitor that is connected to a battery.

Energy stored in a Capacitor
When a battery is connected across the plates of a capacitor, the current charges the capacitor, leading to the accumulation of the charges on the opposite plates. As the charges accumulate, the potential difference between the plates starts increasing. Let’s say the capacitance of the capacitor is “C”, it was uncharged initially. Now, after being connected to the battery, let’s say there is a potential difference, “V” that develops between the plates. Consider “q” as the charge on the plates at that time. Then,
q = CV
Work done to bring the charge from infinity to the potential of “V” is given by,
W = qV
Suppose the battery delivers a charge of “dq” to the plates while keeping the potential constant. Then,
W = dq.V = 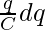
In this way, a total charge “q” is transferred from the battery to the capacitor. Then, the work done will be given by
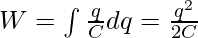
So, the energy stored in the capacitor is,
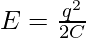
Using the previous relationship, q = CV
Energy can be re-written as,
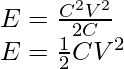
Using relationship, C= q/V
Energy can be written as,
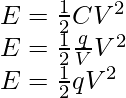
Therefore, the three formulae obtained for Energy stored in a capacitor,
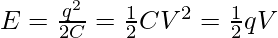
Sample Problems
Question 1: Find the capacitance if a charge of 3C and potential of 9V is maintained on plates.
Solution:
The relation for capacitance is given by,
q = CV
Given: q = 3C and V = 9V
q = CV
⇒ 3 = C(9)
⇒ 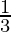 = C
= C
C = 0.333F
Question 2: Find the capacitance if a charge of 18C and the potential of 3V is maintained between the plates.
Solution:
The relation for capacitance is given by,
q = CV
Given: q = 18C and V = 3V
q = CV
⇒ 18 = C(3)
⇒ 6 = C
C = 6F
Question 3: Find the capacitance if a charge of 1C and the potential of 2V is maintained between plates.
Solution:
The relation for capacitance is given by,
q = CV
Given: q = 1C and V = 2V
q = CV
⇒ 1 = C(2)
⇒ 0.5 = C
C = 0.5F
Question 4: Find the energy stored in the capacitor of 12pF which is connected to a battery of 10V.
Solution:
The relation for energy stored in a capacitor is given by,
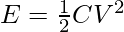
Given: C = 12pF and V = 10V
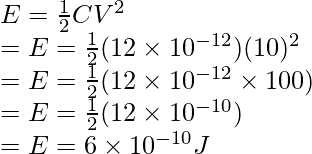
Question 5: Find the energy stored in the capacitor which has a charge of 9 x 10-5C and is connected to a battery of 10V.
Solution:
The relation for energy stored in a capacitor is given by,
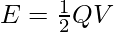
Given: q = 9 x 10-5 and V = 10V
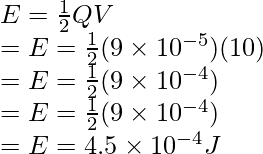
Question 6: Find the energy stored in the capacitor of 3pF which has a charge of 9 x 10-5C.
Solution:
The relation for energy stored in a capacitor is given by,
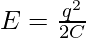
Given: q = 9 x 10-5 and C = 3 x 10-12
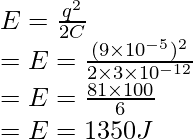
Question 7: A capacitor of capacitance “C”, is first connected to a battery of voltage V and fully charged, then it is connected to a battery of voltage 2V. Find the electrostatic energy gained/lost in this process.
Solution:
First, the capacitor is connected to a battery of the potential V.
Energy of the capacitor after full charge,
E1 = 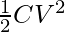
After it is connected to another battery,
E2 = 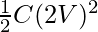
⇒E2 = 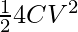
Energy change in this process = E2 – E1
= 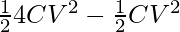
= 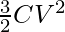
Since, the energy change is positive. Electrostatic energy was gained in the process.
Share your thoughts in the comments
Please Login to comment...