Open In App

Electric Potential Due to a Point Charge

Last Updated : 14 Jul, 2021
Improve
Improve
Like Article
Like
Save
Share
Report

Electric forces are responsible for almost every chemical reaction within the human body. These chemical reactions occur when the atoms and their charges collide together. In this process, some molecules are formed and some change their shape. Electric forces are experienced by charged bodies when they come under the influence of an electric field. These forces depend on the direction of the electric field and the charge placed in that field. When charges are moved around in the electric field, these forces do work on the charge and that gets stored in the form of electrostatic potential energy. Let’s look at concepts of electrostatic potential and electrostatic potential energy in detail. 

Electric Potential Energy

Electric potential energy is the energy that is required to move a charge against an electric field. When a charge is kept in an electric field, it experiences a force. So, to move against the force, we need to do work and that work gets stored in the charge in the form of electric potential energy. In the figure given below, there is a huge plate that is negatively charged, and it has some positive charges stuck on it. 

In the figure, when positive charges are separated from the negatively charged plate, they experience force. So, to separate out the charges from the places, work needs to be done against the force that is acting on them. In this process, potential energy is stored in them. When these charges are released, they start running towards the negatively charged plate. So, in this situation, the potential energy stored in these charges is converted into kinetic energy. 

For a two-charge system with charges q and Q given in the figure above, the change in electric potential energy in taking the charge q, from A to B is given by, 

W_{AB}=\frac{Qq}{4 \pi \epsilon}(\frac{1}{r_B} - \frac{1}{r_A})

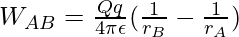
Electric Potential 

Electric potential is defined as the difference in the potential energy per unit charge between two places. To check the difference in the electric potential between two positions under the influence of an electric field, it is asked, how much the potential energy of a unit positive charge will change if that charge is moved from this position to the other position. Is denoted by V, 

V = 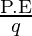\frac{\text{P.E}}{q}

In a similar situation as described in the previous section. The positive charge is near the plate, the farther the charge is from this plate, the more the work done on the charge. So, in this case, we say that the potential near the negatively charged plate is low and as one goes far the potential increases. Now let’s understand the potential due to a point charge in formal terms. 

Electric Potential Due to Point Charge

Consider a point charge as shown in the figure below. Notice that in the figure, there are some concentric circles. These concentric circles represent the equipotential contour. That means, that at all the points in a single contour. The potential is the same. The goal is to calculate the electric potential due to this point charge between two points A and B. 

Electric potential difference is also called voltage, and it is measured in the units of Volts. 

voltageAB = electric potential differenceAB = 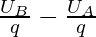\frac{U_B}{q} - \frac{U_A}{q}  

The potential up until now has been defined as a difference; a formulation in terms of absolute potential is required. The above formulation will be modified to come up with this new definition. At infinite, the electric field and the potential are assumed to be zero. Now, the potential at every point will be calculated with respect to the infinite, and it will give an absolute value of the potential. 

Now, rB = 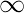\infty and rA

voltageAB = 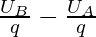\frac{U_B}{q} - \frac{U_A}{q}  

                  = \frac{1}{4\pi \epsilon }\frac{q}{r_A} - \frac{1}{4\pi \epsilon }\frac{q}{r_B}

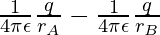
Now, rB = 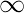\infty

              = \frac{1}{4\pi \epsilon }\frac{q}{r_A} - \frac{1}{4\pi \epsilon }\frac{q}{\infty}

              = \frac{1}{4\pi \epsilon }\frac{q}{r_A}

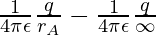
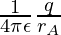
Superposition of Electric Potential 

For a system of point charges, the total potential at a point is given by the algebraic sum of the potential for individual charges at that point. For example, in a system containing charges Q1, Q2, and Q3 at a distance of r1, r2, and r3 from a point. Then, the potential at this point will be given by the following equation, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

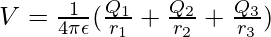
Sample Problems

Question 1: Find the potential at a distance of 1 m due to a charge of 2pC. 

Answer: 

The potential due to a point charge is given by, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

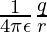
Here, q = 2 pC = 2 x 10-12C and r = 1 m. 

Plugging the values into this equation, 

V = 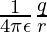\frac{1}{4\pi \epsilon }\frac{q}{r}

⇒ V = 9 \times 10^{9} .\frac{2 \times 10^{-12}}{1}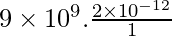

⇒ V= 9 × 109 × 2 x 10-12

⇒ V= 18 × 10-3

Question 2: Find the potential at a distance of 0.5 m due to a charge of 10pC. 

Answer: 

The potential due to a point charge is given by, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

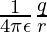
Here, q = 10 pC = 10 x 10-12C and r = 0.5m. 

Plugging the values into this equation, 

V = 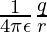\frac{1}{4\pi \epsilon }\frac{q}{r}

⇒ V = 9 \times 10^{9} .\frac{10 \times 10^{-12}}{0.5}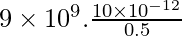

⇒ V= 9 × 109 × 2 x 10-11

⇒ V= 18 x 10-2

Question 3: Find the potential energy at a distance of 0.5 m due to a charge of 10pC and -10pC. 

Answer: 

The potential due to a point charge is given by, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

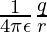
Here, q1 = 10 pC = 10 x 10-12C, q2 = -10 pC = -10 x 10-12C and r = 0.5m. 

Since there are two charges in the system, the total potential will be given by the superposition equation. 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

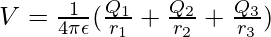
For two charges, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} )

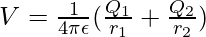
Plugging the values into this equation, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} ) \\ = V = 9 \times 10^9(\frac{10 \times 10^{-12}}{0.5} - \frac{10 \times 10^{-12}}{0.5)}

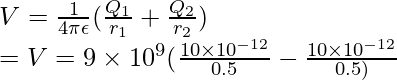
⇒ V= 0

Question 4: Find the potential energy at a distance of 2 m due to a charge of 10pC and -2pC. 

Answer: 

The potential due to a point charge is given by, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

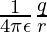
Here, q1 = 10 pC = 10 x 10-12C, q2 = -10 pC = -2 x 10-12C and r = 2 m. 

Since there are two charges in the system, the total potential will be given by the superposition equation. 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

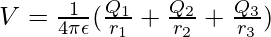
For two charges, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} )

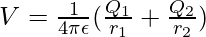
Plugging the values into this equation, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} ) \\ = V = 9 \times 10^9(\frac{10 \times 10^{-12}}{2} - \frac{2 \times 10^{-12}}{2}) \\ = V = 9 \times 10^9(4 \times 10^{-12}) \\ = V = 36 \times 10^{-3}

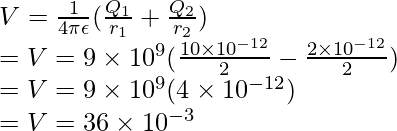
⇒ V= 36 × 10-3 V

Question 5: Two charges are kept at opposite corners of rectangles as shown in the figure. Find the potential at the corner between them. 

Answer: 

The potential due to a point charge is given by, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

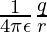
Here, q1 = 1 pC = 10-12C, q2 = -2 pC = -2 x 10-12C and r1 = 2 m and r2 = 1 m. 

Since there are two charges in the system, the total potential will be given by the superposition equation. 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

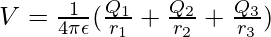
For two charges, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} )

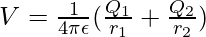
Plugging the values into this equation, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} ) \\ = V = 9 \times 10^9(\frac{10^{-12}}{2} - \frac{2 \times 10^{-12}}{1}) \\ = V = 9 \times 10^9((-3.5) \times 10^{-12}) \\ = V = -31.5 \times 10^{-3} \text{ V}

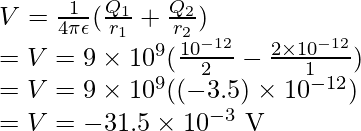
⇒ V= 36 × 10-3 V



Like Article
Suggest improvement
Previous
Electric Potential Energy
Next
Electric Potential Due to System of Charges
Share your thoughts in the comments

Similar Reads

Electric Charge and Electric Field - Electric Flux, Coulomb's Law, Sample Problems
Electric Field due to a Point Charge
Electric Potential Due to System of Charges
Difference Between Electric Potential and Potential Difference
Basic Properties of Electric Charge
Electric Charge
Dimensions of Electric Charge
Electric Charge Formula
Unit of Electric Charge
Electric Field due to Infinitely Long Straight Wire

A
anjalishukla1859
Article Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox