Electric charge is a fundamental property of matter that controls how an electric or magnetic field affects elementary particles. Electric charge exists in discrete natural units that cannot be generated or destroyed. Positive and negative charges are the two types of electric charges. When two items with an excess of one type of charge are near enough together, they repel each other. When two positively charged and negatively charged objects are in close contact, they attract one other.
Many fundamental, or subatomic, particles of material share the property of electric charge. Protons have a positive charge, whereas electrons have a negative charge. Neutrons, on the other hand, are uncharged or neutral particles. The negative charge of each electron and the positive charge of each proton have the same magnitude, according to experiments. The charge of an electron or proton, which is a fundamental physical constant, is measured in natural units.
Electric field due to a point charge
Consider a point charge Q at the origin O, which is placed in a vacuum. Coulomb’s law states that if another point charge q is placed at a position P where OP = r, the charge Q will exert a force on q. The charge Q generates an electric field that extends throughout the environment. When a new charge, q, is introduced at point P, the field there acts on it and generates a force. The electric field produced by a charge Q at a location r can be expressed as,
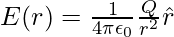
where r = r/r is a unit vector from the origin to the point r. As a result, the above expression specifies the electric field value for each value of the position vector r. The term “field” refers to how some distributed quantity (which could be a scalar or a vector) varies with position. The electric field’s existence has been combined with the charge’s effect. The force F exerted by a charge Q on a charge q is calculated as


Electric field (a) due to a charge Q, (b) due to a charge –Q.
It’s worth noting that the charge q has an equal and opposing force on the charge Q.
The electrostatic force between charges Q and q can be viewed as an interaction between charge q and Q’s electric field, and vice versa. The charge q feels a force F equal to the charge q multiplied by the electric field E at the location of q if its position is denoted by the vector r.
Therefore,
F(r) = q E(r)
The SI unit of the electric field as N/C.
Here are a few key points to consider:
- The electric field produced by a charge Q is numerically equivalent to the force exerted by it if q is unity. As a result, the electric field produced by a charge Q at a given location in space can be described as the force that a unit positive charge would experience if it were placed there. The charge Q that generates the electric field is known as a source charge, whereas the charge q that measures the effect of a source charge is known as a test charge. It’s important to keep in mind that the source charge Q must remain in its original place. However, if a charge q is applied to any location around Q, Q will be subjected to an electrical force as a result of q and will begin to move. Making q negligibly tiny is one approach to get around this problem. The force F is therefore negligibly small, but the ratio F/q is finite, and the electric field is defined as follows:
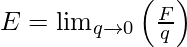
- It’s worth noting that the electric field E caused by Q is independent of q, despite the fact that it’s operationally described in terms of some test charge q. This is due to the fact that F is proportional to q, hence the F/q ratio is independent of q. The force F exerted on the charge q by the charge Q is determined by the charge q’s specific location, which can be any value in the region surrounding the charge Q. As a result, the electric field E produced by Q is likewise affected by the spatial coordinate r. We receive varied values of electric field E for different places of the charge q across space. Every point in three-dimensional space contains the field.
- The electric field from a positive charge will radiate outwards. If the source charge is negative, on the other hand, the electric field vector at each point points inwards radially.
- Because the amount of the force F on charge q owing to charge Q is solely determined by the charge q’s distance r from charge Q, the magnitude of the electric field E is also solely determined by the distance r. As a result, the size of the charge Q’s electric field E is the same at equal distances from it. On a sphere with the point charge at its center, the magnitude of the electric field E owing to a point charge is thus the same; in other words, it possesses spherical symmetry.
Electric field due to a system of charges

The electric field at a point due to a system of charges is the vector sum of the electric fields at the point due to individual charges.
Consider a system of charges q1, q2,…, qn with position vectors r1, r2,…, rn with respect to some origin O. The force experienced by a unit test charge placed at that point, without altering the original positions of charges q1, q2,…, qn, is described as the electric field at a point in space owing to a system of charges, similar to the electric field at a point in space due to a single charge. To determine this field at a location P represented by position vector r, we can apply Coulomb’s law and the superposition principle.
Electric field E1 at r due to q1 at r1 can be written as,
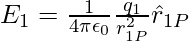
where 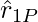 is a unit vector in the direction from q1 to P, and r1P is the distance between q1 and P.
is a unit vector in the direction from q1 to P, and r1P is the distance between q1 and P.
Similarly, electric field E2 at r due to q2 at r2 can be expressed as,
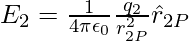
where 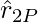 is a unit vector in the direction from q2 to P and r2P is the distance between q2 and P. Similar expressions for fields E3 , E4, …, En due to charges q3 , q4 , …, qn . By the superposition principle, the electric field E at r due to the system of charges can be expressed as,
is a unit vector in the direction from q2 to P and r2P is the distance between q2 and P. Similar expressions for fields E3 , E4, …, En due to charges q3 , q4 , …, qn . By the superposition principle, the electric field E at r due to the system of charges can be expressed as,
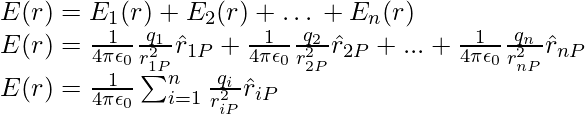
E is a vector variable that varies from one location in space to another and is determined by the source charge positions.
Physical significance of the electric field
The concept of the electric field is useful in electrostatics, but it isn’t absolutely necessary. An elegant approach to describing the electrical environment of a system of charges is to use the term electric field.
The force a unit positive test charge would experience if put at a position in the space around a system of charges (without upsetting the system) is determined by the electric field at that point. The electric field is a property of the system of charges, and it is unrelated to the test charge used to calculate the field. In physics, a field is a quantity that is defined at every point in space and can vary from one point to the next. Because force is a vector quantity, the electric field is a vector field.
However, when we move beyond electrostatics and consider time-dependent electromagnetic events, the actual physical relevance of the concept of electric field appears. Consider the force between two distant charges in accelerated motion, q1, and q2. The speed at which a signal or information may travel from one location to another is now equal to c, the speed of light. As a result, any motion of q1, on q2 cannot have an instantaneous effect. Between the effect (force on q2) and the cause (motion of q1), there will be a temporal delay. The concept of electric field (strictly, electromagnetic field) is intuitive and extremely useful in this context. The field image is as follows: the accelerated motion of charge q1 generates electromagnetic waves, which propagate at c, reach q2, and exert a force on q2. The time delay is elegantly explained by the concept of field. Despite the fact that electric and magnetic fields can only be identified by their effects (forces) on charges, they are considered physical things rather than mathematical abstractions. They have their own dynamics, i.e., they evolve according to their own set of rules. They are also capable of transporting energy. Thus, a source of time-dependent electromagnetic fields that are turned on for a short time and then turned off leaves propagating electromagnetic fields that transport energy behind. Faraday was the first to establish the concept of field, and it is today one of the most important concepts in physics.
Sample Problems
Problem 1: Two particles with charges +4 μC and -9 μC are kept fixed at a separation of 20 cm from each other. Locate the point at which the resultant electric field due to the system of two point charges is zero.
Solution:
The null point is the point at which the resultant electric field owing to the given system of point charges is zero. We know that in a system with two point charges, the null point is on the line connecting the two charges, and that the null point is always closer to the lower magnitude charge. The null point will not be in the space between the charges since the two charges are of opposite nature.

Assume that the electric field at point P is zero. The point P is at a distance of x from the +4C charge. The field vanishes at point P, hence the magnitudes of the separate fields produced by the two point charges at P must be equal (and directions anti-parallel).

Because there is no chance of a null point in the region between the two charges, the negative value of x should be ignored. As a result, the electric field’s zero point is located on the line connecting the two point charges, 40 cm to the left of the positively charged particle.
Problem 2: A point charge -2μC is located at point A(2,2,2), then find the electric field strength vector at point B(1,1,1).
Solution:
Electric field intensity vector due to a point charge q at a position r can be expressed as,
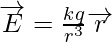
The position vector of the point of calculation of the electric field with regard to the location point of the source point charge is r, and the proper sign is q.

Therefore, electric field at point B is
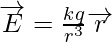
Substitute the value in the above formula,
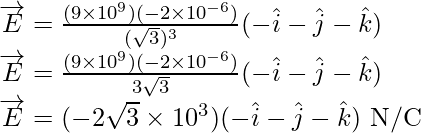
Problem 3: What is the force between two small charged spheres having charges of 2 x 10-7 C and 3 x 10-7 C placed 30 cm apart in the air?
Solution:
Given,
The magnitude of repulsive force is 6 × 10-3 N.
Charge on the first sphere, q1 is 2 × 10-7 C.
Charge on the second sphere, q2 is 3 × 10-7 C.
Distance between the spheres, r is 30 cm i.e. 0.3 m.
The expression for the electrostatic force between the spheres can be written as,
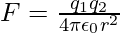
Substitute the value in the above formula,
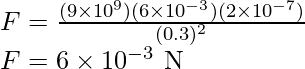
Therefore, force between the two small charged spheres is 6 × 10–3 N. The charges are of same nature. Hence, force between them will be repulsive.
Problem 4: Explain the meaning of the statement ‘electric charge of a body is quantized’.
Solution:
A body’s electric charge is quantized. This means that only an integral number of electrons (1, 2,…, n) can be transported from one substance to another. The transfer of charges is not fractional. As a result, a body can only have total charge in integral multiples of electric charge.
The charges used in macroscopic or large-scale charges are enormous in comparison to the magnitude of electric charge. As a result, on a macroscopic scale, quantization of electric charge is useless. As a result, it is overlooked, and it is assumed that electric charge is constant.
Problem 5: When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Solution:
Because charges are formed in pairs, rubbing produces charges of equal magnitude but opposing nature on the two bodies. Charging by friction is the name for this type of charging. The system of two rubbed bodies has a net charge of zero. This is due to the fact that equal amounts of opposite charges cancel each other out. When rubbing a silk cloth over a glass rod, opposite natured charges develop on both bodies. These phenomena are in accordance with the law of energy conservation. Many other pairs of bodies exhibit a similar phenomena.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...