Eigenvector Centrality (Centrality Measure)

Difficulty Level : Medium
Last Updated : 12 Feb, 2018

In graph theory, eigenvector centrality (also called eigencentrality) is a measure of the influence of a node in a network. It assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes.

Google’s PageRank and the Katz centrality are variants of the eigenvector centrality.

Using the adjacency matrix to find eigenvector centrality

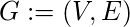
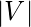
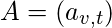
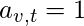
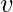
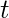
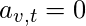
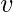
For a given graph $G:=(V,E)$ with $|V|$ vertices let $A = (a_{v,t})$ be the adjacency matrix, i.e. $a_{v,t} = 1$ if vertex $v$ is linked to vertex $t$ , and $a_{v,t} = 0$ otherwise. The relative centrality score of vertex $v$ can be defined as:

$x_{v}={\frac {1}{\lambda }}\sum _{t\in M(v)}x_{t}={\frac {1}{\lambda }}\sum _{t\in G}a_{v,t}x_{t}$
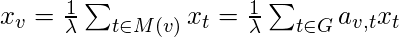
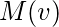
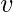
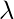
where $M(v)$ is a set of the neighbors of $v$ and $\lambda$ is a constant. With a small rearrangement this can be rewritten in vector notation as the eigenvector equation

$\mathbf {Ax} =\lambda \mathbf {x}$
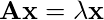
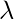
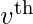
In general, there will be many different eigenvalues $\lambda$ for which a non-zero eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be non-negative implies (by the Perron–Frobenius theorem) that only the greatest eigenvalue results in the desired centrality measure. 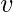The $v^{\text{th}}$ component of the related eigenvector then gives the relative centrality score of the vertex $v$ in the network. The eigenvector is only defined up to a common factor, so only the ratios of the centralities of the vertices are well defined. To define an absolute score one must normalise the eigen vector e.g. such that the sum over all vertices is 1 or the total number of vertices n. Power iteration is one of many eigenvalue algorithms that may be used to find this dominant eigenvector. Furthermore, this can be generalized so that the entries in A can be real numbers representing connection strengths, as in a stochastic matrix.

Following is the code for the calculation of the Eigen Vector Centrality of the graph and its various nodes.

def eigenvector_centrality(G, max_iter=100, tol=1.0e-6, nstart=None,
                           weight='weight'):
    """Compute the eigenvector centrality for the graph G.
  
    Eigenvector centrality computes the centrality for a node based on the
    centrality of its neighbors. The eigenvector centrality for node `i` is
  
    .. math::
  
        \mathbf{Ax} = \lambda \mathbf{x}
  
    where `A` is the adjacency matrix of the graph G with eigenvalue `\lambda`.
    By virtue of the Perron–Frobenius theorem, there is a unique and positive
    solution if `\lambda` is the largest eigenvalue associated with the
    eigenvector of the adjacency matrix `A` ([2]_).
  
    Parameters
    ----------
    G : graph
      A networkx graph
  
    max_iter : integer, optional
      Maximum number of iterations in power method.
  
    tol : float, optional
      Error tolerance used to check convergence in power method iteration.
  
    nstart : dictionary, optional
      Starting value of eigenvector iteration for each node.
  
    weight : None or string, optional
      If None, all edge weights are considered equal.
      Otherwise holds the name of the edge attribute used as weight.
  
    Returns
    -------
    nodes : dictionary
       Dictionary of nodes with eigenvector centrality as the value.
  
        
    Notes
    ------
    The eigenvector calculation is done by the power iteration method and has
    no guarantee of convergence. The iteration will stop after ``max_iter``
    iterations or an error tolerance of ``number_of_nodes(G)*tol`` has been
    reached.
  
    For directed graphs this is "left" eigenvector centrality which corresponds
    to the in-edges in the graph. For out-edges eigenvector centrality
    first reverse the graph with ``G.reverse()``.
  
     
    """
    from math import sqrt
    if type(G) == nx.MultiGraph or type(G) == nx.MultiDiGraph:
        raise nx.NetworkXException("Not defined for multigraphs.")
  
    if len(G) == 0:
        raise nx.NetworkXException("Empty graph.")
  
    if nstart is None:
  
        # choose starting vector with entries of 1/len(G)
        x = dict([(n,1.0/len(G)) for n in G])
    else:
        x = nstart
  
    # normalize starting vector
    s = 1.0/sum(x.values())
    for k in x:
        x[k] *= s
    nnodes = G.number_of_nodes()
  
    # make up to max_iter iterations
    for i in range(max_iter):
        xlast = x
        x = dict.fromkeys(xlast, 0)
  
        # do the multiplication y^T = x^T A
        for n in x:
            for nbr in G[n]:
                x[nbr] += xlast[n] * G[n][nbr].get(weight, 1)
  
        # normalize vector
        try:
            s = 1.0/sqrt(sum(v**2 for v in x.values()))
  
        # this should never be zero?
        except ZeroDivisionError:
            s = 1.0
        for n in x:
            x[n] *= s
  
        # check convergence
        err = sum([abs(x[n]-xlast[n]) for n in x])
        if err < nnodes*tol:
            return x
  
    raise nx.NetworkXError("""eigenvector_centrality():
power iteration failed to converge in %d iterations."%(i+1))""")

The above function is invoked using the networkx library and once the library is installed, you can eventually use it and the following code has to be written in python for the implementation of the eigen vector centrality of a node.

>>> import networkx as nx
>>> G = nx.path_graph(4)
>>> centrality = nx.eigenvector_centrality(G)
>>> print(['%s %0.2f'%(node,centrality[node]) for node in centrality])

The output of the above code is:

['0 0.37', '1 0.60', '2 0.60', '3 0.37']

The above result is a dictionary depicting the value of eigen vector centrality of each node. The above is an extension of my article series on the centrality measures. Keep networking!!!

References
You can read more about the same at

https://en.wikipedia.org/wiki/Eigenvector_centrality

http://networkx.readthedocs.io/en/networkx-1.10/index.html

Image Source
https://image.slidesharecdn.com/srspesceesposito-150425073726-conversion-gate01/95/network-centrality-measures-and-their-effectiveness-28-638.jpg?cb=1429948092

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

My Personal Notes

Related Articles