Eigenvalues and Eigenvectors in MATLAB
Last Updated :
20 Nov, 2021
Eigenvalues and Eigenvectors are properties of a square matrix.
Let ![Rendered by QuickLaTeX.com A =[a_{ij}]_{N*N}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-328a66cda703fe48aaafc0f9991c319b_l3.png) is an N*N matrix, X be a vector of size N*1 and
is an N*N matrix, X be a vector of size N*1 and 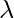 be a scalar.
be a scalar.
Then the values X,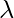 satisfying the equation
satisfying the equation 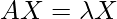 are eigenvectors and eigenvalues of matrix A respectively.
are eigenvectors and eigenvalues of matrix A respectively.
- A matrix of size N*N possess N eigenvalues
- Every eigenvalue corresponds to an eigenvector.
Matlab allows the users to find eigenvalues and eigenvectors of matrix using eig() method. Different syntaxes of eig() method are:
- e = eig(A)
- [V,D] = eig(A)
- [V,D,W] = eig(A)
- e = eig(A,B)
Let us discuss the above syntaxes in detail:
e = eig(A)
- It returns the vector of eigenvalues of square matrix A.
Matlab
A = [0 1 2;
1 0 -1;
2 -1 0];
disp("Matrix");
disp(A);
e = eig(A);
disp("Eigenvalues");
disp(e);
|
Output :

[V,D] = eig(A)
- It returns the diagonal matrix D having diagonals as eigenvalues.
- It also returns the matrix of right vectors as V.
- Normal eigenvectors are termed as right eigenvectors.
- V is a collection of N eigenvectors of each N*1 size(A is N*N size) that satisfies A*V = V*D
Matlab
A = [8 -6 2;
-6 7 -4;
2 -4 3];
disp("Matrix");
disp(A);
[V,D] = eig(A);
disp("Diagonal matrix of Eigenvalues");
disp(D);
disp("Right eigenvectors")
disp(V);
|
Output :

[V,D,W] = eig(A)
- Along with the diagonal matrix of eigenvalues D and right eigenvectors V, it also returns the left eigenvectors of matrix A.
- A left eigenvector u is a 1*N matrix that satisfies the equation u*A = k*u, where k is a left eigenvalue of matrix A.
- W is the collection of N left eigenvectors of A that satisfies W’*A = D*W’.
Matlab
A = [10 -6 2;
-6 7 -4;
2 -4 3];
disp("Matrix :");
disp(A);
[V,D,W] = eig(A);
disp("Diagonal matrix of Eigenvalues :");
disp(D);
disp("Right eigenvectors :")
disp(V);
disp("Left eigenvectors :")
disp(W);
|
Output :

e = eig(A,B)
- It returns the generalized eigenvalues of two square matrices A and B of the same size.
- A generalized eigenvalue λ and a corresponding eigenvector v satisfy Av=λBv.
Matlab
A = [10 -6 2;
-6 7 -4;
2 -4 3];
B = [8 6 1;
6 17 2;
-1 4 3];
disp("Matrix A:");
disp(A);
disp("Matrix B:");
disp(B);
e = eig(A,B);
disp("Generalized eigenvalues :")
disp(e);
|
Output :

Share your thoughts in the comments
Please Login to comment...