Eigenspace and Eigenspectrum Values in a Matrix
Last Updated :
15 Jan, 2020
Prerequisites:
For a given matrix
A the set of all eigenvectors of
A associated with an eigenvalue
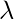
spans a subspace, which is called the
Eigenspace of
A with respect to
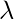
and is denoted by
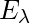
. The set of all eigenvalues of
A is called
Eigenspectrum, or just spectrum, of
A.
If
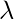
is an eigenvalue of A, then the corresponding eigenspace
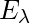
is the solution space of the homogeneous system of linear equations
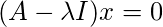
. Geometrically, the eigenvector corresponding to a non – zero eigenvalue points in a direction that is stretched by the linear mapping. The eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, then the direction of the stretching is flipped.
Below are some useful properties of eigenvalues and eigenvectors in addition to the properties which are already listed in the article
Mathematics | Eigen Values and Eigen Vectors.
A matrix A and its transpose 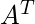 possess the same eigenvalues but not necessarily the same eigenvectors.
The eigenspace
possess the same eigenvalues but not necessarily the same eigenvectors.
The eigenspace 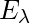 is the null space of
is the null space of 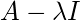 since
since
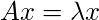
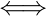
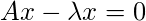
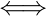
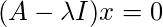
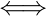
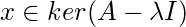 Note:
Note: ker stands for
Kernel which is another name for
null space.
Computing Eigenvalues, Eigenvectors, and Eigenspaces:
Consider given 2 X 2 matrix:
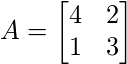 Step 1: Characteristic polynomial and Eigenvalues.
The characteristic polynomial is given by
det(
Step 1: Characteristic polynomial and Eigenvalues.
The characteristic polynomial is given by
det(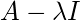 )
)
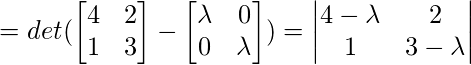
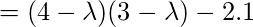 After we factorize the characteristic polynomial, we will get
After we factorize the characteristic polynomial, we will get
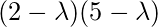 which gives eigenvalues as
which gives eigenvalues as 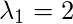 and
and 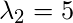 Step 2: Eigenvectors and Eigenspaces
We find the eigenvectors that correspond to these eigenvalues by looking
at vectors x such that
Step 2: Eigenvectors and Eigenspaces
We find the eigenvectors that correspond to these eigenvalues by looking
at vectors x such that
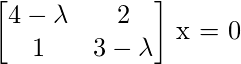 For
For 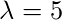 we obtain
we obtain
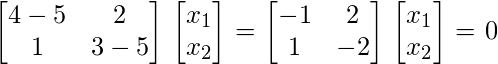 After solving the above homogeneous system of equations,
we will obtain a solution space
After solving the above homogeneous system of equations,
we will obtain a solution space
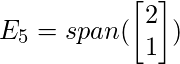 This eigenspace is one dimensional as it possesses a single basis vector.
Similarly, we find eigenvector for
This eigenspace is one dimensional as it possesses a single basis vector.
Similarly, we find eigenvector for 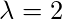 by solving
the homogeneous system of equations
by solving
the homogeneous system of equations
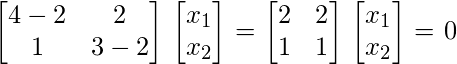 This means any vector
This means any vector 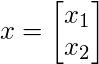 , where
, where 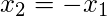 such as
such as  is an eigenvector with
eigenvalue 2. This means eigenspace is given as
is an eigenvector with
eigenvalue 2. This means eigenspace is given as
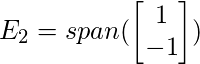
The two eigenspaces
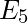
and
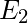
in the above example are one dimensional as they are each spanned by a single vector. However, in other cases, we may have multiple identical eigenvectors and the eigenspaces may have more than one dimension.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...