Optimal Binary Search Tree | DP-24
Last Updated :
10 Jul, 2023
An Optimal Binary Search Tree (OBST), also known as a Weighted Binary Search Tree, is a binary search tree that minimizes the expected search cost. In a binary search tree, the search cost is the number of comparisons required to search for a given key.
In an OBST, each node is assigned a weight that represents the probability of the key being searched for. The sum of all the weights in the tree is 1.0. The expected search cost of a node is the sum of the product of its depth and weight, and the expected search cost of its children.
To construct an OBST, we start with a sorted list of keys and their probabilities. We then build a table that contains the expected search cost for all possible sub-trees of the original list. We can use dynamic programming to fill in this table efficiently. Finally, we use this table to construct the OBST.
The time complexity of constructing an OBST is O(n^3), where n is the number of keys. However, with some optimizations, we can reduce the time complexity to O(n^2). Once the OBST is constructed, the time complexity of searching for a key is O(log n), the same as for a regular binary search tree.
The OBST is a useful data structure in applications where the keys have different probabilities of being searched for. It can be used to improve the efficiency of searching and retrieval operations in databases, compilers, and other computer programs.
Given a sorted array key [0.. n-1] of search keys and an array freq[0.. n-1] of frequency counts, where freq[i] is the number of searches for keys[i]. Construct a binary search tree of all keys such that the total cost of all the searches is as small as possible.
Let us first define the cost of a BST. The cost of a BST node is the level of that node multiplied by its frequency. The level of the root is 1.
Examples:
Input: keys[] = {10, 12}, freq[] = {34, 50}
There can be following two possible BSTs
10 12
\ /
12 10
I II
Frequency of searches of 10 and 12 are 34 and 50 respectively.
The cost of tree I is 34*1 + 50*2 = 134
The cost of tree II is 50*1 + 34*2 = 118
Input: keys[] = {10, 12, 20}, freq[] = {34, 8, 50}
There can be following possible BSTs
10 12 20 10 20
\ / \ / \ /
12 10 20 12 20 10
\ / / \
20 10 12 12
I II III IV V
Among all possible BSTs, cost of the fifth BST is minimum.
Cost of the fifth BST is 1*50 + 2*34 + 3*8 = 142
1) Optimal Substructure:
The optimal cost for freq[i..j] can be recursively calculated using the following formula.
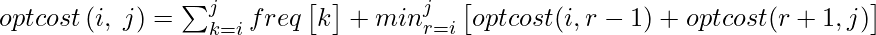
We need to calculate optCost(0, n-1) to find the result.
The idea of above formula is simple, we one by one try all nodes as root (r varies from i to j in second term). When we make rth node as root, we recursively calculate optimal cost from i to r-1 and r+1 to j.
We add sum of frequencies from i to j (see first term in the above formula)
The reason for adding the sum of frequencies from i to j:
This can be divided into 2 parts one is the freq[r]+sum of frequencies of all elements from i to j except r. The term freq[r] is added because it is going to be root and that means level of 1, so freq[r]*1=freq[r]. Now the actual part comes, we are adding the frequencies of remaining elements because as we take r as root then all the elements other than that are going 1 level down than that is calculated in the subproblem. Let me put it in a more clear way, for calculating optcost(i,j) we assume that the r is taken as root and calculate min of opt(i,r-1)+opt(r+1,j) for all i<=r<=j. Here for every subproblem we are choosing one node as a root. But in reality the level of subproblem root and all its descendant nodes will be 1 greater than the level of the parent problem root. Therefore the frequency of all the nodes except r should be added which accounts to the descend in their level compared to level assumed in subproblem.
2) Overlapping Subproblems
Following is recursive implementation that simply follows the recursive structure mentioned above.
C++
#include <bits/stdc++.h>
using namespace std;
int sum(int freq[], int i, int j);
int optCost(int freq[], int i, int j)
{
if (j < i)
return 0;
if (j == i)
return freq[i];
int fsum = sum(freq, i, j);
int min = INT_MAX;
for (int r = i; r <= j; ++r)
{
int cost = optCost(freq, i, r - 1) +
optCost(freq, r + 1, j);
if (cost < min)
min = cost;
}
return min + fsum;
}
int optimalSearchTree(int keys[],
int freq[], int n)
{
return optCost(freq, 0, n - 1);
}
int sum(int freq[], int i, int j)
{
int s = 0;
for (int k = i; k <= j; k++)
s += freq[k];
return s;
}
int main()
{
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = sizeof(keys) / sizeof(keys[0]);
cout << "Cost of Optimal BST is "
<< optimalSearchTree(keys, freq, n);
return 0;
}
|
Java
public class GFG
{
static int optCost(int freq[], int i, int j)
{
if (j < i)
return 0;
if (j == i)
return freq[i];
int fsum = sum(freq, i, j);
int min = Integer.MAX_VALUE;
for (int r = i; r <= j; ++r)
{
int cost = optCost(freq, i, r-1) +
optCost(freq, r+1, j);
if (cost < min)
min = cost;
}
return min + fsum;
}
static int optimalSearchTree(int keys[], int freq[], int n)
{
return optCost(freq, 0, n-1);
}
static int sum(int freq[], int i, int j)
{
int s = 0;
for (int k = i; k <=j; k++)
s += freq[k];
return s;
}
public static void main(String[] args) {
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = keys.length;
System.out.println("Cost of Optimal BST is " +
optimalSearchTree(keys, freq, n));
}
}
|
Python3
def optCost(freq, i, j):
if j < i:
return 0
if j == i:
return freq[i]
fsum = Sum(freq, i, j)
Min = 999999999999
for r in range(i, j + 1):
cost = (optCost(freq, i, r - 1) +
optCost(freq, r + 1, j))
if cost < Min:
Min = cost
return Min + fsum
def optimalSearchTree(keys, freq, n):
return optCost(freq, 0, n - 1)
def Sum(freq, i, j):
s = 0
for k in range(i, j + 1):
s += freq[k]
return s
if __name__ == '__main__':
keys = [10, 12, 20]
freq = [34, 8, 50]
n = len(keys)
print("Cost of Optimal BST is",
optimalSearchTree(keys, freq, n))
|
C#
using System;
class GFG
{
static int optCost(int []freq, int i, int j)
{
if (j < i)
return 0;
if (j == i)
return freq[i];
int fsum = sum(freq, i, j);
int min = int.MaxValue;
for (int r = i; r <= j; ++r)
{
int cost = optCost(freq, i, r-1) +
optCost(freq, r+1, j);
if (cost < min)
min = cost;
}
return min + fsum;
}
static int optimalSearchTree(int []keys, int []freq, int n)
{
return optCost(freq, 0, n-1);
}
static int sum(int []freq, int i, int j)
{
int s = 0;
for (int k = i; k <=j; k++)
s += freq[k];
return s;
}
public static void Main()
{
int []keys = {10, 12, 20};
int []freq = {34, 8, 50};
int n = keys.Length;
Console.Write("Cost of Optimal BST is " +
optimalSearchTree(keys, freq, n));
}
}
|
Javascript
<script>
function optCost(freq, i, j)
{
if (j < i)
return 0;
if (j == i)
return freq[i];
var fsum = sum(freq, i, j);
var min = Number. MAX_SAFE_INTEGER;
for (var r = i; r <= j; ++r)
{
var cost = optCost(freq, i, r - 1) +
optCost(freq, r + 1, j);
if (cost < min)
min = cost;
}
return min + fsum;
}
function optimalSearchTree(keys, freq, n)
{
return optCost(freq, 0, n - 1);
}
function sum(freq, i, j)
{
var s = 0;
for (var k = i; k <= j; k++)
s += freq[k];
return s;
}
var keys = [10, 12, 20];
var freq = [34, 8, 50];
var n = keys.length;
document.write("Cost of Optimal BST is " +
optimalSearchTree(keys, freq, n));
</script>
|
C
#include <stdio.h>
#include <limits.h>
int sum(int freq[], int i, int j);
int optCost(int freq[], int i, int j)
{
if (j < i)
return 0;
if (j == i)
return freq[i];
int fsum = sum(freq, i, j);
int min = INT_MAX;
for (int r = i; r <= j; ++r)
{
int cost = optCost(freq, i, r-1) +
optCost(freq, r+1, j);
if (cost < min)
min = cost;
}
return min + fsum;
}
int optimalSearchTree(int keys[], int freq[], int n)
{
return optCost(freq, 0, n-1);
}
int sum(int freq[], int i, int j)
{
int s = 0;
for (int k = i; k <=j; k++)
s += freq[k];
return s;
}
int main()
{
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = sizeof(keys)/sizeof(keys[0]);
printf("Cost of Optimal BST is %d ",
optimalSearchTree(keys, freq, n));
return 0;
}
|
OutputCost of Optimal BST is 142
Time complexity of the above naive recursive approach is exponential. It should be noted that the above function computes the same subproblems again and again. We can see many subproblems being repeated in the following recursion tree for freq[1..4].

Since same subproblems are called again, this problem has Overlapping Subproblems property. So optimal BST problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of same subproblems can be avoided by constructing a temporary array cost[][] in bottom up manner.
Dynamic Programming Solution
Following is C/C++ implementation for optimal BST problem using Dynamic Programming. We use an auxiliary array cost[n][n] to store the solutions of subproblems. cost[0][n-1] will hold the final result. The challenge in implementation is, all diagonal values must be filled first, then the values which lie on the line just above the diagonal. In other words, we must first fill all cost[i][i] values, then all cost[i][i+1] values, then all cost[i][i+2] values. So how to fill the 2D array in such manner> The idea used in the implementation is same as Matrix Chain Multiplication problem, we use a variable ‘L’ for chain length and increment ‘L’, one by one. We calculate column number ‘j’ using the values of ‘i’ and ‘L’.
C++
#include <bits/stdc++.h>
using namespace std;
int sum(int freq[], int i, int j);
int optimalSearchTree(int keys[], int freq[], int n)
{
int cost[n][n];
for (int i = 0; i < n; i++)
cost[i][i] = freq[i];
for (int L = 2; L <= n; L++)
{
for (int i = 0; i <= n-L+1; i++)
{
int j = i+L-1;
cost[i][j] = INT_MAX;
int off_set_sum = sum(freq, i, j);
for (int r = i; r <= j; r++)
{
int c = ((r > i)? cost[i][r-1]:0) +
((r < j)? cost[r+1][j]:0) +
off_set_sum;
if (c < cost[i][j])
cost[i][j] = c;
}
}
}
return cost[0][n-1];
}
int sum(int freq[], int i, int j)
{
int s = 0;
for (int k = i; k <= j; k++)
s += freq[k];
return s;
}
int main()
{
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = sizeof(keys)/sizeof(keys[0]);
cout << "Cost of Optimal BST is " << optimalSearchTree(keys, freq, n);
return 0;
}
|
C
#include <stdio.h>
#include <limits.h>
int sum(int freq[], int i, int j);
int optimalSearchTree(int keys[], int freq[], int n)
{
int cost[n][n];
for (int i = 0; i < n; i++)
cost[i][i] = freq[i];
for (int L=2; L<=n; L++)
{
for (int i=0; i<=n-L+1; i++)
{
int j = i+L-1;
int off_set_sum = sum(freq, i, j);
cost[i][j] = INT_MAX;
for (int r=i; r<=j; r++)
{
int c = ((r > i)? cost[i][r-1]:0) +
((r < j)? cost[r+1][j]:0) +
off_set_sum;
if (c < cost[i][j])
cost[i][j] = c;
}
}
}
return cost[0][n-1];
}
int sum(int freq[], int i, int j)
{
int s = 0;
for (int k = i; k <=j; k++)
s += freq[k];
return s;
}
int main()
{
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = sizeof(keys)/sizeof(keys[0]);
printf("Cost of Optimal BST is %d ",
optimalSearchTree(keys, freq, n));
return 0;
}
|
Java
public class Optimal_BST2 {
static int optimalSearchTree(int keys[], int freq[], int n) {
int cost[][] = new int[n + 1][n + 1];
for (int i = 0; i < n; i++)
cost[i][i] = freq[i];
for (int L = 2; L <= n; L++) {
for (int i = 0; i <= n - L + 1; i++) {
int j = i + L - 1;
cost[i][j] = Integer.MAX_VALUE;
int off_set_sum = sum(freq, i, j);
for (int r = i; r <= j; r++) {
int c = ((r > i) ? cost[i][r - 1] : 0)
+ ((r < j) ? cost[r + 1][j] : 0) + off_set_sum;
if (c < cost[i][j])
cost[i][j] = c;
}
}
}
return cost[0][n - 1];
}
static int sum(int freq[], int i, int j) {
int s = 0;
for (int k = i; k <= j; k++) {
if (k >= freq.length)
continue;
s += freq[k];
}
return s;
}
public static void main(String[] args) {
int keys[] = { 10, 12, 20 };
int freq[] = { 34, 8, 50 };
int n = keys.length;
System.out.println("Cost of Optimal BST is "
+ optimalSearchTree(keys, freq, n));
}
}
|
Python3
INT_MAX = 2147483647
def optimalSearchTree(keys, freq, n):
cost = [[0 for x in range(n)]
for y in range(n)]
for i in range(n):
cost[i][i] = freq[i]
for L in range(2, n + 1):
for i in range(n - L + 2):
j = i + L - 1
off_set_sum = sum(freq, i, j)
if i >= n or j >= n:
break
cost[i][j] = INT_MAX
for r in range(i, j + 1):
c = 0
if (r > i):
c += cost[i][r - 1]
if (r < j):
c += cost[r + 1][j]
c += off_set_sum
if (c < cost[i][j]):
cost[i][j] = c
return cost[0][n - 1]
def sum(freq, i, j):
s = 0
for k in range(i, j + 1):
s += freq[k]
return s
if __name__ == '__main__':
keys = [10, 12, 20]
freq = [34, 8, 50]
n = len(keys)
print("Cost of Optimal BST is",
optimalSearchTree(keys, freq, n))
|
C#
using System;
class GFG
{
static int optimalSearchTree(int []keys, int []freq, int n) {
int [,]cost = new int[n + 1,n + 1];
for (int i = 0; i < n; i++)
cost[i,i] = freq[i];
for (int L = 2; L <= n; L++) {
for (int i = 0; i <= n - L + 1; i++) {
int j = i + L - 1;
int off_set_sum = sum(freq, i, j);
cost[i,j] = int.MaxValue;
for (int r = i; r <= j; r++) {
int c = ((r > i) ? cost[i,r - 1] : 0)
+ ((r < j) ? cost[r + 1,j] : 0) + off_set_sum;
if (c < cost[i,j])
cost[i,j] = c;
}
}
}
return cost[0,n - 1];
}
static int sum(int []freq, int i, int j) {
int s = 0;
for (int k = i; k <= j; k++) {
if (k >= freq.Length)
continue;
s += freq[k];
}
return s;
}
public static void Main() {
int []keys = { 10, 12, 20 };
int []freq = { 34, 8, 50 };
int n = keys.Length;
Console.Write("Cost of Optimal BST is "
+ optimalSearchTree(keys, freq, n));
}
}
|
Javascript
<script>
function optimalSearchTree(keys, freq, n)
{
var cost = new Array(n);
for (var i = 0; i < n; i++)
cost[i] = new Array(n);
for (var i = 0; i < n; i++)
cost[i][i] = freq[i];
for (var L = 2; L <= n; L++)
{
for (var i = 0; i <= n-L+1; i++)
{
var j = i+L-1;
var off_set_sum = sum(freq, i, j);
if ( i >= n || j >= n)
break
cost[i][j] = Number. MAX_SAFE_INTEGER;
for (var r = i; r <= j; r++)
{
var c = 0;
if (r > i)
c += cost[i][r-1]
if (r < j)
c += cost[r+1][j]
c += off_set_sum;
if (c < cost[i][j])
cost[i][j] = c;
}
}
}
return cost[0][n-1];
}
function sum(freq, i, j)
{
var s = 0;
for (var k = i; k <= j; k++)
s += freq[k];
return s;
}
var keys = [10, 12, 20];
var freq = [34, 8, 50];
var n = keys.length;
document.write("Cost of Optimal BST is " +
optimalSearchTree(keys, freq, n));
</script>
|
OutputCost of Optimal BST is 142
Notes
1) The time complexity of the above solution is O(n^3). We have optimized the implementation by calculating the sum of the subarray freq[i…j] only once.
2) In the above solutions, we have computed optimal cost only. The solutions can be easily modified to store the structure of BSTs also. We can create another auxiliary array of size n to store the structure of the tree. All we need to do is, store the chosen ‘r’ in the innermost loop.
Recursive Memoized Solution
We can use the recursive solution with a dynamic programming approach to have a more optimized code, reducing the complexity from O(n^3) from the pure dynamic programming to O(n). To do that, we have to store the subproblems calculations in a matrix of NxN and use that in the recursions, avoiding calculating all over again for every recursive call.
C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 1000
int cost[MAX][MAX];
int Sum(int freq[], int i, int j) {
int s = 0;
for (int k = i; k <= j; k++)
s += freq[k];
return s;
}
int optCost_memoized(int freq[], int i, int j) {
if (cost[i][j])
return cost[i][j];
int fsum = Sum(freq, i, j);
int Min = INT_MAX;
for (int r = i; r <= j; r++) {
int c = optCost_memoized(freq, i, r - 1) + optCost_memoized(freq, r + 1, j) + fsum;
if (c < Min) {
Min = c;
cost[i][j] = c;
}
}
return cost[i][j];
}
int optimalSearchTree(int keys[], int freq[], int n) {
return optCost_memoized(freq, 0, n - 1);
}
int main() {
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = sizeof(keys) / sizeof(keys[0]);
memset(cost, 0, sizeof(cost));
for (int i = 0; i < n; i++)
cost[i][i] = freq[i];
cout << "Cost of Optimal BST is " << optimalSearchTree(keys, freq, n) << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
static final int MAX = 1000;
static int cost[][] = new int[MAX][MAX];
static int Sum(int freq[], int i, int j)
{
int s = 0;
for (int k = i; k <= j; k++)
s += freq[k];
return s;
}
static int optCost_memoized(int freq[], int i, int j)
{
if (i < 0 || j < 0)
return 0;
if (cost[i][j] != 0)
return cost[i][j];
int fsum = Sum(freq, i, j);
int Min = Integer.MAX_VALUE;
for (int r = i; r <= j; r++) {
int c = optCost_memoized(freq, i, r - 1)
+ optCost_memoized(freq, r + 1, j)
+ fsum;
if (c < Min) {
Min = c;
cost[i][j] = c;
}
}
return cost[i][j];
}
static int optimalSearchTree(int keys[], int freq[],
int n)
{
return optCost_memoized(freq, 0, n - 1);
}
public static void main(String[] args)
{
int keys[] = { 10, 12, 20 };
int freq[] = { 34, 8, 50 };
int n = keys.length;
for (int i = 0; i < n; i++)
Arrays.fill(cost[i], 0);
for (int i = 0; i < n; i++)
cost[i][i] = freq[i];
System.out.println(
"Cost of Optimal BST is "
+ optimalSearchTree(keys, freq, n));
}
}
|
Python3
def optCost_memoized(freq, i, j):
if cost[i][j]:
return cost[i][j]
fsum = Sum(freq, i, j)
Min = 999999999999
for r in range(i, j + 1):
c = (optCost_memoized(freq, i, r - 1) + optCost_memoized(freq, r + 1, j))
c += fsum
if c < Min:
Min = c
cost[i][j] = c
return cost[i][j]
def optimalSearchTree(keys, freq, n):
return optCost_memoized(freq, 0, n - 1)
def Sum(freq, i, j):
s = 0
for k in range(i, j + 1):
s += freq[k]
return s
if __name__ == '__main__':
keys = [10, 12, 20]
freq = [34, 8, 50]
n = len(keys)
cost = [[0 for x in range(n+1)] for y in range(n+1)]
for i in range(n):
cost[i][i] = freq[i]
print("Cost of Optimal BST is", optimalSearchTree(keys, freq, n))
|
C#
using System;
public class GFG {
const int MAX = 1000;
static int[, ] cost = new int[MAX, MAX];
static int Sum(int[] freq, int i, int j)
{
int s = 0;
for (int k = i; k <= j; k++)
s += freq[k];
return s;
}
static int optCost_memoized(int[] freq, int i, int j)
{
if (i < 0 || j < 0)
return 0;
if (cost[i, j] != 0)
return cost[i, j];
int fsum = Sum(freq, i, j);
int Min = int.MaxValue;
for (int r = i; r <= j; r++) {
int c = optCost_memoized(freq, i, r - 1)
+ optCost_memoized(freq, r + 1, j)
+ fsum;
if (c < Min) {
Min = c;
cost[i, j] = c;
}
}
return cost[i, j];
}
static int optimalSearchTree(int[] keys, int[] freq,
int n)
{
return optCost_memoized(freq, 0, n - 1);
}
public static void Main()
{
int[] keys = { 10, 12, 20 };
int[] freq = { 34, 8, 50 };
int n = keys.Length;
for (int i = 0; i < MAX; i++) {
for (int j = 0; j < MAX; j++) {
cost[i, j] = 0;
}
}
for (int i = 0; i < n; i++)
cost[i, i] = freq[i];
Console.WriteLine(
"Cost of Optimal BST is "
+ optimalSearchTree(keys, freq, n));
}
}
|
Javascript
const MAX = 1000;
let cost = new Array(MAX).fill(null).map(
() => new Array(MAX).fill(0));
function Sum(freq, i, j)
{
let s = 0;
for (let k = i; k <= j; k++)
s += freq[k];
return s;
}
function optCost_memoized(freq, i, j)
{
if (i < 0 || j < 0)
return 0;
if (cost[i][j])
return cost[i][j];
let fsum = Sum(freq, i, j);
let Min = Infinity;
for (let r = i; r <= j; r++) {
let c = optCost_memoized(freq, i, r - 1)
+ optCost_memoized(freq, r + 1, j) + fsum;
if (c < Min) {
Min = c;
cost[i][j] = c;
}
}
return cost[i][j];
}
function optimalSearchTree(keys, freq, n)
{
return optCost_memoized(freq, 0, n - 1);
}
let keys = [ 10, 12, 20 ];
let freq = [ 34, 8, 50 ];
let n = keys.length;
cost = new Array(MAX).fill(null).map(
() => new Array(MAX).fill(0));
for (let i = 0; i < n; i++)
cost[i][i] = freq[i];
console.log("Cost of Optimal BST is "
+ optimalSearchTree(keys, freq, n));
|
OutputCost of Optimal BST is 142
The time complexity of the above solution is O(n^3)
Share your thoughts in the comments
Please Login to comment...