Durbin Watson Test
Last Updated :
09 Mar, 2021
Durbin Watson Test: A test developed by statisticians professor James Durbin and Geoffrey Stuart Watson is used to detect autocorrelation in residuals from the Regression analysis. It is popularly known as Durbin-Watson d statistic, which is defined as
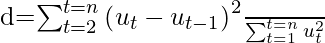
Let us first look at some terms to have a clear understanding-
- Regression Analysis — Regression analysis is a set of statistical methods used for the estimation of relationships between a dependent variable( Y ) and one or more independent variables( x ). This method helps determine which factors influence the results the most and should definitely be involved in the experiment, and those which can be ignored.
- Residuals — It is the difference between the calculated/observed value and the predicted value for a particular observation. Here the residuals are represented by u.
- Autocorrelation — Autocorrelation represents the degree of similarity between a given time series and a lagged version of itself over successive time intervals. Autocorrelation measures the relationship between a variable’s current value and its past values. For example — The air temperature values are calculated for all days of a month, and it is observed that the value on the 1st day is more similar to the value on the 2nd day than the value on the 30th day. So the data is said to be autocorrelated as the values which were observed closer in time are more similar than the values which were observed farther apart.
Assumptions of Durbin-Watson d Test
- The errors are normally distributed with a mean value of 0.
- The errors are stationary.
Null and Alternate Hypothesis of Durbin-Watson d Test
- Null Hypothesis: First order autocorrelation does not exist.
- Alternate Hypothesis: First order autocorrelation exists.
The above hypothesis is formulated to check for autocorrelation which can either be positive or negative. We can also check for the presence of positive autocorrelation and negative autocorrelation. The hypothesis will be formulated accordingly.
Test Statistic for Durbin-Watson d Test
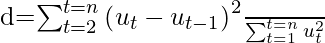
ut = the residual value for the tth observation.
u = Yactual - Ycalculated
number of observations in the experiment.
d = the ratio of the sum of squared differences in successive
residuals to the Residual
Sum of Squares(RSS).
Analyzing the Durbin-Watson d Statistic
The value of d always lies between 0 and 4. If d is close to 2 it means there is no autocorrelation, and we accept the null hypothesis. We find out the critical values dL and dU for the given data. dL is the Lower critical value and dU is the Upper critical value. Using these values the presence of autocorrelation is checked according to the decision rules mentioned below –
Testing for positive autocorrelation -
d < dL = positive autocorrelation is present
d > dU = No positive autocorrelation
dL < d < dU = Test is inconclusive
Testing for positive autocorrelation -
4-d < dL = negative autocorrelation is present
4-d > dU = No negative autocorrelation
dL < 4-d < dU = Test is inconclusive
On the basis of these rules, we either accept or reject the null hypothesis.
Steps to Perform Durbin-Watson d Test
Let us take an example to understand how to perform this test.
Example: Using the import and GNP data of U.K. test the autocorrelation of the data by applying Durbin-Watson d-statistic. Use 5% level of significance.
| Imports (Y) | 2.6 | 4.1 | 3.5 | 4.3 | 4.5 | 4.2 | 4.1 | 4.5 | 4.9 | 5.2 | 5.4 | 5.3 | 5.2 | 6.2 | 6.4 |
|---|
| GNP (X) | 21 | 22 | 22 | 23 | 24 | 24 | 25 | 25 | 25 | 26 | 28 | 29 | 29 | 30 | 32 |
|---|
Step 1: Run the regression analysis and obtain the residuals.
The regression line is given by –
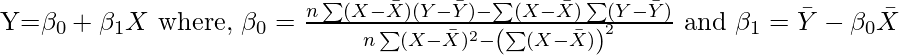
n = total number of observations.
Ā = mean value of A. Here A can be X or Y.
After calculating the equation for the regression line gets the corresponding Ycalculated values by putting the corresponding X values. Then get the values for residuals –
Residual(u) = Yactual - Ycalculated for each observation
Step 2: Compute the value of d.
Now put the required values and find the value of d.
For the given example the value for d will be 1.89.
Step 3: Find out the critical values dL and dU.
For the given sample size(n=15) and the number of independent variables k(in the given example it is 1) use the significance table to find the values.
The value of dL is 1.077 and dU is 1.361.
Step 4: Follow the decision rules mentioned above to conclude the results.
The rules which hold true are –
d > dU - No positive autocorrelation
4-d = 2.1 > dU - No negative autocorrelation.
Step 5: Conclude the results
Since there is no autocorrelation either positive or negative we accept the null hypothesis..
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...