Duplicates Removal in Array using BST
Last Updated :
13 Aug, 2021
Given an array arr[] of integers, the task is to remove duplicates from the given array.
Examples:
Input: arr[] = {1, 2, 3, 2, 5, 4, 4}
Output: arr[] = {1, 2, 3, 4, 5}
Input: arr[] = {127, 234, 127, 654, 355, 789, 355, 355, 999, 654}
Output: arr[] = {127, 234, 355, 654, 789, 999}
The duplicates in the array can be removed using Binary Search Tree. The idea is to create a Binary Search Tree using the array elements with the condition that the first element is taken as the root(parent) element and when the element “less” than root appears, it is made the left child and the element “greater” than root is made the right child of the root. Since no condition for “equal” exists the duplicates are automatically removed when we form a binary search tree from the array elements.
For the array, arr[] = {1, 2, 3, 2, 5, 4, 4}
BST will be:

Approach:
- Form BST using the array elements
- Display the elements using any Tree Traversal method.
Below is the implementation of the above approach.
C++
#include <iostream>
using namespace std;
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int data)
{
struct Node* nn
= new Node;
nn->data = data;
nn->left = NULL;
nn->right = NULL;
return nn;
}
struct Node* insert(struct Node* root, int data)
{
if (root == NULL)
return newNode(data);
else {
if (data < root->data)
root->left = insert(root->left, data);
if (data > root->data)
root->right = insert(root->right, data);
return root;
}
}
void inOrder(struct Node* root)
{
if (root == NULL)
return;
else {
inOrder(root->left);
cout << root->data << " ";
inOrder(root->right);
}
}
int main()
{
int arr[] = { 1, 2, 3, 2, 5, 4, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
struct Node* root = NULL;
for (int i = 0; i < n; i++) {
root = insert(root, arr[i]);
}
inOrder(root);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int data)
{
struct Node* nn
= (struct Node*)(malloc(sizeof(struct Node)));
nn->data = data;
nn->left = NULL;
nn->right = NULL;
return nn;
}
struct Node* insert(struct Node* root, int data)
{
if (root == NULL)
return newNode(data);
else {
if (data < root->data)
root->left = insert(root->left, data);
if (data > root->data)
root->right = insert(root->right, data);
return root;
}
}
void inOrder(struct Node* root)
{
if (root == NULL)
return;
else {
inOrder(root->left);
printf("%d ", root->data);
inOrder(root->right);
}
}
int main()
{
int arr[] = { 1, 2, 3, 2, 5, 4, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
struct Node* root = NULL;
for (int i = 0; i < n; i++) {
root = insert(root, arr[i]);
}
inOrder(root);
return 0;
}
|
Java
import java.util.Scanner;
class Node
{
int data;
public Node left;
public Node right;
Node(int data)
{
this.data = data;
left = right = null;
}
}
class GFG
{
public static Node insert(Node root, int data)
{
if (root == null)
return new Node(data);
if (data < root.data)
root.left = insert(root.left, data);
if (data > root.data)
root.right = insert(root.right, data);
return root;
}
public static void inOrder(Node root)
{
if (root == null)
return;
inOrder(root.left);
System.out.print(root.data+" ");
inOrder(root.right);
}
public static void main(String []args){
int arr[] = { 1, 2, 3, 2, 5, 4, 4 };
int n = arr.length;
Node root = null;
for (int i = 0; i < n; i++)
{
root = insert(root,arr[i]);
}
inOrder(root);
}
}
|
Python3
class newNode :
def __init__(self,data) :
self.data = data;
self.left = None;
self.right = None;
def insert(root, data) :
if (root == None) :
return newNode(data);
else :
if (data < root.data) :
root.left = insert(root.left, data);
if (data > root.data) :
root.right = insert(root.right, data);
return root;
def inOrder(root) :
if (root == None) :
return;
else :
inOrder(root.left);
print(root.data, end = " ");
inOrder(root.right);
if __name__ == "__main__" :
arr = [ 1, 2, 3, 2, 5, 4, 4 ];
n = len(arr);
root = None;
for i in range(n) :
root = insert(root, arr[i]);
inOrder(root);
|
C#
using System;
public class Node
{
public int data;
public Node left;
public Node right;
public Node(int data)
{
this.data = data;
left = right = null;
}
}
class GFG{
public static Node insert(Node root, int data)
{
if (root == null)
return new Node(data);
if (data < root.data)
root.left = insert(root.left, data);
if (data > root.data)
root.right = insert(root.right, data);
return root;
}
public static void inOrder(Node root)
{
if (root == null)
return;
inOrder(root.left);
Console.Write(root.data + " ");
inOrder(root.right);
}
static void Main()
{
int[] arr = { 1, 2, 3, 2, 5, 4, 4 };
int n = arr.Length;
Node root = null;
for(int i = 0; i < n; i++)
{
root = insert(root, arr[i]);
}
inOrder(root);
}
}
|
Javascript
<script>
class Node
{
constructor(data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
function insert(root, data)
{
if (root == null)
return new Node(data);
if (data < root.data)
root.left = insert(root.left, data);
if (data > root.data)
root.right = insert(root.right, data);
return root;
}
function inOrder(root)
{
if (root == null)
return;
inOrder(root.left);
document.write(root.data + " ");
inOrder(root.right);
}
var arr = [1, 2, 3, 2, 5, 4, 4 ];
var n = arr.length;
var root = null;
for(var i = 0; i < n; i++)
{
root = insert(root, arr[i]);
}
inOrder(root);
</script>
|
Time Complexity: 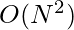 in the worst case(when the array is sorted) where N is the size of the given array.
in the worst case(when the array is sorted) where N is the size of the given array.
Auxiliary Space: O(N).
Share your thoughts in the comments
Please Login to comment...