Open In App

Draw circle using polar equation and Bresenham’s equation

Last Updated : 23 Mar, 2024
Improve
Improve
Like Article
Like
Save
Share
Report

In this article, we will discuss how to draw circles using Bresenham Equation and Polar Equation.

Circle Drawing Algorithm

It is not easy to display a continuous smooth arc on the computer screen as our computer screen is made of pixels organized in matrix form. So, to draw a circle on a computer screen it should always choose the nearest pixels from a printed pixel so as they could form an arc.

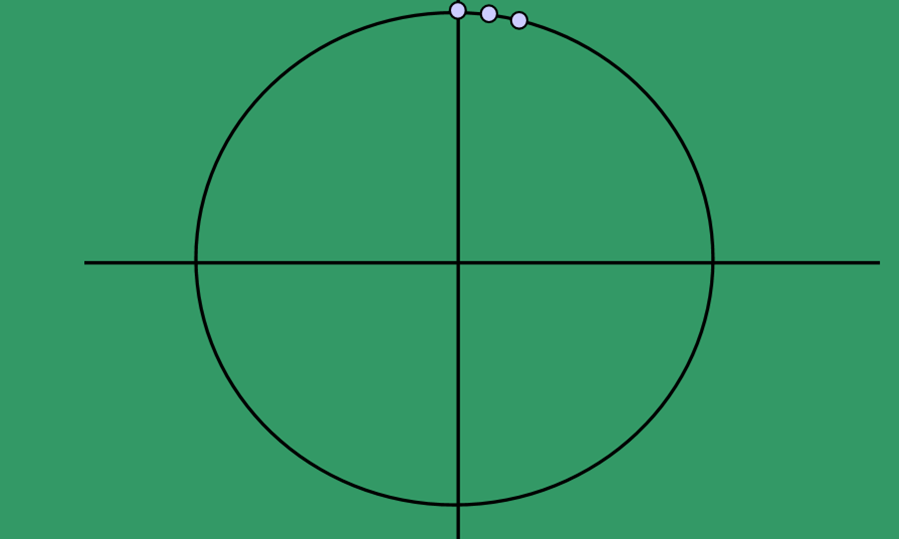
  • Consider circles centered at the origin with integer radii.
  • Can apply translations to get non-origin centered circles.

  • Equation of circle is given by:

x2 + y2 =  R2
y = +/-sqrt(R2-x2)

  • The given equation can be written as:

F(x, y)= x2+ y2-R2=0
5.

  • Use of Symmetry: Only need to calculate one octant. One can get points in the other 7 octants as follows:
    • Plotpoint(x, y)
    • Plotpoint(y, x)
    • Plotpoint(x, -y)
    • Plotpoint(-y, x)
    • Plotpoint(-x, -y)
    • Plotpoint(-y, -x)
    • Plotpoint(-x, y)
    • Plotpoint(-y, x)

Circle Drawing Using Bresenham Equation

Bresenham Equation uses the key feature of a circle that is highly symmetric. So, for the whole 360 degrees circle, divide it into 8-parts each octant of 45 degrees. In order to that, the idea is to use Bresenham’s Circle Algorithm for the calculation of the locations of the pixels in the first octant of 45 degrees. It assumes that the circle is centered on the origin. So for every pixel (x, y) draw a pixel in each of the 8 octants of the circle as shown below:

In Bresenham’s Algorithm at any point (x, y) we have two options either to choose the next pixel in the east i.e., (x + 1, y) or in the south-east i.e., (x + 1, y – 1). And this can be decided by using the decision parameter d as:

  • If d > 0, then (x + 1, y – 1) is to be chosen as the next pixel as it will be closer to the arc.
  • Else (x + 1, y) is to be chosen as the next pixel.

Below is the algorithm for Bresenham Equation:

  • F(x, y) = x2 + y2 = 0 Point lies on the circle.
  • F(x, y) > 0 Point lies outside the circle.
  • F(x, y) < 0 Point lies inside the circle.
  • If d >= 0 then update x as (x + 1) and y = (y – 1) which gives new d
  • If d < 0 then update x as (x + 1) which gives the new value of d
C++ 
#include <GL/glut.h>
#include <iostream>

float xo = 0, yo = 0, r = 0;

void drawCircle() {
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1, 0, 0);
    glPointSize(2);

    float x = 0;
    float y = r;
    float p = 5 / 4.0f - r;

    glBegin(GL_POINTS);

    while (y > x) {
        if (p < 0) {
            x += 1;
            p = p + 2 * x + 1;
        } else {
            y -= 1;
            x += 1;
            p = p + 2 * (x - y) + 1;
        }

        glVertex2f(x + xo, y + yo);
        glVertex2f(-x + xo, y + yo);
        glVertex2f(x + xo, -y + yo);
        glVertex2f(-x + xo, -y + yo);
        glVertex2f(y + yo, x + xo);
        glVertex2f(-y + yo, x + xo);
        glVertex2f(y + yo, -x + xo);
        glVertex2f(-y + yo, -x + xo);
    }

    glEnd();
    glFlush();
}

void init() {
    glClearColor(1, 1, 1, 1);
    glOrtho(-500, 500, -500, 500, -1, 1);
}

int main(int argc, char** argv) {
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
    glutInitWindowSize(1000, 1000);
    glutInitWindowPosition(100, 100);
    glutCreateWindow("GeeksforGeeks");

    std::cout << "Enter X, Y, and radius in the console." << std::endl;
    std::cout << "Enter X-coordinate: ";
    std::cin >> xo;
    std::cout << "Enter Y-coordinate: ";
    std::cin >> yo;
    std::cout << "Enter radius: ";
    std::cin >> r;

    init();
    glutDisplayFunc(drawCircle);
    glutMainLoop();

    return 0;
}
//This code is contributed by Utkarsh
C 
// C program for the above approach
#include <GL/gl.h>
#include <GL/glut.h>
#include <math.h>
#include <stdio.h>

int xo, yo, r;

// Function to display the circle using
// the above algorithm
void Display(void)
{
    glClear(GL_COLOR_BUFFER_BIT);

    // Color of printing object
    glColor3f(1, 0, 0);

    // Giving the size of the point
    glPointSize(2);

    int x = 0;
    int y = r;
    float p = 5 / 4 - r;

    glColor3f(1, 0, 0);

    // Starting of drawing the circle
    glBegin(GL_POINTS);

    while (y > x) {
        if (p < 0) {

            // Increment x to x+1
            x++;
            p = p + 2 * x + 1;
        }
        else {

            // Increment x to x+1
            // and decrease y to y-1
            y--;
            x++;
            p = p + 2 * (x - y) + 1;
        }

        // Draw the coordinates
        glVertex2d(x + xo, y + yo);
        glVertex2d(-x + xo, y + yo);
        glVertex2d(x + xo, -y + yo);
        glVertex2d(-x + xo, -y + yo);
        glVertex2d(y + yo, x + xo);
        glVertex2d(-y + yo, x + xo);
        glVertex2d(y + yo, -x + xo);
        glVertex2d(-y + yo, -x + xo);
    }

    glEnd();

    // Its empties all the buffer
    // causing the issue
    glFlush();
}

// Driver Code
int main(int argc, char** argv)
{
    printf("X-coordinate Y-coordinate radius:");
    scanf("%d %d %d", &xo, &yo, &r);
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);

    // Assigning the size of window
    glutInitWindowSize(1000, 1000);

    // Assign the position of window
    // to be appeared
    glutInitWindowPosition(100, 100);

    // Defining the heading of the window
    glutCreateWindow("GeeksforGeeks");

    // Backgronnd Color
    glClearColor(1, 1, 1, 1);

    // limit of the coordinate points
    gluOrtho2D(-500, 500, -500, 500);

    // Calling the function
    glutDisplayFunc(Display);

    glutMainLoop();

    return 0;
}
Java 
import javax.swing.*;
import javax.media.opengl.*;
import java.awt.*;

public class CircleDrawing extends JFrame implements GLEventListener {

    private static final long serialVersionUID = 1L;
    private float xo = 0, yo = 0, r = 0;

    public static void main(String[] args) {
        SwingUtilities.invokeLater(() -> {
            new CircleDrawing().setVisible(true);
        });
    }

    public CircleDrawing() {
        setTitle("GeeksforGeeks");
        setSize(1000, 1000);
        setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);

        GLCanvas canvas = new GLCanvas();
        canvas.addGLEventListener(this);

        add(canvas);
        setVisible(true);

        JOptionPane.showMessageDialog(this, "Enter X, Y, and radius in the console.");
        xo = Float.parseFloat(JOptionPane.showInputDialog("Enter X-coordinate:"));
        yo = Float.parseFloat(JOptionPane.showInputDialog("Enter Y-coordinate:"));
        r = Float.parseFloat(JOptionPane.showInputDialog("Enter radius:"));
    }

    @Override
    public void init(GLAutoDrawable drawable) {
        GL gl = drawable.getGL();
        gl.glClearColor(1, 1, 1, 1);
        gl.glOrtho(-500, 500, -500, 500, -1, 1);
    }

    @Override
    public void display(GLAutoDrawable drawable) {
        GL gl = drawable.getGL();
        GLU glu = new GLU();

        gl.glClear(GL.GL_COLOR_BUFFER_BIT);

        // Color of printing object
        gl.glColor3f(1, 0, 0);

        // Giving the size of the point
        gl.glPointSize(2);

        float x = 0;
        float y = r;
        float p = 5 / 4.0f - r;

        // Starting of drawing the circle
        gl.glBegin(GL.GL_POINTS);

        while (y > x) {
            if (p < 0) {
                // Increment x to x+1
                x += 1;
                p = p + 2 * x + 1;
            } else {
                // Increment x to x+1 and decrease y to y-1
                y -= 1;
                x += 1;
                p = p + 2 * (x - y) + 1;
            }

            // Draw the coordinates
            gl.glVertex2d(x + xo, y + yo);
            gl.glVertex2d(-x + xo, y + yo);
            gl.glVertex2d(x + xo, -y + yo);
            gl.glVertex2d(-x + xo, -y + yo);
            gl.glVertex2d(y + yo, x + xo);
            gl.glVertex2d(-y + yo, x + xo);
            gl.glVertex2d(y + yo, -x + xo);
            gl.glVertex2d(-y + yo, -x + xo);
        }

        gl.glEnd();

        // Flush all the buffer causing the issue
        gl.glFlush();
    }

    @Override
    public void reshape(GLAutoDrawable drawable, int x, int y, int width, int height) {
       
    }

    @Override
    public void dispose(GLAutoDrawable drawable) {
       
    }

    // This Code is Contributed by Shivam Tiwari
}
Python 
from OpenGL.GL import *
from OpenGL.GLUT import *
import math

xo, yo, r = 0, 0, 0

# Function to display the circle using the above algorithm
def Display():
    glClear(GL_COLOR_BUFFER_BIT)

    # Color of printing object
    glColor3f(1, 0, 0)

    # Giving the size of the point
    glPointSize(2)

    x = 0
    y = r
    p = 5 / 4.0 - r  # Corrected the division to use floating-point arithmetic

    glColor3f(1, 0, 0)

    # Starting of drawing the circle
    glBegin(GL_POINTS)

    while y > x:
        if p < 0:
            # Increment x to x+1
            x += 1
            p = p + 2 * x + 1
        else:
            # Increment x to x+1 and decrease y to y-1
            y -= 1
            x += 1
            p = p + 2 * (x - y) + 1

        # Draw the coordinates
        glVertex2d(x + xo, y + yo)
        glVertex2d(-x + xo, y + yo)
        glVertex2d(x + xo, -y + yo)
        glVertex2d(-x + xo, -y + yo)
        glVertex2d(y + yo, x + xo)
        glVertex2d(-y + yo, x + xo)
        glVertex2d(y + yo, -x + xo)
        glVertex2d(-y + yo, -x + xo)

    glEnd()

    # Flush all the buffer causing the issue
    glFlush()

# Driver Code
def main():
    global xo, yo, r
    xo, yo, r = map(int, input("X-coordinate Y-coordinate radius:").split())

    glutInit()
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)

    # Assigning the size of window
    glutInitWindowSize(1000, 1000)

    # Assign the position of window to be appeared
    glutInitWindowPosition(100, 100)

    # Defining the heading of the window
    glutCreateWindow(b"GeeksforGeeks")

    # Background Color
    glClearColor(1, 1, 1, 1)

    # Limit of the coordinate points
    gluOrtho2D(-500, 500, -500, 500)

    # Calling the function
    glutDisplayFunc(Display)

    glutMainLoop()

if __name__ == "__main__":
    main()
C# 
using System;
using OpenTK;
using OpenTK.Graphics;
using OpenTK.Graphics.OpenGL;
using OpenTK.Input;

namespace CircleDrawing
{
    class Program : GameWindow
    {
        // Center coordinates (X, Y) and radius (r) for the circle
        float xo = 0, yo = 0, r = 0;

        // Constructor to initialize the OpenTK window
        public Program(int width, int height) : base(width, height, GraphicsMode.Default, "GeeksforGeeks")
        {
            // Prompt user to input circle parameters
            Console.WriteLine("Enter X, Y, and radius in the console.");
            Console.Write("Enter X-coordinate: ");
            xo = float.Parse(Console.ReadLine());
            Console.Write("Enter Y-coordinate: ");
            yo = float.Parse(Console.ReadLine());
            Console.Write("Enter radius: ");
            r = float.Parse(Console.ReadLine());

            // Set vertical synchronization for smoother rendering
            VSync = VSyncMode.On;
        }

        // Method to draw the circle using the midpoint circle drawing algorithm
        void DrawCircle()
        {
            // Clear the color buffer
            GL.Clear(ClearBufferMask.ColorBufferBit);
            // Set the drawing color to red
            GL.Color3(1.0f, 0.0f, 0.0f);
            // Set the point size to 2 pixels
            GL.PointSize(2.0f);

            // Initialize circle drawing variables
            float x = 0;
            float y = r;
            float p = 5 / 4.0f - r;

            // Begin drawing points
            GL.Begin(PrimitiveType.Points);

            // Loop to draw the circle points
            while (y > x)
            {
                if (p < 0)
                {
                    x += 1;
                    p = p + 2 * x + 1;
                }
                else
                {
                    y -= 1;
                    x += 1;
                    p = p + 2 * (x - y) + 1;
                }

                // Draw points in all octants
                GL.Vertex2(x + xo, y + yo);
                GL.Vertex2(-x + xo, y + yo);
                GL.Vertex2(x + xo, -y + yo);
                GL.Vertex2(-x + xo, -y + yo);
                GL.Vertex2(y + yo, x + xo);
                GL.Vertex2(-y + yo, x + xo);
                GL.Vertex2(y + yo, -x + xo);
                GL.Vertex2(-y + yo, -x + xo);
            }

            // End drawing points
            GL.End();
            // Swap the front and back buffers for double buffering
            SwapBuffers();
        }

        // Method to initialize OpenGL settings
        protected override void OnLoad(EventArgs e)
        {
            // Set the clear color to white
            GL.ClearColor(1.0f, 1.0f, 1.0f, 1.0f);
            // Set the orthographic projection matrix
            GL.Ortho(-500, 500, -500, 500, -1, 1);
        }

        // Method called on each frame to render the circle
        protected override void OnRenderFrame(FrameEventArgs e)
        {
            DrawCircle();
        }

        // Main method to create and run the program
        [STAThread]
        static void Main()
        {
            // Create an instance of the Program class with a window size of 1000x1000
            using (Program program = new Program(1000, 1000))
            {
                // Run the program with a target frame rate of 30 frames per second
                program.Run(30);
            }
        }
    }
}
Javascript 
let xo = 0, yo = 0, r = 0;

// Function to display the circle using the above algorithm
function Display() {
    glClear(GL_COLOR_BUFFER_BIT);

    // Color of printing object
    glColor3f(1, 0, 0);

    // Giving the size of the point
    glPointSize(2);

    let x = 0;
    let y = r;
    let p = 5 / 4.0 - r; // Corrected the division to use floating-point arithmetic

    glColor3f(1, 0, 0);

    // Starting of drawing the circle
    glBegin(GL_POINTS);

    while (y > x) {
        if (p < 0) {
            // Increment x to x+1
            x += 1;
            p = p + 2 * x + 1;
        } else {
            // Increment x to x+1 and decrease y to y-1
            y -= 1;
            x += 1;
            p = p + 2 * (x - y) + 1;
        }

        // Draw the coordinates
        glVertex2d(x + xo, y + yo);
        glVertex2d(-x + xo, y + yo);
        glVertex2d(x + xo, -y + yo);
        glVertex2d(-x + xo, -y + yo);
        glVertex2d(y + yo, x + xo);
        glVertex2d(-y + yo, x + xo);
        glVertex2d(y + yo, -x + xo);
        glVertex2d(-y + yo, -x + xo);
    }

    glEnd();

    // Flush all the buffer causing the issue
    glFlush();
}

// Driver Code
function main() {
    xo = prompt("Enter X-coordinate:");
    yo = prompt("Enter Y-coordinate:");
    r = prompt("Enter radius:");

    glutInit();
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);

    // Assigning the size of window
    glutInitWindowSize(1000, 1000);

    // Assign the position of window to be appeared
    glutInitWindowPosition(100, 100);

    // Defining the heading of the window
    glutCreateWindow("GeeksforGeeks");

    // Background Color
    glClearColor(1, 1, 1, 1);

    // Limit of the coordinate points
    gluOrtho2D(-500, 500, -500, 500);

    // Calling the function
    glutDisplayFunc(Display);

    glutMainLoop();
}

// This Code is Contributed by Shivam Tiwari

Output:

Time Complexity: O(N)
Auxiliary Space: O(1)

Circle Using Polar Equation

In the Polar Equation system, the idea is to think of a clock with one hand. Move out a distance r, sometimes called the modulus, along with the hand from the origin, then rotate the hand upward (counterclockwise) by an angle θ to reach the point. Below is the algorithm for the Polar Equation:

  1. Initialize the variables rad, center(x0, y0), index value or increment value i, and define a circle using polar coordinates θ_end = 100.
  2. If θ_end < θ, then exit from the loop.
  3. Find the value of x as rad*cos(angle) and y as rad*sin(angle).
  4. Plot the eight points, found by symmetry i.e., the center (x0, y0) at the current (x, y) coordinates.
    •  Plot (x + xo, y + yo)
    • Plot (-x + xo, -y + yo)
    • Plot (y + xo, x + yo)
    • Plot (-y + xo, -x + yo)
    • Plot (-y + xo, x + yo)
    • Plot (y + xo, -x + yo)
    • Plot (-x + xo, y + yo)
    • Plot (x + xo, -y + yo)
  5. Increment the angle by i*2*(M_PI/100).

Below is the program to implement the above approach:

C++ 
#include <iostream>
#include <SDL.h>
#include <OpenGL/gl.h>
#include <OpenGL/glu.h>
#include <cmath>

void display(float xo, float yo, float rad) {
    // Clear previous frame
    glClear(GL_COLOR_BUFFER_BIT);
    
    // Set drawing color to white
    glColor3f(1, 1, 1);

    float angle = 0;

    // Begin drawing a polygon
    glBegin(GL_POLYGON);

    // Loop through 100 points to form the circle
    for (int i = 0; i < 100; ++i) {
        angle = i * 2 * (M_PI / 100);
        
        // Calculate x and y coordinates based on the angle and radius
        glVertex2f(xo + (cos(angle) * rad),
                   yo + (sin(angle) * rad));
    }

    glEnd();

    // Update the display
    SDL_GL_SwapBuffers();
}

int main(int argc, char* argv[]) {
    // Initialize SDL
    if (SDL_Init(SDL_INIT_VIDEO) < 0) {
        std::cerr << "Failed to initialize SDL: " << SDL_GetError() << std::endl;
        return 1;
    }

    // Take input values for x, y coordinates, and radius
    float xo, yo, rad;
    std::cout << "Enter x y radius: ";
    std::cin >> xo >> yo >> rad;

    // Set OpenGL attributes
    SDL_GL_SetAttribute(SDL_GL_DOUBLEBUFFER, 1);
    SDL_GL_SetAttribute(SDL_GL_DEPTH_SIZE, 24);
    SDL_GL_SetAttribute(SDL_GL_RED_SIZE, 8);
    SDL_GL_SetAttribute(SDL_GL_GREEN_SIZE, 8);
    SDL_GL_SetAttribute(SDL_GL_BLUE_SIZE, 8);
    SDL_GL_SetAttribute(SDL_GL_ALPHA_SIZE, 8);

    // Create window
    SDL_Surface* screen = SDL_SetVideoMode(500, 500, 32, SDL_OPENGL);
    if (!screen) {
        std::cerr << "Failed to set video mode: " << SDL_GetError() << std::endl;
        SDL_Quit();
        return 1;
    }

    // Set the window title
    SDL_WM_SetCaption("GeeksforGeeks", nullptr);

    // Set background color to green
    glClearColor(0, 1, 0, 1);

    // Setting the coordinate limits for drawing
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluOrtho2D(-500, 500, -500, 500);
    glMatrixMode(GL_MODELVIEW);

    bool running = true;
    SDL_Event event;

    // Event loop to keep the window running and listen for events
    while (running) {
        while (SDL_PollEvent(&event)) {
            if (event.type == SDL_QUIT) {
                running = false;
            }
        }

        // Draw the circle in each frame
        display(xo, yo, rad);
    }

    // Close the SDL window
    SDL_Quit();

    return 0;
}
//Thi code is contributed by Prachi.
C 
// C program to demonstrate circle
// drawing using polar equation
#include <GL/glut.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
float xo, yo, rad;

// Function to display the circle
void display()
{
    glClear(GL_COLOR_BUFFER_BIT);

    // Color of printing object
    glColor3f(1, 1, 1);

    float angle;

    // Start to drawing the circle
    glBegin(GL_POLYGON);

    for (int i = 0; i < 100; i++) {

        // Change the angle
        angle = i * 2 * (M_PI / 100);
        glVertex2f(xo + (cos(angle) * rad),
                   yo + (sin(angle) * rad));
    }

    glEnd();

    // Its empties all the buffer
    // causing the issue
    glFlush();
}

// Driver Code
int main(int argc, char** argv)
{
    glutInit(&argc, argv);
    printf("Enter x y radius ");
    scanf("%f %f %f", &xo, &yo, &rad);

    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);

    // Assigning the size of window
    glutInitWindowSize(500, 500);

    // Assign the position of window
    // to be appeared
    glutInitWindowPosition(200, 200);

    // Defining the heading of the window
    glutCreateWindow("GeeksforGeeks");

    // Backgronnd Color
    glClearColor(0, 1, 0, 1);

    // limit of the coordinate points
    gluOrtho2D(-500, 500, -500, 500);

    // Calling the function
    glutDisplayFunc(Display);

    glutMainLoop();

    return 0;
}
Java 
import org.lwjgl.LWJGLException;
import org.lwjgl.opengl.Display;
import org.lwjgl.opengl.DisplayMode;
import org.lwjgl.opengl.GL11;
import org.lwjgl.util.glu.GLU;
import java.util.Scanner;

public class Main {
    // Function to display the circle
    public static void display(float xo, float yo, float rad) {
        // Clear the screen
        GL11.glClear(GL11.GL_COLOR_BUFFER_BIT);

        // Set drawing color to white
        GL11.glColor3f(1, 1, 1);

        float angle = 0;

        // Begin drawing a polygon
        GL11.glBegin(GL11.GL_POLYGON);

        // Loop through 100 points to form the circle
        for (int i = 0; i < 100; ++i) {
            angle = i * 2 * (float) Math.PI / 100;

            // Calculate x and y coordinates based on the angle and radius
            GL11.glVertex2f(xo + (float) Math.cos(angle) * rad,
                            yo + (float) Math.sin(angle) * rad);
        }

        GL11.glEnd();

        // Update the display
        Display.update();
    }

    public static void main(String[] args) {
        try {
            // Create the display
            Display.setDisplayMode(new DisplayMode(500, 500));
            Display.setTitle("GeeksforGeeks");
            Display.create();
        } catch (LWJGLException e) {
            e.printStackTrace();
            System.exit(1);
        }

        // Set background color to green
        GL11.glClearColor(0, 1, 0, 1);

        // Setting the coordinate limits for drawing
        GL11.glMatrixMode(GL11.GL_PROJECTION);
        GL11.glLoadIdentity();
        GLU.gluOrtho2D(-500, 500, -500, 500);
        GL11.glMatrixMode(GL11.GL_MODELVIEW);

        // Take input values for x, y coordinates, and radius
        Scanner scanner = new Scanner(System.in);
        System.out.print("Enter x y radius: ");
        float xo = scanner.nextFloat();
        float yo = scanner.nextFloat();
        float rad = scanner.nextFloat();

        // Event loop to keep the window running and listen for events
        while (!Display.isCloseRequested()) {
            // Draw the circle in each frame
            display(xo, yo, rad);
        }

        // Close the display
        Display.destroy();
    }
}
//This code is contributed by Monu.
C# 
using System;
using OpenTK;
using OpenTK.Graphics;
using OpenTK.Graphics.OpenGL;

class Program
{
    static void Display(float xo, float yo, float rad)
    {
        // Clear previous frame
        GL.Clear(ClearBufferMask.ColorBufferBit);

        // Set drawing color to white
        GL.Color3(1.0f, 1.0f, 1.0f);

        float angle = 0;

        // Begin drawing a polygon
        GL.Begin(PrimitiveType.Polygon);

        // Loop through 100 points to form the circle
        for (int i = 0; i < 100; ++i)
        {
            angle = i * 2 * (float)Math.PI / 100;

            // Calculate x and y coordinates based on the angle and radius
            GL.Vertex2(xo + (float)Math.Cos(angle) * rad,
                       yo + (float)Math.Sin(angle) * rad);
        }

        GL.End();

        // Update the display
        GL.Flush();
    }

    static void Main(string[] args)
    {
        using (var window = new GameWindow())
        {
            // Take input values for x, y coordinates, and radius
            float xo, yo, rad;
            Console.Write("Enter x y radius: ");
            string[] input = Console.ReadLine().Split();
            if (input.Length != 3 || !float.TryParse(input[0], out xo) || !float.TryParse(input[1], out yo) || !float.TryParse(input[2], out rad))
            {
                Console.WriteLine("Invalid input. Please enter three float values separated by spaces.");
                return;
            }

            // Set OpenGL version and attributes
            var glVersion = new GraphicsMode(new ColorFormat(32), 24, 8, 4);
            var glControl = new GraphicsContext(glVersion, window.WindowInfo);

            // Make the OpenGL context current
            glControl.MakeCurrent(window.WindowInfo);

            // Set background color to green
            GL.ClearColor(0.0f, 1.0f, 0.0f, 1.0f);

            window.Load += (sender, e) =>
            {
                // Drawing settings
                GL.MatrixMode(MatrixMode.Projection);
                GL.LoadIdentity();
                GL.Ortho(-500, 500, -500, 500, -1, 1);
                GL.MatrixMode(MatrixMode.Modelview);
            };

            window.Resize += (sender, e) =>
            {
                // Update viewport on window resize
                GL.Viewport(0, 0, window.Width, window.Height);
            };

            window.RenderFrame += (sender, e) =>
            {
                // Draw the circle in each frame
                Display(xo, yo, rad);
                window.SwapBuffers();
            };

            // Run the application loop
            window.Run();
        }
    }
}

//This code is contribiuuted by Utkarsh.
Javascript 
let xo, yo, rad;

function display() {
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Color of printing object
    gl.color3f(1, 1, 1);

    let angle;

    // Start drawing the circle
    gl.begin(gl.POLYGON);

    for (let i = 0; i < 100; i++) {
        // Change the angle
        angle = i * 2 * (Math.PI / 100);
        gl.vertex2f(xo + Math.cos(angle) * rad, yo + Math.sin(angle) * rad);
    }

    gl.end();

    // Flush the buffer
    gl.flush();
}

function main() {
    const canvas = document.createElement("canvas");
    document.body.appendChild(canvas);

    const gl = canvas.getContext("webgl");

    if (!gl) {
        console.log("Unable to initialize WebGL. Your browser may not support it.");
        return;
    }

    console.log("Enter x y radius (separated by spaces):");
    // You might want to replace this with a form of user input
    // For simplicity, you can hardcode values here.
    xo = 0;
    yo = 0;
    rad = 50;

    gl.clearColor(0, 1, 0, 1);
    gl.ortho(-500, 500, -500, 500, -1, 1);

    // Calling the function
    gl.displayFunc(display);

    // Event listener for closing the window
    window.addEventListener('beforeunload', () => {
        // Clean up resources if needed
        // gl.deleteProgram(program);
    });

    gl.mainLoop();

    // This Code is Contributed by Shivam Tiwari
}
Python3 
import pygame
from pygame.locals import *
from OpenGL.GL import *
from OpenGL.GLUT import *
import math

def display():
    # Clear previous frame
    glClear(GL_COLOR_BUFFER_BIT)
    
    # Set drawing color to white
    glColor3f(1, 1, 1)  

    angle = 0

    # Begin drawing a polygon
    glBegin(GL_POLYGON)

    # Loop through 100 points to form the circle
    for i in range(100):
        angle = i * 2 * (math.pi / 100)
        
        # Calculate x and y coordinates based on the angle and radius
        glVertex2f(xo + (math.cos(angle) * rad),
                   yo + (math.sin(angle) * rad))

    glEnd()

    # Update the display
    pygame.display.flip()

if __name__ == "__main__":
    # Initialize pygame
    pygame.init()

    # Take input values for x, y coordinates and radius
    xo, yo, rad = map(float, input("Enter x y radius: ").split())

    display_mode = pygame.OPENGL | pygame.DOUBLEBUF
    
    # Set up display mode and window size
    pygame.display.set_mode((500, 500), display_mode)
    
    # Set the window title
    pygame.display.set_caption("GeeksforGeeks")
    
    # Set background color to green
    glClearColor(0, 1, 0, 1)  
    
    # Setting the coordinate limits for drawing
    gluOrtho2D(-500, 500, -500, 500)  

    running = True
    
    # Event loop to keep the window running and listen for events
    while running:
        for event in pygame.event.get():
            # Check for window close event
            if event.type == pygame.QUIT:
                running = False
        
        # Draw the circle in each frame
        display()

    # Close the pygame window
    pygame.quit()

# This Code Is Contributed By Shubham Tiwari

Output:

Time Complexity: O(N)
Auxiliary Space: O(1)



Like Article
Suggest improvement
Previous
Length of the transverse common tangent between the two non intersecting circles
Next
Count all possible N-length vowel permutations that can be generated based on the given conditions
Share your thoughts in the comments

Similar Reads

Draw circles using the polar coordinates and mid-point circle drawing algorithm on the same console using openGL in C++
Neighbors of a point on a circle using Bresenham's algorithm
Bresenham’s circle drawing algorithm
Equation of circle when three points on the circle are given
Comparisons between DDA and Bresenham Line Drawing algorithm
Illustration for tracing all the 8 octaves in Bresenham's line algorithm
Bresenham’s Line Generation Algorithm
Draw circle in C graphics
Draw an Ellipse rotating over a Circle in C++ graphics
Draw a circle without floating point arithmetic

N
naman1404
Article Tags :
Practice Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox