Double Threaded Binary Search Tree

Double Threaded Binary Search Tree: is a binary search tree in which the nodes are not every left NULL pointer points to its inorder predecessor and the right NULL pointer points to the inorder successor.
The threads are also useful for fast accessing the ancestors of a node.

 Double Threaded Binary Search Tree is one of the most used types of Advanced data structures used in many real-time applications like places where there are recent insertion and traversal of all elements of the search tree. 

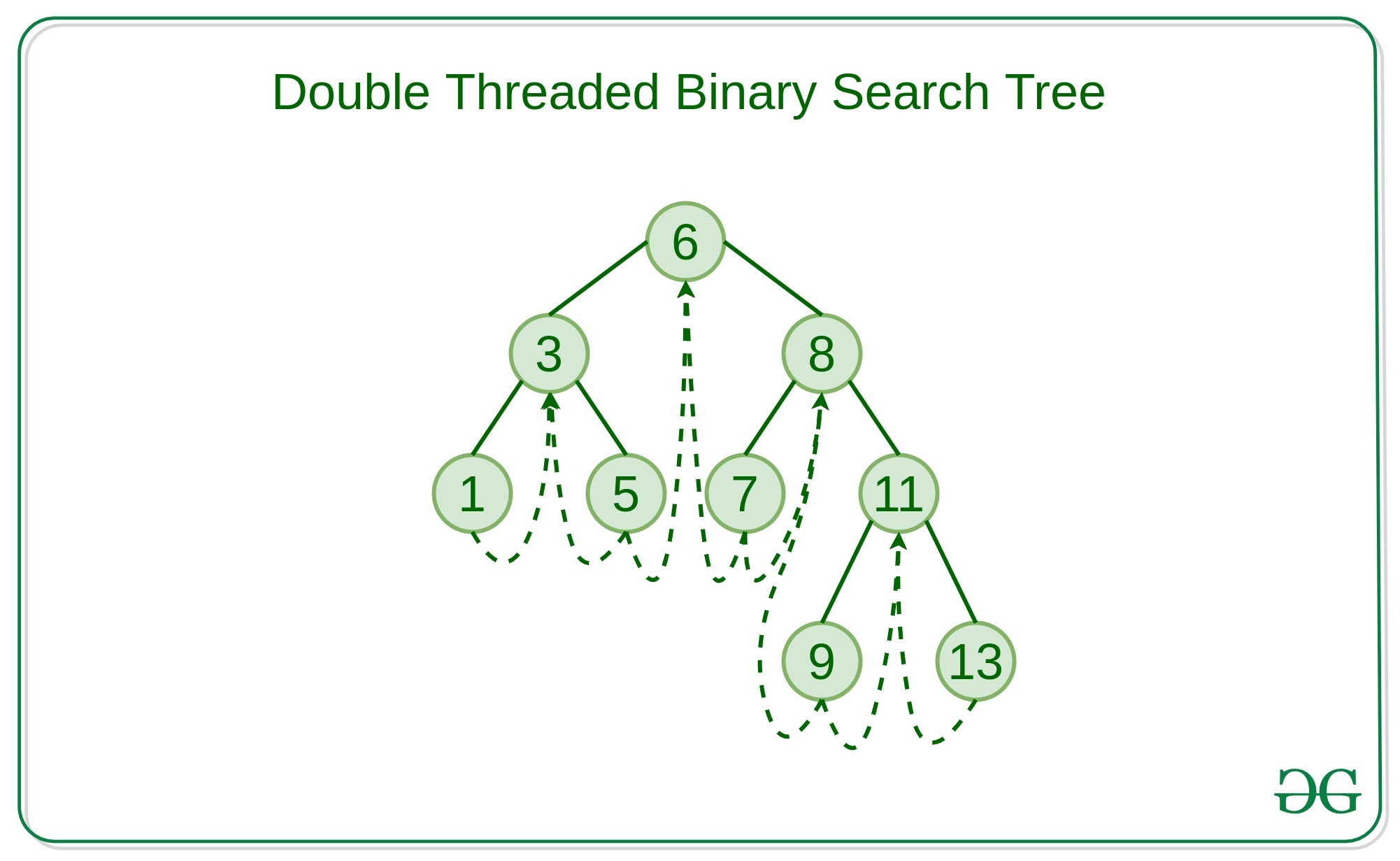
Creation algorithm for Double Threaded Binary Search Tree:

• In Double Threaded Binary search tree, there are five fields namely, data fields, left, right pointers, lbit, and rbit where lbit and rbit are boolean value stored to denote the right pointer points to an inorder successor or a new child node. Similarly, lbit denotes that the left pointer points to an inorder predecessor or a new child node.
• Base condition for the creation of the Double Threaded binary search tree is that the root node exists or not, If it doesn’t exist then create a new node and store it.
• Otherwise, compare the data of the current node to the new Data to be inserted, If the new data is less than the current data then traverse to the left child node. Otherwise, traverse to the right child node.
• If the left child or right child doesn’t exist then insert the node to its left and point its left and right child to the inorder predecessor and successor respectively.

Below is the implementation of the above approach: 

C++

// C++ implementation of the double
// threaded binary searighth tree

#include <iostream>
using namespace std;

// Class of the Node
class Node {
    int lbit, rbit;
    int value;
    Node *left, *right;

public:
    // Constructor of the
    // Node of the Tree
    Node()
    {
        lbit = rbit = 0;
        value = 0;
        left = right = NULL;
    }
    friend class DTBT;
};

// Class of the Threaded
// Binary search tree
class DTBT {
    Node* root;

public:
    // Constructor of the
    // Threaded of the Binary
    // Search Tree
    DTBT()
    {
        root = new Node();

        // Initialise the dummy node
        // to any random value of
        // your choice.
        root->value = 9999;

        // Considering our whole
        // tree is at left of
        // dummy node
        root->rbit = 1;
        root->lbit = 0;

        // Consider your whole tree
        // lies to the left of
        // this dummy node.
        root->left = root;
        root->right = root;
    }
    void create();
    void insert(int value);
    void preorder();
    Node* preorderSuccessor(Node*);
    void inorder();
    Node* inorderSuccessor(Node*);
};

// Function to create the Binary
// search tree
void DTBT::create()
{
    int n = 9;

    // Insertion of the nodes
    this->insert(6);
    this->insert(3);
    this->insert(1);
    this->insert(5);
    this->insert(8);
    this->insert(7);
    this->insert(11);
    this->insert(9);
    this->insert(13);
}

// Function to insert the nodes
// into the threaded binary
// search tree
void DTBT::insert(int data)
{
    // Condition to check if there
    // is no node in the binary tree
    if (root->left == root
        && root->right == root) {

        Node* p = new Node();
        p->value = data;
        p->left = root->left;
        p->lbit = root->lbit;
        p->rbit = 0;
        p->right = root->right;

        // Inserting the node in the
        // left of the dummy node
        root->left = p;
        root->lbit = 1;
        return;
    }

    // New node
    Node* cur = new Node;
    cur = root->left;
    while (1) {
        // Condition to check if the
        // data to be inserted is
        // less than the current node
        if (cur->value < data) {
            Node* p = new Node();
            p->value = data;
            if (cur->rbit == 0) {
                p->right = cur->right;
                p->rbit = cur->rbit;
                p->lbit = 0;
                p->left = cur;

                // Inserting the node
                // in the right
                cur->rbit = 1;
                cur->right = p;
                return;
            }
            else
                cur = cur->right;
        }

        // Otherwise insert the node
        // in the left of current node
        if (cur->value > data) {
            Node* p = new Node();
            p->value = data;
            if (cur->lbit == 0) {
                p->left = cur->left;
                p->lbit = cur->lbit;
                p->rbit = 0;

                // Pointing the right child
                // to its inorder Successor
                p->right = cur;
                cur->lbit = 1;
                cur->left = p;
                return;
            }
            else
                cur = cur->left;
        }
    }
}

// In Threaded binary search tree
// the left pointer of every node
// points to its Inorder predecessor,
// whereas its right pointer points
// to the Inorder Successor
void DTBT::preorder()
{
    Node* c = root->left;

    // Loop to traverse the tree in
    // the preorder fashion
    while (c != root) {
        cout << " " << c->value;
        c = preorderSuccessor(c);
    }
}

// Function to find the preorder
// Successor of the node
Node* DTBT::preorderSuccessor(Node* c)
{
    if (c->lbit == 1) {
        return c->left;
    }
    while (c->rbit == 0) {
        c = c->right;
    }
    return c->right;
}

// In Threaded binary search tree
// the left pointer of every node
// points to its Inorder predecessor
// whereas its right pointer points
// to the Inorder Successor
void DTBT::inorder()
{
    Node* c;
    c = root->left;
    while (c->lbit == 1)
        c = c->left;

    // Loop to traverse the tree
    while (c != root) {
        cout << " " << c->value;
        c = inorderSuccessor(c);
    }
}

// Function to find the inorder
// successor of the node
Node* DTBT::inorderSuccessor(Node* c)
{
    if (c->rbit == 0)
        return c->right;
    else
        c = c->right;
    while (c->lbit == 1) {
        c = c->left;
    }
    return c;
}

// Driver Code
int main()
{
    DTBT t1;

    // Creation of the Threaded
    // Binary search tree
    t1.create();

    cout << "Inorder Traversal of DTBST\n";
    t1.inorder();

    cout << "\nPreorder Traversal of DTBST\n";
    t1.preorder();
    return 0;
}

Python3

# Python implementation of the double
# threaded binary searighth tree

# Class of the Node
class Node:
    def __init__(self):
        self.lbit = None
        self.rbit = None
        self.value = None
        self.left = None
        self.right = None

# Class of the Threaded
# Binary search tree
class DTBT:
    root = None

    # Constructor of the
    # Threaded of the Binary
    # Search Tree
    def __init__(self):
        self.root = Node()

        # Initialise the dummy node
        # to any random value of
        # your choice.
        self.root.value = 9999

        # Considering our whole
        # tree is at left of
        # dummy node
        self.root.rbit = 1
        self.root.lbit = 0

        # Consider your whole tree
        # lies to the left of
        # this dummy node.
        self.root.left = self.root
        self.root.right = self.root

    def create(self):
        n = 9

        # Insertion of the nodes
        self.insert(6)
        self.insert(3)
        self.insert(1)
        self.insert(5)
        self.insert(8)
        self.insert(7)
        self.insert(11)
        self.insert(9)
        self.insert(13)

    # Function to insert the nodes
    # into the threaded binary
    # search tree
    def insert(self, data):

        # Condition to check if there
        # is no node in the binary tree
        if (self.root.left == self.root and
            self.root.right == self.root):

            # New node
            p = Node()
            p.value = data
            p.left = self.root.left
            p.lbit = self.root.lbit
            p.rbit = 0
            p.right = self.root.right

            # Inserting the node in the
            # left of the dummy node
            self.root.left = p
            self.root.lbit = 1
            return

        # New node
        cur = self.root.left
        while (1):
            # Condition to check if the
            # data to be inserted is
            # less than the current node
            if (cur.value < data):
                p = Node()
                p.value = data
                if (cur.rbit == 0):
                    p.right = cur.right
                    p.rbit = cur.rbit
                    p.lbit = 0
                    p.left = cur

                    # Inserting the node
                    # in the right
                    cur.rbit = 1
                    cur.right = p
                    return
                else:
                    cur = cur.right

            # Otherwise insert the node
            # in the left of current node
            if (cur.value > data):
                p = Node()
                p.value = data
                if (cur.lbit == 0):
                    p.left = cur.left
                    p.lbit = cur.lbit
                    p.rbit = 0

                    # Pointing the right child
                    # to its inorder Successor
                    p.right = cur
                    cur.lbit = 1
                    cur.left = p
                    return
                else:
                    cur = cur.left

    # In Threaded binary search tree
    # the left pointer of every node
    # points to its Inorder predecessor,
    # whereas its right pointer points
    # to the Inorder Successor
    def preorder(self):
        c = self.root.left

        # Loop to traverse the tree in
        # the preorder fashion
        while (c != self.root):
            print(c.value, end = ' ')
            c = self.preorderSuccessor(c)

    # Function to find the preorder
    # Successor of the node
    def preorderSuccessor(self, c):
        if (c.lbit == 1):
            return c.left
        while (c.rbit == 0):
            c = c.right
        return c.right

    # In Threaded binary search tree
    # the left pointer of every node
    # points to its Inorder predecessor
    # whereas its right pointer points
    # to the Inorder Successor
    def inorder(self):
        c = self.root.left
        while (c.lbit == 1):
            c = c.left

        # Loop to traverse the tree
        while (c != self.root):
            print(c.value, end = ' ')
            c = self.inorderSuccessor(c)

    # Function to find the inorder
    # successor of the node
    def inorderSuccessor(self, c):
        if (c.rbit == 0):
            return c.right
        else:
            c = c.right
        while (c.lbit == 1):
            c = c.left
        return c

# Driver Code
if __name__ == '__main__':
    t1 = DTBT()

    # Creation of the Threaded
    # Binary search tree
    t1.create()

    print("Inorder Traversal of DTBST")
    t1.inorder()

    print("\nPreorder Traversal of DTBST")
    t1.preorder()

Javascript

// JavaScript implementation of the double
// threaded binary search tree

// Class of the Node
class Node {
    constructor() {
        this.lbit = null;
        this.rbit = null;
        this.value = null;
        this.left = null;
        this.right = null;
    }
}

// Class of the Threaded
// Binary search tree
class DTBT {
    constructor() {
        this.root = new Node();

        // Initialise the dummy node
        // to any random value of
        // your choice.
        this.root.value = 9999;

        // Considering our whole
        // tree is at left of
        // dummy node
        this.root.rbit = 1;
        this.root.lbit = 0;

        // Consider your whole tree
        // lies to the left of
        // this dummy node.
        this.root.left = this.root;
        this.root.right = this.root;

    }

    create() {
        const n = 9;
        // Insertion of the nodes
        this.insert(6);
        this.insert(3);
        this.insert(1);
        this.insert(5);
        this.insert(8);
        this.insert(7);
        this.insert(11);
        this.insert(9);
        this.insert(13);
    }

    // Function to insert the nodes
    // into the threaded binary
    // search tree
    insert(data) {
        // Condition to check if there
        // is no node in the binary tree
        if (
            this.root.left === this.root &&
            this.root.right === this.root
        ) {
            // New node
            const p = new Node();
            p.value = data;
            p.left = this.root.left;
            p.lbit = this.root.lbit;
            p.rbit = 0;
            p.right = this.root.right;

            // Inserting the node in the
            // left of the dummy node
            this.root.left = p;
            this.root.lbit = 1;
            return;
        }

        // New node
        let cur = this.root.left;
        while (true) {
            // Condition to check if the
            // data to be inserted is
            // less than the current node
            if (cur.value < data) {
                const p = new Node();
                p.value = data;
                if (cur.rbit === 0) {
                    p.right = cur.right;
                    p.rbit = cur.rbit;
                    p.lbit = 0;
                    p.left = cur;

                    // Inserting the node
                    // in the right
                    cur.rbit = 1;
                    cur.right = p;
                    return;
                } else {
                    cur = cur.right;
                }
            }

            // Otherwise insert the node
            // in the left of current node
            if (cur.value > data) {
                const p = new Node();
                p.value = data;
                if (cur.lbit === 0) {
                    p.left = cur.left;
                    p.lbit = cur.lbit;
                    p.rbit = 0;

                    // Pointing the right child
                    // to its inorder Successor
                    p.right = cur;
                    cur.lbit = 1;
                    cur.left = p;
                    return;
                } else {
                    cur = cur.left;
                }
            }
        }


    }


    // In Threaded binary search tree
    // the left pointer of every node
    // points to its Inorder predecessor,
    // whereas its right pointer points
    // to the Inorder Successor
    preorder() {
        let c = this.root.left;

        // Loop to traverse the tree in
        // the preorder fashion
        while (c != this.root) {
            process.stdout.write(c.value + " ");
            c = this.preorderSuccessor(c);
        }
    }

    // Function to find the preorder
    // Successor of the node
    preorderSuccessor(c) {
        if (c.lbit == 1) {
            return c.left;
        }

        while (c.rbit == 0) {
            c = c.right;
        }

        return c.right;
    }

    // In Threaded binary search tree
    // the left pointer of every node
    // points to its Inorder predecessor
    // whereas its right pointer points
    // to the Inorder Successor
    inorder() {
        let c = this.root.left;

        while (c.lbit == 1) {
            c = c.left;
        }

        // Loop to traverse the tree
        while (c != this.root) {
            process.stdout.write(c.value + " ");
            c = this.inorderSuccessor(c);
        }
    }

    // Function to find the inorder
    // successor of the node
    inorderSuccessor(c) {
        if (c.rbit == 0) {
            return c.right;
        } else {
            c = c.right;
        }

        while (c.lbit == 1) {
            c = c.left;
        }

        return c;
    }
}

let t1 = new DTBT();

// Creation of the Threaded Binary search tree
t1.create();

console.log("Inorder Traversal of DTBST");
t1.inorder();

console.log("\nPreorder Traversal of DTBST");
t1.preorder();

// The code is contributed by Nidhi goel.

Output

Inorder Traversal of DTBST
 1 3 5 6 7 8 9 11 13
Preorder Traversal of DTBST
 6 3 1 5 8 7 11 9 13