Don’t Care (X) Conditions in K-Maps
Last Updated :
25 May, 2023
One of the very significant and useful concepts in simplifying the output expression using K-Map is the concept of “Don’t Care”. The “Don’t Care” conditions allow us to replace the empty cell of a K-Map to form a grouping of the variables which is larger than that of forming groups without don’t care. While forming groups of cells, we can consider a “Don’t Care” cell as 1 or 0 or we can also ignore that cell. Therefore, the “Don’t Care” condition can help us to form a larger group of cells.
A Don’t Care cell can be represented by a cross(X) or minus(-) or phi(Φ) in K-Maps representing an invalid combination. For example, in the Excess-3 code system, the states 0000, 0001, 0010, 1101, 1110, and 1111 are invalid or unspecified. These states are called don’t cares.
A standard SOP function having don’t cares can be converted into a POS expression by keeping don’t cares as they are, and writing the missing minterms of the SOP form as the maxterm of POS form. Similarly, a POS function having don’t cares can be converted to SOP form keeping the don’t cares as they are and writing the missing maxterms of the POS expression as the minterms of SOP expression.
Example-1:
Minimise the following function in SOP minimal form using K-Maps:
f = m(1, 5, 6, 11, 12, 13, 14) + d(4)
Explanation:
The SOP K-map for the given expression is:

Therefore, SOP minimal is,
f = BC' + BD' + A'C'D + AB'CD
Example-2:
Minimise the following function in POS minimal form using K-Maps:
F(A, B, C, D) = m(0, 1, 2, 3, 4, 5) + d(10, 11, 12, 13, 14, 15)
Explanation:
Writing the given expression in POS form:
F(A, B, C, D) = M(6, 7, 8, 9) + d(12, 13, 14, 15)
The POS K-map for the given expression is:

Therefore, POS minimal is,
F = (A'+ C)(B' + C')
Example-3:
Minimise the following function in SOP minimal form using K-Maps:
F(A, B, C, D) = m(1, 2, 6, 7, 8, 13, 14, 15) + d(0, 3, 5, 12)
Explanation:
The SOP K-map for the given expression is:
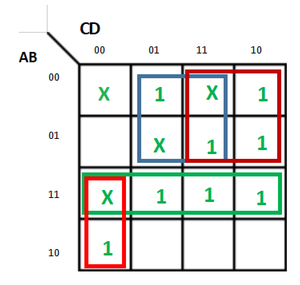
Therefore,
f = AC'D' + A'D + A'C + AB
Significance of “Don’t Care” Conditions:
Don’t Care conditions has the following significance in designing of the digital circuits:
- Simplification of the output:
These conditions denotes inputs that are invalid for a given digital circuit. Thus, they can used to further simplify the boolean output expression of a digital circuit.
- Reduction in number of gates required:
Simplification of the expression reduces the number of gates to be used for implementing the given expression. Therefore, don’t cares make the digital circuit design more economical.
- Reduced Power Consumption:
While grouping the terms along with don’t cares reduces switching of the states. This decreases the memory space that is required to represent a given digital circuit which in turn results in less power consumption.
- Represent Invalid States in Code Converters:
These are used in code converters. For example- In design of 4-bit BCD-to-XS-3 code converter, the input combinations 1010, 1011, 1100, 1101, 1110, and 1111 are don’t cares.
- Prevention of Hazards in Digital Circuits:
Don’t cares also prevents hazards in digital systems.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...