Do parallel lines meet at infinity?
Last Updated :
27 Sep, 2021
When we draw two parallel lines on paper, they never meet. If we draw two parallel lines on a very large canvas as big as a playground even then they do not seem to meet but is it the same case for when the lines are so long and far away from any point that we can see. The discussion of parallel lines meeting at infinity needs some maths and a bit of imagination behind it, in this article we will achieve but we must first understand what we mean by parallel lines. A few simple definitions given below can be used to identify a set of parallel lines.
What are Parallel Lines?
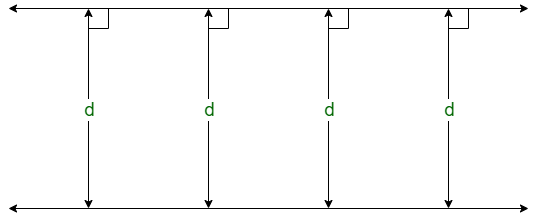
a) Two lines are said to be parallel if the perpendicular distance between them remains the same throughout, no matter how far the lines are extended.
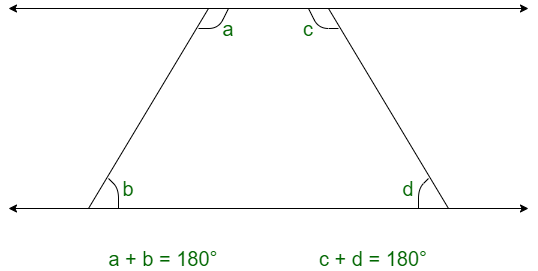
b) Two lines are said to be parallel if the sum of co-interior angles between them on the transversal is always 180°.
c) Two lines are said to be parallel if their slopes (gradient) are always equal.
What is Slope?
It is the tangent of the angle made by the line with the x-axis when the angle is measured anti-clockwise.
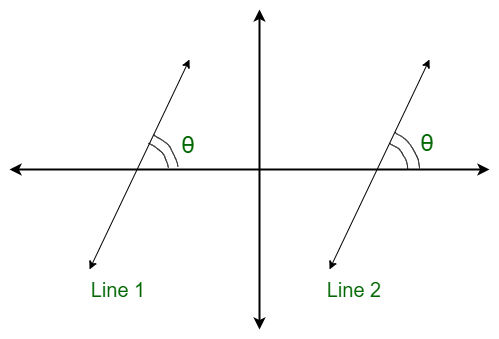
Slope = tanθ
Slope of line 1 = Slope of line 2
Now if we look at the three concepts we can observe the following:
- If the perpendicular distance is always constant, then the lines can never meet no matter how far the lines are extended.
- If the sum of co-interior angles is always 180°, then the lines can never meet otherwise the angle will be greater or less than 180°.
- If the slope has to be always equal, then the lines must never meet.
These three concepts are studied taking the lines on 2-dimensional coordinate planes. If we talk about 2-dimensional coordinate planes considering the above three concepts, then we can safely assume that the lines will never meet at infinity.
Assumptions and Observations
Let’s try to visualize the concept of parallelism and infinity in some more depth.

In the above diagram, let us assume that points A and B are at infinity and we are at point C. If we look at the two lines to our left and right, they appear parallel. Now when we move towards point A or B, no matter how far we go or how far we stand, the lines will always appear parallel to us because we will never be able to reach A or B because we can never reach infinity.
So even if we assume that the lines may intersect at infinity we can never know for sure.
Conceptually and diagrammatically we may meet these lines at infinity in 2-dimensional plane, but we will never know.
Someone can assume for a moment that all the lines in the world we can think of originating from a single point and that point is infinity. Or we can assume that every point originates infinite lines from it which travel infinitely.
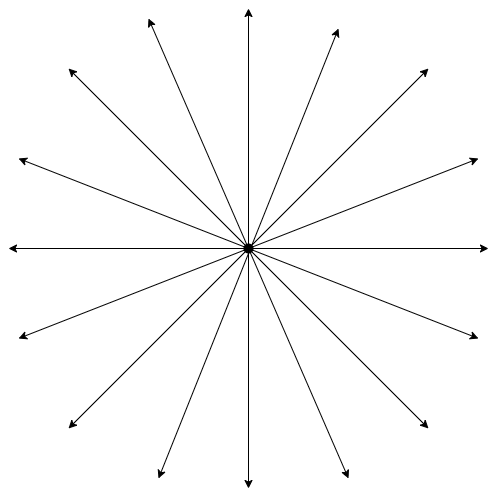
So according to the above assumption, if we see two or more than 2 parallel lines in front of us we can assume that they have originated from a single point at infinity from where all lines have been assumed to originate.
But again this is just an assumption made by someone because infinity is not a number we can think of in terms of distance or a place we can reach. So we can believe the above assumption but we can never prove for sure.
An interesting analogy is of railway tracks. Though they are parallel if we stand on it and look far beyond, they appear to meet. But this is just our perspective, a trick of the mind. If we try to reach that point where the tracks meet, we’ll see that the point moves further away from us and we can never reach it. Even though the tracks appear to meet at a point but there is no such point.
Conclusion
So the answer to the question, whether parallel lines meet at infinity? Well, the answer is yes as well as no depending on our perspective. We can say, yes, they meet at infinity or no, they never meet even at infinity, but we’ll never know for sure simply because we cannot comprehend infinity.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...