Dixon’s Factorization Method with implementation

Dixon’s Factorization method is an integer factorization algorithm. In this article, this method is explained to find the factors of a composite number. Dixon Factorization is based on the well-known fact of number theory that:

• If 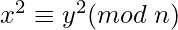with 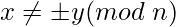it is likely that gcd(x – y, n) will be factor of n.

For example:

if N = 84923, by starting at 292, the first number greater than √N and counting up 5052 mod 84923 = 256 = 16² So (505 – 16)(505 + 16) = 0 mod 84923. Computing the greatest common divisor of 505 – 16 and N using Euclid’s algorithm gives 163, which is a factor of N.

Dixon’s Factorization Algorithm:

• Step 1: Choose a bound B and identify the factor base (P) of all primes less than or equal to B.
• Step 2: Search for positive integer z, such that 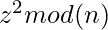is B-Smooth. 

  (1)

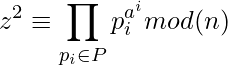
  B-Smooth: A positive integer is called B-Smooth if none of its prime factors is greater than B. For example:

720 has prime factorization as 2⁴ * 3² * 5¹ Therefore 720 is 5 smooth because none of its prime factors is greater than 5.

• Step 3: After generating enough of these relations (generally few more than the size of P), we use the method of linear algebra (e.g Gaussian Elimination) to multiply together these relations. Repeat this step until we formed a sufficient number of smooth squares.
• Step 4: After multiplying all these relations, we get the final equation say:

a2 = b2 mod(N)

• Step 5: Therefore, the factors of the above equation can be determined as:

GCD(a - b, N), GCD(a + b, N)

Step by Step execution of the Dixon’s Factorization Algorithm:

• Let’s say, we want to factor N = 23449 using bound B = 7. Therefore, the factor base P = {2, 3, 5, 7}.
• Here, x = ceil(sqrt(n)) = 154. So, we search randomly for integers between 154 and N whose squares are B-Smooth.
• As mentioned before, a positive integer is called B-Smooth if none of its prime factors is greater than B. So, let’s say, we find two numbers which are 970 and 8621 such that their none of their squares have prime factors greater than 7.
• Starting here the first related squares we get are:
  • 970² % 23499 = 2940 = 2² * 3 * 5 * 7²
  • 8621² % 23499 = 11760 = 2⁴ * 3 * 5 * 7²
• So, (970 * 8621)² = (2³ * 3 * 5 * 7²)² % 23499. That is: 14256² = 5880² % 23499.
• Now, we find:

gcd(14256 - 5880, 23449) = 131
gcd(14256 + 5880, 23449) = 179

• Therefore, the factors are: N = 131 * 179

Below is the implementation of the above approach: 

C++

// C++ implementation of Dixon factorization algo
#include<bits/stdc++.h>
using namespace std;
#include<vector>

// Function to find the factors of a number
// using the Dixon Factorization Algorithm
void factor(int n)
{

    // Factor base for the given number
    int base[4] = {2, 3, 5, 7};

    // Starting from the ceil of the root
    // of the given number N
    int start = int(sqrt(n));

    // Storing the related squares
    vector<vector<int> >pairs;

    // For every number from the square root
    // Till N
    int len=sizeof(base)/sizeof(base[0]);
    for(int i = start; i < n; i++)
    {
        vector<int> v;

        // Finding the related squares
        for(int j = 0; j < len; j++)
        {
            int lhs = ((int)pow(i,2))% n;
            int rhs = ((int)pow(base[j],2)) % n;

            // If the two numbers are the
            // related squares, then append
            // them to the array
            if(lhs == rhs)
            {
                v.push_back(i);
                v.push_back(base[j]);
                pairs.push_back(v);
            }

        }
    }

    vector<int>newvec;

    // For every pair in the array, compute the
    // GCD such that
    len = pairs.size();
    for (int i = 0; i < len;i++){
        int factor = __gcd(pairs[i][0] - pairs[i][1], n);

        // If we find a factor other than 1, then
        // appending it to the final factor array
        if(factor != 1)
            newvec.push_back(factor);

    }
    set<int>s;
    for (int i = 0; i < newvec.size(); i++)
        s.insert(newvec[i]);
    for(auto i = s.begin(); i != s.end(); i++)
        cout<<(*i)<<" ";
}

// Driver Code
int main()
{
    factor(23449);
}

// This code is contributed by chitranayal

Java

// Java implementation of Dixon factorization algo
import java.util.*;

class GFG {
    static int gcd(int num1, int num2)
    {
        int a = Math.abs(num1);
        int b = Math.abs(num2);
        while ((a != 0) && (b != 0) && (a != b)) {
            if (a > b) {
                a = a - b;
            }
            else {
                b = b - a;
            };
        };
        return a | b;
    }

    // Function to find the factors of a number
    // using the Dixon Factorization Algorithm
    static void factor(int n)
    {

        // Factor base for the given number
        int[] base1 = { 2, 3, 5, 7 };

        // Starting from the ceil of the root
        // of the given number N
        int start = (int)(Math.sqrt(n));

        // For every number from the square root
        // Till N
        int len = base1.length;

        // Storing the related squares
        ArrayList<ArrayList<Integer> > pairs
            = new ArrayList<ArrayList<Integer> >();

        for (int i = start; i < n; i++) {

            // Finding the related squares
            for (int j = 0; j < len; j++) {
                int lhs = ((int)Math.pow(i, 2)) % n;
                int rhs = ((int)Math.pow(base1[j], 2)) % n;

                // If the two numbers are the
                // related squares, then append
                // them to the array
                if (lhs == rhs) {
                    ArrayList<Integer> l1
                        = new ArrayList<Integer>();
                    l1.add(i);
                    l1.add(base1[j]);
                    pairs.add(l1);
                }
            }
        }

        ArrayList<Integer> newvec
            = new ArrayList<Integer>();

        // For every pair in the array, compute the
        // GCD such that
        len = pairs.size();
        for (int i = 0; i < len; i++) {
            int factor = gcd(pairs.get(i).get(0)
                                 - pairs.get(i).get(1),
                             n);

            // If we find a factor other than 1, then
            // appending it to the final factor array
            if (factor != 1)
                newvec.add(factor);
        }

        HashSet<Integer> s = new HashSet<Integer>();
        for (int i = 0; i < newvec.size(); i++)
            s.add(newvec.get(i));

        for (int s1 : s)
            System.out.print(s1 + " ");
    }

    // Driver Code
    public static void main(String[] args)
    {
        factor(23449);
    }
}

// This code is contributed by phasing17

Python3

# Python 3 implementation of Dixon factorization algo

from math import sqrt, gcd
import numpy as np

# Function to find the factors of a number
# using the Dixon Factorization Algorithm
def factor(n):

    # Factor base for the given number
    base = [2, 3, 5, 7]

    # Starting from the ceil of the root
    # of the given number N
    start = int(sqrt(n))

    # Storing the related squares
    pairs = []

    # For every number from the square root
    # Till N
    for i in range(start, n):

        # Finding the related squares
        for j in range(len(base)):
            lhs = i**2 % n
            rhs = base[j]**2 % n

            # If the two numbers are the
            # related squares, then append
            # them to the array
            if(lhs == rhs):
                pairs.append([i, base[j]])

    new = []

    # For every pair in the array, compute the
    # GCD such that
    for i in range(len(pairs)):
        factor = gcd(pairs[i][0] - pairs[i][1], n)

        # If we find a factor other than 1, then
        # appending it to the final factor array
        if(factor != 1):
            new.append(factor)

    x = np.array(new)

    # Returning the unique factors in the array
    return(np.unique(x))

# Driver Code
if __name__ == "__main__":
    print(factor(23449))

C#

// C# implementation of Dixon factorization algo
using System;
using System.Collections.Generic;

class GFG
{
  static int gcd (int num1, int num2) {
    int a = Math.Abs(num1);
    int b = Math.Abs(num2);
    while ( (a != 0) && (b != 0) && (a != b)) {
      if(a > b){
        a = a - b;
      }else{
        b = b - a;
      };
    };
    return a | b;
  }

  // Function to find the factors of a number
  // using the Dixon Factorization Algorithm
  static void factor(int n)
  {

    // Factor base for the given number
    int[] base1 = {2, 3, 5, 7};

    // Starting from the ceil of the root
    // of the given number N
    int start = (int)(Math.Sqrt(n));

    // Storing the related squares
    List<int []> pairs = new List<int []>();

    // For every number from the square root
    // Till N
    int len= base1.Length;
    for(int i = start; i < n; i++)
    {
      List<int> v = new List<int>();

      // Finding the related squares
      for(int j = 0; j < len; j++)
      {
        int lhs = ((int)Math.Pow(i, 2)) % n;
        int rhs = ((int)Math.Pow(base1[j], 2)) % n;

        // If the two numbers are the
        // related squares, then append
        // them to the array
        if(lhs == rhs)
        {
          pairs.Add(new [] {i, base1[j]});
        }

      }
    }

    List<int> newvec = new List<int>();

    // For every pair in the array, compute the
    // GCD such that
    len = pairs.Count;
    for (int i = 0; i < len;i++){
      int factor = gcd(pairs[i][0] - pairs[i][1], n);

      // If we find a factor other than 1, then
      // appending it to the final factor array
      if(factor != 1)
        newvec.Add(factor);

    }

    HashSet<int> s = new HashSet<int>();
    for (int i = 0; i < newvec.Count; i++)
      s.Add(newvec[i]);

    foreach (var s1 in s)
      Console.Write(s1 + " ");
  }

  // Driver Code
  public static void Main(string[] args)
  {
    factor(23449);
  }
}

// This code is contributed by phasing17

Javascript

// JS implementation of Dixon factorization algo
const gcd = (num1, num2) => {
   let a = Math.abs(num1);
   let b = Math.abs(num2);
   while (a && b && a !== b) {
      if(a > b){
         [a, b] = [a - b, b];
      }else{
         [a, b] = [a, b - a];
      };
   };
   return a || b;
};

// Function to find the factors of a number
// using the Dixon Factorization Algorithm
function factor(n)
{

    // Factor base for the given number
    let base = [2, 3, 5, 7];

    // Starting from the ceil of the root
    // of the given number N
    let start = Math.floor(Math.sqrt(n));

    // Storing the related squares
    let pairs = [];

    // For every number from the square root
    // Till N
    let len= base.length;
    for(let i = start; i < n; i++)
    {
        let v = [];

        // Finding the related squares
        for(let j = 0; j < len; j++)
        {
            let lhs = (i ** 2)% n;
            let rhs = ((base[j] ** 2)) % n;

            // If the two numbers are the
            // related squares, then append
            // them to the array
            if(lhs == rhs)
            {
                pairs.push([i, base[j]]);
            }

        }
    }

    let newvec = [];

    // For every pair in the array, compute the
    // GCD such that
    len = pairs.length;
    for (let i = 0; i < len;i++){
        let factor = gcd(pairs[i][0] - pairs[i][1], n);

        // If we find a factor other than 1, then
        // appending it to the final factor array
        if(factor != 1)
            newvec.push(factor);

    }

    let s = new Set();
    for (let i = 0; i < newvec.length; i++)
        s.add(newvec[i]);

    console.log(s)
}

// Driver Code
factor(23449);

// This code is contributed by phasing17

Output:

[131 179]

Time Complexity : O(sqrt(N))

Space complexity :  O(B)