Divisors of n-square that are not divisors of n

Given an positive large integer n. Count the number of positive divisors of n² which are not divisible by any divisor of n(1 <= n <= 10¹²). 

Input: 6
Output: 5
Explanation
Total divisors of 62 are 9 i.e.,
1, 2, 3, 4, 6, 9, 12, 18, 36
Total divisors of '6' are 4,
1, 2, 3, 6
Total divisor of '36' which are not
divisible by divisors of '6' are
'5' i.e., 4, 9, 12, 18, 36

Input: 8
Output: 3

Simple approach is to traverse for every divisor of n² and count only those divisors which are not divisor of ‘n’. Time complexity of this approach is O(n).
Efficient approach is to use prime factorization to count total divisors of n². A number ‘n’ can be represented as product of primes 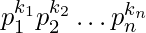. Refer this to understand more. 

Let 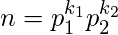 for some primes p1 and p2.Squaring both the sides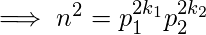Total factors of n2 will be,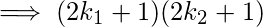Total factors of 'n' will be,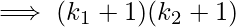Difference between the two gives the requiredanswer

C++

// C++ program to count number of
// divisors of n^2 which are not
// divisible by divisor of n
#include <bits/stdc++.h>
using namespace std;

// Function to count divisors of n^2
// having no factors of 'n'
int factors(long long n)
{
    unordered_map<int, int> prime;
    for (int i = 2; i <= sqrt(n); ++i) {
        while (n % i == 0) {

            // Increment count of i-th prime divisor
            ++prime[i];

            // Find next  prime divisor
            n = n / i;
        }
    }

    // Increment count if divisor still remains
    if (n > 2)
        ++prime[n];

    // Initialize variable for counting the factors
    // of  n^2 and n as ans1 and ans2 respectively
    int ans1 = 1, ans2 = 1;

    // Range based for-loop
    for (auto it : prime) {

        // Use formula as discussed in above
        ans1 *= 2 * it.second + 1;
        ans2 *= it.second + 1;
    }

    // return the difference of answers
    return ans1 - ans2;
}

// Driver code
int main()
{
    long long n = 5;
    cout << factors(n) << endl;
    n = 8;
    cout << factors(n);
    return 0;
}

Java

// Java program to count number of
// divisors of n^2 which are not
// divisible by divisor of n
import java.util.*;

class GFG
{

// Function to count divisors of n^2
// having no factors of 'n'
static int factors(int n)
{
    HashMap<Integer,
            Integer>prime = new HashMap<Integer,
                                        Integer>();
    for (int i = 2; i <= Math.sqrt(n); ++i)
    {
        while (n % i == 0)
        {

            // Increment count of i-th prime divisor
            if (prime.containsKey(i))
            {
                prime.put(i, prime.get(i) + 1);
            }

            else
            {
                prime.put(i, 1);
            }

            // Find next prime divisor
            n = n / i;
        }
    }

    // Increment count if divisor still remains
    if (n > 2)
    {
        if(prime.containsKey(n))
        {
            prime.put(n, prime.get(n) + 1);
        }
        else
        {
            prime.put(n, 1);
        }
    }

    // Initialize variable for counting the factors
    // of n^2 and n as ans1 and ans2 respectively
    int ans1 = 1, ans2 = 1;

    // Range based for-loop
    for (Map.Entry<Integer,
                   Integer> it : prime.entrySet())
    {

        // Use formula as discussed in above
        ans1 *= 2 * it.getValue() + 1;
        ans2 *= it.getValue() + 1;
    }

    // return the difference of answers
    return ans1 - ans2;
}

// Driver code
public static void main(String[] args)
{
    int n = 5;
    System.out.println(factors(n));
    n = 8;
    System.out.println(factors(n));
}
}

// This code is contributed by PrinciRaj1992

Python3

# Python3 program to count number of
# divisors of n^2 which are not
# divisible by divisor of n
import math as mt

# Function to count divisors of n^2
# having no factors of 'n'
def factors(n):

    prime = dict()
    for i in range(2, mt.ceil(mt.sqrt(n + 1))):
        while (n % i == 0):

            # Increment count of i-th
            # prime divisor
            if i in prime.keys():
                prime[i] += 1
            else:
                prime[i] = 1

            # Find next prime divisor
            n = n // i

    # Increment count if divisor
    # still remains
    if (n > 2):
        if n in prime.keys():
            prime[n] += 1
        else:
            prime[n] = 1

    # Initialize variable for counting
    # the factors of n^2 and n as ans1
    # and ans2 respectively
    ans1 = 1
    ans2 = 1

    # Range based for-loop
    for it in prime:

        # Use formula as discussed in above
        ans1 *= 2 * prime[it] + 1
        ans2 *= prime[it] + 1

    # return the difference of answers
    return ans1 - ans2

# Driver code
n = 5
print(factors(n))
n = 8
print(factors(n))

# This code is contributed by
# Mohit kumar 29

C#

// C# program to count number of
// divisors of n^2 which are not
// divisible by divisor of n
using System;
using System.Collections.Generic;

class GFG
{

// Function to count divisors of n^2
// having no factors of 'n'
static int factors(int n)
{
    Dictionary<int,
               int> prime = new Dictionary<int,
                                           int>();
    for (int i = 2; i <= Math.Sqrt(n); ++i)
    {
        while (n % i == 0)
        {

            // Increment count of i-th prime divisor
            if (prime.ContainsKey(i))
            {
                prime[i] = prime[i] + 1;
            }

            else
            {
                prime.Add(i, 1);
            }

            // Find next prime divisor
            n = n / i;
        }
    }

    // Increment count if divisor still remains
    if (n > 2)
    {
        if(prime.ContainsKey(n))
        {
            prime[n] = prime[n] + 1;
        }
        else
        {
            prime.Add(n, 1);
        }
    }

    // Initialize variable for counting the factors
    // of n^2 and n as ans1 and ans2 respectively
    int ans1 = 1, ans2 = 1;

    // Range based for-loop
    foreach(KeyValuePair<int, int> it in prime)
    {

        // Use formula as discussed in above
        ans1 *= 2 * it.Value + 1;
        ans2 *= it.Value + 1;
    }

    // return the difference of answers
    return ans1 - ans2;
}

// Driver code
public static void Main(String[] args)
{
    int n = 5;
    Console.WriteLine(factors(n));
    n = 8;
    Console.WriteLine(factors(n));
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>
// Javascript program to count number of
// divisors of n^2 which are not
// divisible by divisor of n

// Function to count divisors of n^2
// having no factors of 'n'
function factors(n)
{
    let prime = new Map();
    for (let i = 2; i <= Math.sqrt(n); ++i)
    {
        while (n % i == 0)
        {

            // Increment count of i-th prime divisor
            if (prime.has(i))
            {
                prime.set(i, prime.get(i) + 1);
            }

            else
            {
                prime.set(i, 1);
            }

            // Find next prime divisor
            n = Math.floor(n / i);
        }
    }

    // Increment count if divisor still remains
    if (n > 2)
    {
        if(prime.has(n))
        {
            prime.set(n, prime.get(n) + 1);
        }
        else
        {
            prime.set(n, 1);
        }
    }

    // Initialize variable for counting the factors
    // of n^2 and n as ans1 and ans2 respectively
    let ans1 = 1, ans2 = 1;

    // Range based for-loop
    for (let [key, value] of prime.entries())
    {

        // Use formula as discussed in above
        ans1 *= 2 * value + 1;
        ans2 *= value + 1;
    }

    // return the difference of answers
    return ans1 - ans2;
}

// Driver code
let n = 5;
document.write(factors(n)+"<br>");
n = 8;
document.write(factors(n)+"<br>");



// This code is contributed by unknown2108
</script>

Output:

1
3

Time complexity: O(log(n)) 
Auxiliary space: O(n) as using unordered_map