Division of Algebraic Expressions

An algebraic expression can be written as the product of its factors. Consider an expression, 7yz +3y. We see that 7yz can be written as 7 × y × z. The factors 7,y, and z can not be further expressed as product of factors. So, we can conclude that 7 × y × z is an irreducible form of 7yz.

Expressing the algebraic expression as a product of its factors is called factorization. Factors can be represented in form of numbers, variables or algebraic expressions. 

Techniques of Factorization 

Let us understand four ways of factorization   

Technique of Common Factors

In this method, each term is written as a product of irreducible factors. Then the common factors are identified and expressed using the distributive law.

Example: Factorize 18y²z +21 yz²

Solution:

18y²z = 2 × 3 × 3 × y × y × z

21yz² = 3 ×7 × y × z × z

Common factors : 3, y, z

So, 

18y²z +21 zy² = (2 × 3 × 3 × y × y × z) + (3 ×7 × y × z × z)

                       = 3 × y × z (6 × y + 7 × z)

                       = 3 y z(6y + 7z)

Technique of regrouping terms

Many times there is no common factor to all terms of the expression. In such a situation, the terms are regrouped until the factors reach the state of being irreducible.

Example: Factorize 16mn – 12m +12n – 9

Solution:

It is clear that in this expression, there are no common factors among all the terms. We need to regroup the terms.

16mn-12m = 4m(4n-3)

12n-9 = 3 (4n-3)

So, 16mn – 12m +12n -9 = 4m(4n-3)+3 (4n-3)

              We can take 4n-3 common between these terms

                        = (4n-3) (4m+3)

Technique of using Identities

We can make use of identities for factorization.

(a + b)² = a² + 2ab +b² ——–(I)

(a-b)² = a² + b² – 2ab ———-(II)

(a + b) (a- b)= a² -b² ———–(III)

Example 1: Factorize 25 x² – 49

Solution:

25 x² – 49 = (5x)² – (7)²

Using (III), we can rewrite it as

 = (5x+7)(5x-7)

Example 2. Factorize m² + 36 + 12m

Solution: 

m² + 36 + 12m

= m² + 2(6)(m)+6²

Using (I) it can be written as

= (m+6)²

Technique to use the form (x +a) (x +b) as x² + (a + b)x + ab

We know that x² + (a + b)x +ab = (x +a)(x+ b)

Example: Factorize m² +3m+2

Here, we need to find the factors such that their sum is 3 while their product is 2.

These are 2,1

So, m²+ 3m + 2 = m² + 2m + m +2

                       = m(m+2) + 1(m+2)

                       = (m+1)(m+2)

Division of Algebraic Expressions 

Division is the inverse of multiplication. Before discussing division, let us recapitulate some terms associated with polynomials. Depending on the number of terms in an expression, we decide if it is a monomial, binomial or a polynomial. 

Monomial contains one term while a binomial contains two terms. Generally speaking, a polynomial contains one or more than one terms with a non-zero coefficient.

Example of monomial: 4xy, 89z, 56pqr, -9

Example of binomial: 34x+45y, 9xz+5xy

Example of polynomial: w+ x +y +z, 3r+5t-8z-7p

Let us consider the following cases for division:

Division of monomial by a monomial

This is the simplest case where both the dividend and divisor are monomials.  These are factorized and the common factors are cancelled out.

Example 1: Divide 24y³ by 8y

Solution:

24y³ can be written as 2* 2 * 2 * 3* y * y * y 

8y can be written as 2*2*2*y.

So, we need to evaluate (2* 2 * 2 * 3* y * y * y)/(2*2*2*y)

Cancelling the common factors,  

We obtain the result as 3 y² .

Check: 3y² x 8y =24y³

Example 2. Divide 20mnz by 4 m

Solution:

Dividend = 4 * 5 * m * n * z

Divisor = 4 * m

Dividing we get, (4* 5* m*n*z)/(4 *m)= 5 n z

Check: 4m* 5nz = 20 mnz

Division of polynomial by a monomial

Example 1: Divide 32(m²np+ mn²p+mnp²) by 4mnp

Solution:

Dividend= 32(m²np+ mn²p+mnp²) = 4 * 8 *m n p (m +n+ p)

Divisor= 4mnp

On dividing, (4 * 8 *m n p (m +n+ p)/(4mnp)

= 8(m+ n +p)

Example 2: Divide 36pqr + 12r by 4r 

Solution:

Dividend =36pqr+ 12r =12 r(3pq+1)

Divisor= 4r

So, (36pqr+ 12r ) / 4r can be written as

= 12 r (3pq+1) /4r 

= 4r *3 *(3pq+1)/4r

Canceling the common terms,

We get, 3(3pq+1)

Division of polynomial by a polynomial

Sometimes there are some common factors between the dividend and divisor. The strategy here also is to cancel the common factors to obtain the quotient.

Example 1: (12m² + 24m)/(m+2)

12m²+24 m can be written as 12m(m+2)

So, (12m² + 24 m)/(m+2) =12m(m+2)/(m+2)= 12m

So the quotient is 12m

Check: 12m × (m+2)= 12m²+24m

We may apply the long division method also to compute the quotient and remainder. The terms of dividend are divided repeatedly by the first term of the divisor.

Example 2: Divide m⁴-m³+m² +5 by m+1

Solution:

This dividend can be rewritten as  

m³(m+1)-2m²(m+1)+3m(m+1)-3(m+1)+8

= m+1(m³-2m²+3m-3)+8

Division by m+1 gives

Quotient =(m³-2m²+3m-3)

Remainder=8

Example 3: Divide m⁴ – n⁴ by m² – n²

Solution:

By using the identity a² -b² = (a-b) (a + b)

We can write m⁴ – n⁴ as (m² – n²)(m² + n²)

So, cancelling the common terms in dividend and divisor, we get the quotient as m²+n²

Error 

Generally an error is a mistake or difference occurred in the calculated value because of the inaccuracy of the calculated number from its true value.

Points to remember to avoid errors:

• Coefficient 1 is usually not written. While adding like terms, do not forget to include it in sum.

e.g. The sum 4x and x+4 is (4x+x+4) i.e. 5x+4 not 4x+4 only.

• While substituting negative values, make use of brackets.

e.g. The product of 5 and (2x+3) i.e. 5(2x+3) is equal to 10x+15 not 10x+9 only.

• When an expression written in a bracket is multiplied by a constant outside the bracket, open the brackets carefully. Make sure that each term of expression has to be multiplied by the constant.

e.g. If it is given that x=-2 then 5x-2 can be written as, 5(-2)-2 which is equal to -12.

• When squaring any monomial, both the contact coefficient and the variable are squared.

e.g. The square of 2x i.e. (2x)² is equal to 4x².

• When squaring a binomial, always use the correct formulae.

e.g. The square of (2x+3) i.e. (2x+3)² is equal to 4x²+9+12x.

• When a polynomial is divided by a monomial then each term of the numerator of the polynomial is divided by the monomial present in the denominator.

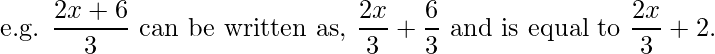
Conclusion:

This article teaches clearly various methods to do factorization. Also, it discusses the division of algebraic expression with proper examples.

• When a monomial is divided by other monomials, the coefficient of the quotient of two monomials is equal to the quotient of their coefficients.
• When a monomial is divided by other monomials, the variable of the quotient of two monomials is equal to the quotient of the variables of monomials.
• We can check the result by Dividend = Remainder + Divisor * Quotient