Division Algorithm for Polynomials

Polynomials are those algebraic expressions that contain variables, coefficients, and constants. For Instance, in the polynomial 8x² + 3z – 7, in this polynomial, 8,3 are the coefficients, x and z are the variables, and 7 is the constant. Just as simple Mathematical operations are applied on numbers, these operations can also be applied on different polynomials, applying different operations on polynomials gives a new polynomial, say p(x) is a polynomial multiplied with q(x), then, the new polynomial g(x) = p(x) × q(x).

Division Algorithm for Polynomials

Division algorithm states that, 

If p(x) and g(x) are two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that, 

p(x) = g(x) x g(x) + r(x) 

Where r(x) = 0 or degree of r(x) < degree of g(x) 

Dividend = Quotient × Divisor + Remainder 

Let’s look at some steps for doing this kind of division and then solve some examples related to it. 

1. In this step, arrange the divisor and dividend in an order which is decreasing according to their degrees.
2. First-term of the Quotient is given by dividing the highest degree term of the dividend by the highest degree term of the divisor. 
3. The second term of the quotient is obtained by dividing the highest degree term of the new dividend obtained as the remainder by the highest degree term of the divisor.
4. Continue this process till the degree of remainder is less than the degree of divisor.

Let’s look at some sample problems related to this algorithm.

Question 1: Divide the polynomial x³ + x² – 1 with x – 1. 

Solution: 

We just need to follow the same steps as mentioned above. 

So, the quotient here is x² + 2x + 2 and remainder is 1. 

Question 2: Divide the polynomial x⁴ + x³ + x² – 1 with x³ – 1. 

Solution:

So, the quotient comes out to be x + 1 and the remainder x² + x. 

Use of Division Algorithm in finding the zeros of a polynomial

Suppose we have a polynomial P(x) = 0 of degree 3. If we are given a root x = r of that polynomial. We can find the other two roots by dividing the polynomial with (x -r). Let’s see it with an example. 

Question 1: Find all the zeros of the polynomial f(x) = 2x³ -5x² -4x + 3 if one of roots is .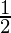 

Solution: 

x = 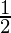 is a root of the polynomial (Given) 

Now we know from the fact stated above, (x – 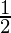) is a factor of the given polynomial. So, for finding out the other zeros, we need to divide the polynomial with this factor. 

So we get 2x² -4x – 6 as quotient. 

The remaining two roots are roots of this polynomial. 

2x² – 4x – 6 = 0

⇒ 2x² -6x + 2x – 6 = 0 

⇒ 2x(x – 3) + 2 (x – 3) = 0 

⇒ (2x + 2) (x – 3) = 0 

x = -1 and x = 3

Thus, the remaining two roots are x = -1 and x = 3. 

Question 2: Divide the polynomial 5x⁴ -3x³ + 2x² – 1 with x³ – 1. 

Solution:

The remainder is 3 and quotient is 5x³ + 2x² + 4x + 4

Question 3: Find all the zeros of 2x⁴ – 3x³ -3x² + 6x – 2. We know that two zeros are √2 and -√2. 

Solution: 

We are given two zeros of the polynomial. We know that, x – √2 and x + √2 are the factors of the polynomial. 

Two find the other roots let’s divide the polynomial with both of these. 

(x – √2)(x + √2) 

 = x² – 2

Dividing the polynomial with x² – 2. 

The quotient polynomial is given by 2x² – 3x + 1

The remaining two roots are also the roots of this polynomial. 

2x² – 3x + 1

⇒ 2x² – 2x -x + 1

⇒ 2x(x -1) -1(x – 1) 

⇒ (2x – 1) (x – 1) = 0

So, the roots come out to be x = and x= 1. 

Thus, all the roots are x = 1, √2, -√2 and 

My Personal Notes arrow_drop_up

Save