Dividing the rectangle into n right-angled triangles
Last Updated :
18 Jan, 2023
Puzzle: Find all values of n > 1 for which one can divide a rectangle into n right-angled triangles.
Answer:
We can divide any rectangle into n right-angled triangles, for any n > 1.
There are two methods to divide:
- Method 1:
- Case 1: n = 2, we can get two right-angled triangles by cutting the rectangle along the diagonal as shown in the figure.
For example: In the rectangle ABDC, we draw a diagonal BC and get two right-angled triangles, BDC and ABC.

- Case 2: n > 2, we first cut the rectangle along the diagonal and continue with n-2 cuts of any of the available right-angled triangles into two right-angled triangles, by cutting them along the height onto its hypotenuse.
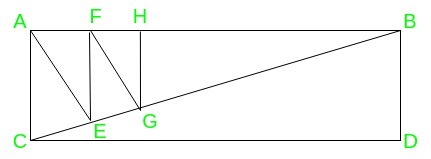
For example: Consider the case of n = 6, in the rectangle ABDC, we first draw diagonal BC, and then (n-2) i.e 4 cuts are made in the triangle ABC along with the height onto the hypotenuse, to get six right-angled triangles. These are BDC, ACE, AEF, FEG, FGH, HGB.
- Method 2: We can also solve the puzzle by considering it case-wise.
- Case 1: n is even: divide the rectangle into n/2 small rectangles and then can divide each of the smaller rectangle obtained, along its diagonal.
For example: For n=6, in the rectangle AGHB, we first form 3 smaller rectangles as ABCD, CEFD, EGHF. Then, we divide each rectangle along its hypotenuse BC, DE, FG respectively, to get 6 right-angled triangles

- Case 2: n is odd: In this case, first, divide the rectangle into n-1 small triangles using the approach mentioned above and then can cut any of the triangles along with the height onto its hypotenuse.
For example: For n=7, we first form 6 triangles as mentioned in the above point, and then we cut triangle ABC along with the height onto its hypotenuse, to obtain the 7th triangle AIB.

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...