Divide the array into minimum number of sub-arrays having unique elements
Last Updated :
30 Nov, 2022
Given an array arr. The task is to divide the array into the minimum number of subarrays containing unique elements and return the count of such subarrays.
Note: An array element cannot be present in more than one subarray.
Examples :
Input : arr[] = {1, 2, 1, 1, 2, 3}
Output : 3
Explanation : The subarrays having unique elements are { 1, 2 }, { 1 }, and { 1, 2, 3 }
Input : arr[] = {1, 2, 3, 4, 5}
Output : 1
Explanation : The subarray having unique elements is { 1, 2, 3, 4, 5 }
Approach:
The idea is to maintain a set while traversing the array. While traversing, if an element is already found in the set, then increase the count of subarray by 1 as we have to include the current element in the next subarray and clear the set for new subarray. Then, proceed for the complete array in a self-similar manner. The variable storing the count will be the answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumSubarrays(int ar[], int n)
{
set<int> se;
int cnt = 1;
for (int i = 0; i < n; i++) {
if (se.count(ar[i]) == 0) {
se.insert(ar[i]);
}
else {
cnt++;
se.clear();
se.insert(ar[i]);
}
}
return cnt;
}
int main()
{
int ar[] = { 1, 2, 1, 3, 4, 2, 4, 4, 4 };
int n = sizeof(ar) / sizeof(ar[0]);
cout << minimumSubarrays(ar, n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int minimumSubarrays(int ar[], int n)
{
Vector se = new Vector();
int cnt = 1;
for (int i = 0; i < n; i++)
{
if (se.contains(ar[i]) == false)
{
se.add(ar[i]);
}
else
{
cnt++;
se.clear();
se.add(ar[i]);
}
}
return cnt;
}
public static void main (String[] args)
{
int ar[] = { 1, 2, 1, 3, 4, 2, 4, 4, 4 };
int n = ar.length ;
System.out.println(minimumSubarrays(ar, n));
}
}
|
Python3
def minimumSubarrays(ar, n) :
se = []
cnt = 1;
for i in range(n) :
if se.count(ar[i]) == 0 :
se.append(ar[i])
else :
cnt += 1
se.clear()
se.append(ar[i])
return cnt
ar = [ 1, 2, 1, 3, 4, 2, 4, 4, 4 ]
n = len(ar)
print(minimumSubarrays(ar, n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int minimumSubarrays(int []ar, int n)
{
List<int> se = new List<int>();
int cnt = 1;
for (int i = 0; i < n; i++)
{
if (se.Contains(ar[i]) == false)
{
se.Add(ar[i]);
}
else
{
cnt++;
se.Clear();
se.Add(ar[i]);
}
}
return cnt;
}
public static void Main(String[] args)
{
int []ar = { 1, 2, 1, 3, 4, 2, 4, 4, 4 };
int n = ar.Length ;
Console.WriteLine(minimumSubarrays(ar, n));
}
}
|
Javascript
<script>
function minimumSubarrays(ar, n)
{
let se = new Set();
let cnt = 1;
for (let i = 0; i < n; i++)
{
if (se.has(ar[i]) == false)
{
se.add(ar[i]);
}
else
{
cnt++;
se.clear();
se.add(ar[i]);
}
}
return cnt;
}
let ar = [ 1, 2, 1, 3, 4, 2, 4, 4, 4 ];
let n = ar.length ;
document.write(minimumSubarrays(ar, n));
</script>
|
Time Complexity : 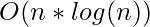
Auxiliary Space: O(n)
Method 2 Using Unordered_map
instead of using set we can use unordered_map for counting subarray without repeating elements in them. as above discussed if we use set in solution then it takes O(n*log(n)) time complexity rather than that if we use unordered_map in solution then time complexity will be O(n). so it’s better in terms of time complexity. below is the code for this solution
C++
#include <bits/stdc++.h>
using namespace std;
int minimumSubarrays(int ar[], int n)
{
unordered_map<int, int> mp;
int cnt = 1;
for (int i = 0; i < n; i++) {
if (mp[ar[i]]) {
cnt++;
mp.clear();
mp[ar[i]]++;
}
else {
mp[ar[i]]++;
}
}
return cnt;
}
int main() {
int ar[] = { 1, 2, 1, 3, 4, 2, 4, 4, 4 };
int n = sizeof(ar) / sizeof(ar[0]);
cout << minimumSubarrays(ar, n);
return 0;
}
|
Java
import java.util.*;
class GFG {
public static int minimumSubarrays(int ar[], int n)
{
Map < Integer, Integer > mp = new HashMap < Integer, Integer > ();
int cnt = 1;
for (int i = 0; i < n; i++) {
if (mp.containsKey(ar[i])) {
cnt++;
mp.clear();
mp.put(ar[i], 1);
} else {
mp.put(ar[i], 1);
}
}
return cnt;
}
public static void main(String[] args) {
int ar[] = {1, 2, 1, 3, 4, 2, 4, 4, 4 };
int n = ar.length;
System.out.println(minimumSubarrays(ar, n));
}
}
|
Python3
def minimumSubarrays(ar, n):
mp = {}
cnt = 1
for i in range(n):
if(ar[i] in mp):
cnt += 1
mp.clear()
mp[ar[i]] = 1
else:
mp[ar[i]] = 1
return cnt
ar = [1, 2, 1, 3, 4, 2, 4, 4, 4]
n = len(ar)
print(minimumSubarrays(ar, n))
|
C#
using System;
using System.Collections.Generic;
public class GFG {
public static int minimumSubarrays(int[] ar, int n) {
Dictionary < int, int > mp = new Dictionary < int, int > ();
int cnt = 1;
for (int i = 0; i < n; i++) {
if (mp.ContainsKey(ar[i])) {
cnt++;
mp.Clear();
mp[ar[i]] = 1;
} else {
mp[ar[i]] = 1;
}
}
return cnt;
}
public static void Main(string[] args) {
int[] ar = {1, 2, 1, 3, 4, 2, 4, 4, 4 };
int n = ar.Length;
Console.WriteLine(minimumSubarrays(ar, n));
}
}
|
Javascript
function minimumSubarrays(ar,n)
{
const mp = new Map();
let cnt = 1;
for (let i = 0; i < n; i++)
{
if (mp.has(ar[i]) == true)
{
cnt++;
mp.clear();
mp.set(ar[i],1);
}
else
{
mp.set(ar[i],1);
}
}
return cnt;
}
let ar = [1, 2, 1, 3, 4, 2, 4, 4, 4 ];
let n = ar.length;
console.log(minimumSubarrays(ar, n));
|
Time Complexity: O(n)
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...