Distance between Incenter and Circumcenter of a triangle using Inradius and Circumradius
Last Updated :
09 Sep, 2022
Given two integers r and R representing the length of Inradius and Circumradius respectively, the task is to calculate the distance d between Incenter and Circumcenter.
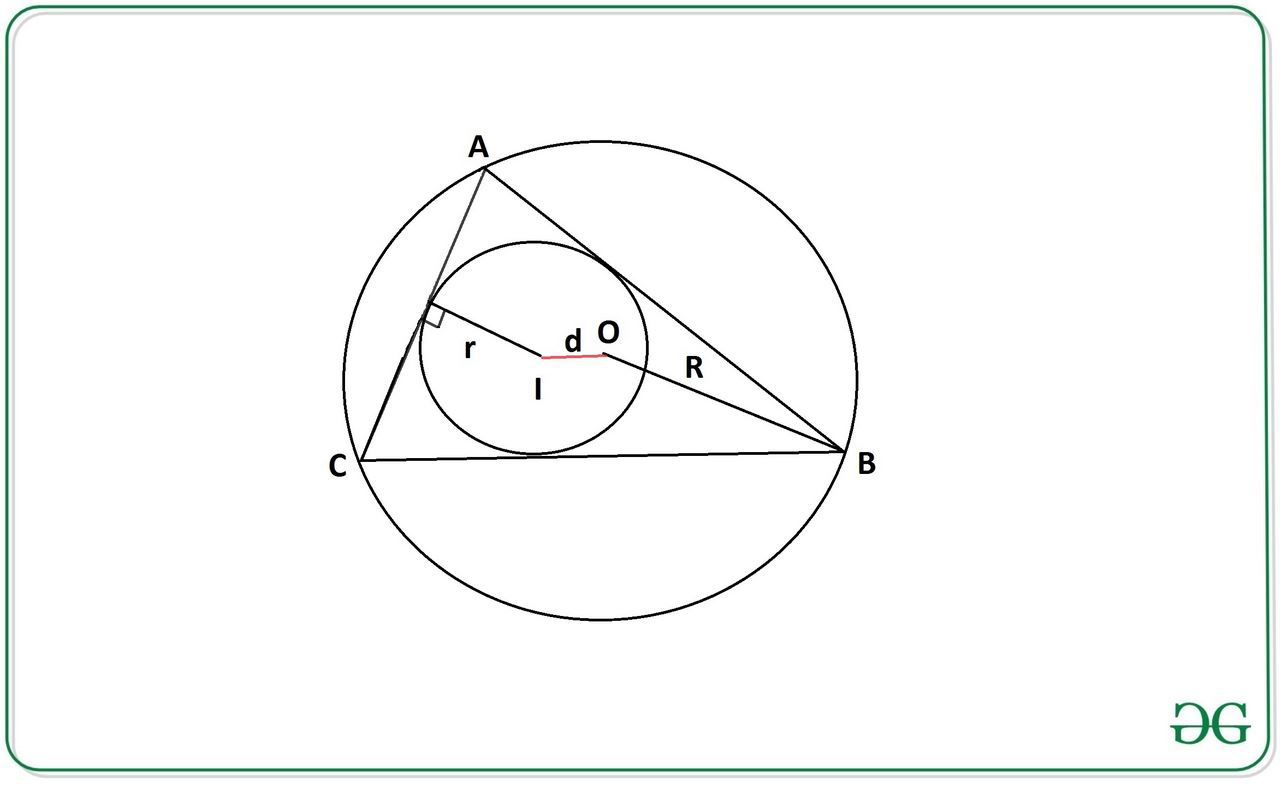
Inradius The inradius( r ) of a regular triangle( ABC ) is the radius of the incircle (having center as l), which is the largest circle that will fit inside the triangle.
Circumradius: The circumradius( R ) of a triangle is the radius of the circumscribed circle (having center as O) of that triangle.
Examples:
Input: r = 2, R = 5
Output: 2.24
Input: r = 5, R = 12
Output: 4.9
Approach:
The problem can be solved using Euler’s Theorem in geometry, which states that the distance between the incenter and circumcenter of a triangle can be calculated by the equation:
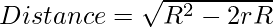
Below is the implementation of the above approach:
C++14
#include <bits/stdc++.h>
using namespace std;
double distance(int r, int R)
{
double d = sqrt(pow(R, 2) -
(2 * r * R));
return d;
}
int main()
{
int r = 2;
int R = 5;
cout << (round(distance(r, R) * 100.0) / 100.0);
}
|
Java
import java.util.*;
class GFG{
static double distance(int r,int R)
{
double d = Math.sqrt(Math.pow(R, 2) -
(2 * r * R));
return d;
}
public static void main(String[] args)
{
int r = 2;
int R = 5;
System.out.println(Math.round(
distance(r, R) * 100.0) / 100.0);
}
}
|
Python3
import math
def distance(r,R):
d = math.sqrt( (R**2) - (2 * r * R))
return d
r = 2
R = 5
print(round(distance(r,R),2))
|
C#
using System;
class GFG{
static double distance(int r, int R)
{
double d = Math.Sqrt(Math.Pow(R, 2) -
(2 * r * R));
return d;
}
public static void Main(string[] args)
{
int r = 2;
int R = 5;
Console.Write(Math.Round(
distance(r, R) * 100.0) / 100.0);
}
}
|
Javascript
<script>
function distance(r, R)
{
let d = Math.sqrt(Math.pow(R, 2) -
(2 * r * R));
return d;
}
let r = 2;
let R = 5;
document.write(Math.round(
distance(r, R) * 100.0) / 100.0);
</script>
|
Time Complexity: O(logn) since time complexity of sqrt is O(logn)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...