Distance between Incenter and Circumcenter of a triangle using Inradius and Circumradius

Given two integers r and R representing the length of Inradius and Circumradius respectively, the task is to calculate the distance d between Incenter and Circumcenter.

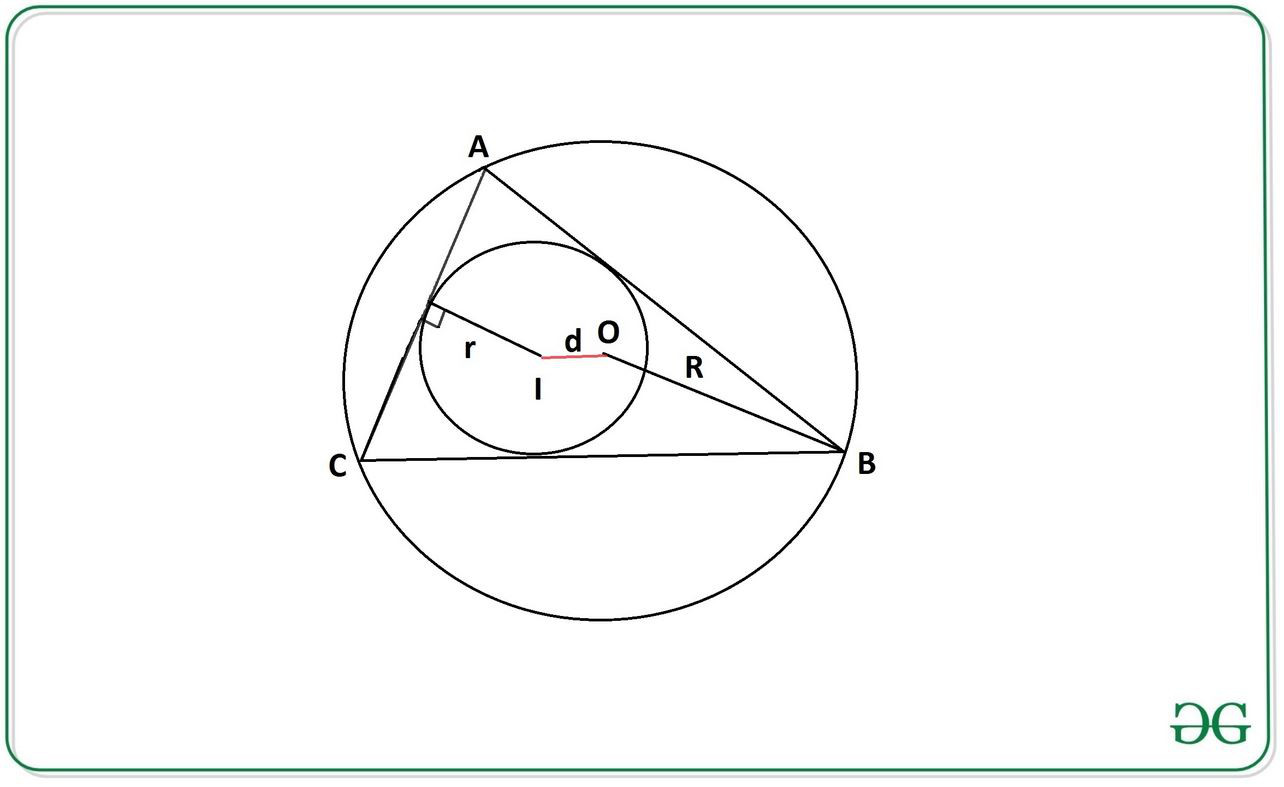
Inradius The inradius( r ) of a regular triangle( ABC ) is the radius of the incircle (having center as l), which is the largest circle that will fit inside the triangle. 
Circumradius: The circumradius( R ) of a triangle is the radius of the circumscribed circle (having center as O) of that triangle. 

Examples:

Input: r = 2, R = 5 
Output: 2.24

Input: r = 5, R = 12 
Output: 4.9

Approach:
The problem can be solved using Euler’s Theorem in geometry, which states that the distance between the incenter and circumcenter of a triangle can be calculated by the equation:

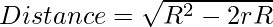
Below is the implementation of the above approach:

C++14

// C++14 program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function returns the required distance
double distance(int r, int R)
{
    double d = sqrt(pow(R, 2) -
                       (2 * r * R));

    return d;
}

// Driver code
int main()
{

    // Length of Inradius
    int r = 2;

    // Length of Circumradius
    int R = 5;

    cout << (round(distance(r, R) * 100.0) / 100.0);
}

// This code is contributed by sanjoy_62

Java

// Java program for the above approach
import java.util.*;

class GFG{

// Function returns the required distance
static double distance(int r,int R)
{
    double d = Math.sqrt(Math.pow(R, 2) -
                         (2 * r * R));

    return d;
}

// Driver code
public static void main(String[] args)
{

    // Length of Inradius
    int r = 2;

    // Length of Circumradius
    int R = 5;

    System.out.println(Math.round(
        distance(r, R) * 100.0) / 100.0);
}
}

// This code is contributed by offbeat

Python3

# Python3 program for the above approach
import math

# Function returns the required distance
def distance(r,R):

    d = math.sqrt( (R**2) - (2 * r * R))

    return d

# Driver Code

# Length of Inradius
r = 2

# Length of Circumradius
R = 5

print(round(distance(r,R),2))

C#

// C# program for the above approach
using System;

class GFG{

// Function returns the required distance
static double distance(int r, int R)
{
    double d = Math.Sqrt(Math.Pow(R, 2) -
                         (2 * r * R));

    return d;
}

// Driver code
public static void Main(string[] args)
{

    // Length of Inradius
    int r = 2;

    // Length of Circumradius
    int R = 5;

    Console.Write(Math.Round(
        distance(r, R) * 100.0) / 100.0);
}
}

// This code is contributed by rutvik_56

Javascript

<script>

// Javascript program for
// the above approach

// Function returns the required distance
function distance(r, R)
{
    let d = Math.sqrt(Math.pow(R, 2) -
                         (2 * r * R));

    return d;
}

// Driver code

    // Length of Inradius
    let r = 2;

    // Length of Circumradius
    let R = 5;

    document.write(Math.round(
        distance(r, R) * 100.0) / 100.0);

     // This code is contributed by susmitakundugoaldanga.
</script>

Output:

2.24

Time Complexity: O(logn) since time complexity of sqrt is O(logn)
Auxiliary Space: O(1)