Discrete Maths | Generating Functions-Introduction and Prerequisites

Prerequisite – Combinatorics Basics, Generalized PnC Set 1, Set 2

Definition : Generating functions are used to represent sequences efficiently by coding the terms of a sequence as coefficients of powers of a variable (say) 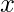$\big x$ in a formal power series.

Now with the formal definition done, we can take a minute to discuss why should we learn this concept.

This concept can be applied to solve many problems in mathematics. There is a huge chunk of mathematics dealing with just generating functions.

It can be used to solve various kinds of Counting problems easily.
It can be used to solve recurrence relations by translating the relation in terms of sequence to a problem about functions.
It can be used to prove combinatorial identities.

In simple words generating functions can be used to translate problems about sequences to problems about functions which are comparatively easy to solve using maneuvers.

Some basic prerequisites…

Before we start let’s go through some basic Combinatorics formula.

$%\documentclass{article} %\usepackage{amsmath} \newcommand*{\Perm}[2]{{}^{#1}\!P_{#2}}% \newcommand*{\Comb}[2]{{}^{#1}C_{#2}}% \begin{document} \Huge $\Perm{n}{k}=\frac{n!}{(n-k)!}$ $\binom nk=\Comb{n}{k}=\frac{n!}{k!(n-k)!}$ \end{document}$

A generating function is a “formal” power series in the sense that we usually regard x as a placeholder rather than a number. Only in rare cases will we actually evaluate a generating function by letting x take a real number value, so we generally ignore the issue of convergence.

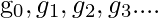$$g_0, g_1, g_2, g_3....$ of real numbers is the infinite series:
$%\documentclass{article} %\usepackage{amsmath} \begin{document} \huge \func G(x) = g_0+{g_1}x+{g_2}x^{2}..... = \sum_{k=0}^\infty g_k x^k. \end{document}$

$[g_{0},g_{1},g_{2},g_{3}...]\leftrightarrow g_{0} + g_{1}x+g_{2}x^{2}+g_{3}x^{3}....$

Note: we’ll indicate the correspondence between a sequence and its generating function with a double-sided arrow.

Some Important sequences and their results…

$\textup{Let }G_{n}=1+x+x^{2}+x^{3}+.....+x^{n-1}+x^{n}..........\hspace{1cm} eq^{n} (1)\\ \textup{Multiplying it with x } \\ xG_{n}=x+x^{2}+x^{3}+....\hspace{1cm} eq^{n} (2) \\ \\ \textup{subtracting equation (2) with (1) we will get.. } \\ G_{n}-xG_{n} =1 \\ \\G_{n}=\frac{1}{1-x}$

If you want to know more about the derivation of the given sequences you may refer here

$%\documentclass{article} %\usepackage{amsmath} \begin{document} \Large $\frac{1} {(1-x)}$ = 1 + x + x^2 + x^3.... \longleftrightarrow [1, 1, 1, 1...\normalsize\infty] \end{document}$

$%\documentclass{article} %\usepackage{amsmath} \begin{document} \Large $\frac{1} {(1+x)}$=1-x+x^2-x^3.... \longleftrightarrow [1, -1, 1, -1....\normalsize\infty] \end{document}$

$%\documentclass{article} %\usepackage{amsmath} \begin{document} \Large $\frac{1} {(1-ax)}$ = 1 + ax + {a^2}x^2 + {a^3}x^3.... \longleftrightarrow [1, a, a^2, a^3....\normalsize\infty] \end{document}$

$%\documentclass{article} %\usepackage{amsmath} \begin{document} \Large %$\frac{1} {(1-ax)}$ = 1 - ax + {a^2}x^2 - {a^3}x^3.... \longleftrightarrow [1, a, a^2, a^...\infty] $\frac{1} {(1-x^{2})}$ = 1 + x^2 + x^4.... \longleftrightarrow [1, 0, 1, 0...\normalsize\infty] \end{document}$

Note that all the above series is infinite. There is one peculiar result of finite series which will be very handy so it’s recommended to remember these results to solve problems quickly.

An important result:

$%\documentclass{article} %\usepackage{amsmath} \begin{document} \LARGE %$\frac{1} {(1-ax)}$ = 1 - ax + {a^2}x^2 - {a^3}x^3.... \longleftrightarrow [1, a, a^2, a^.....] 1+x+x^2+x^3+....+x^n = $\frac{1 + x^{n+1}} {(1-x)}$ \end{document}$

We can use these operations to get new sequences from known sequences, and new generating functions from known generating functions.

Scaling:
Multiplying a generating function by a constant scales every term in the associated sequence by the same constant.
$\textup{Scaling Rule} \newline[f_{0},f_{1},f_{2},f_{3}...]\leftrightarrow F(x) \newline [cf_{0},cf_{1},cf_{2},cf_{3}...]\leftrightarrow cF(x) \\$

$\textup{Example:} \newline [1,0,1,0,1,0...]\hspace{0.25cm}\leftrightarrow \hspace{0.25cm}1+x^{2}+x^{4}+x^{6}....\hspace{0.25cm}=\frac{1}{1-x^{2}} \\ \\ \textup{Multiplying the generating function by 2 gives}\\ \\ \frac{2}{1-x^{2}}=\hspace{0.15cm}2+2x^{2}+2x^{4}+2x^{6}..$

Addition:
Adding generating functions corresponds to adding the two sequences term by term.
$\newline[f_{0},f_{1},f_{2},f_{3},f_{4}..]\leftrightarrow F(x) \newline [g_{0},g_{1},g_{2},g_{3},g_{4}..]\leftrightarrow G(x)\newline \textup{Then}\newline [f_{0}+g_{0},f_{1}+g_{1},f_{2}+g_{2},f_{3}+g_{3},...]\leftrightarrow F(x)+G(x)$

$\textup{Example:} \newline [1,1,1,1,1,1,1,1....]\leftrightarrow \frac{1}{1-x} \hspace{1cm} \newline [1,-1,1,-1,1,-1....]\leftrightarrow \frac{1}{1+x} \newline \textup{Adding both equation we will get}\newline [2,0,2,0,2,0...]\leftrightarrow \frac{1}{1-x}+\frac{1}{1+x} \newline =\frac{2}{1-x^{2}}$

Right Shifting:
$\textup{Right Shifting Rule} \newline \textup{if}\hspace{0.25cm} [f_{0},f_{1},f_{2},f_{3}...]\leftrightarrow F(x) \newline \textup{then}\hspace{0.25cm} [\overbrace{\overset{\textup{k times}}{0,0,0,0,0,0} },f_{0},f_{1},f_{1}...]\leftrightarrow x^{k}F(x)$

$\newline \textup{Example:} \newline \newline [\overbrace{\overset{\textup{k times}}{0,0,0,0,0,0} },1,1,1,1,1,1,1...]\leftrightarrow x^{k}+x^{k+1}+x^{k+2}+x^{k+3}..... \newline \hspace{20cm} =x^{k}(1+x+x^{2}+x^{3}...) \newline \hspace{20cm}=\frac{x^{k}}{x-1}$

Differentiation:
In general, differentiating a generating function has two effects on the corresponding sequence: each term is multiplied by its index and the entire sequence is shifted left one place.
$\textup{Derivative Rule:} \newline [f_{0},f_{1},f_{2},f_{3}...] \leftrightarrow F(x) \newline [f_{1},2f_{2},3f_{3},4f_{4}...] \leftrightarrow F{}'(x)$

$\newline \textup{Example:} \newline 1+x+x^{2}+x^{3}+x^{4}+x^{5}... = \frac{1}{1-x} \newline \frac{\mathrm{d} }{\mathrm{d} x}(1+x+x^{2}+x^{3}+x^{4}...)=\frac{\mathrm{d} }{\mathrm{d} x}(\frac{1}{1-x}) \newline 1+2x+3x^{2}+4x^{3}....=\frac{1}{(1-x)^{^{2}}} \newline [1,2,3,4...]=\frac{1}{(1-x)^{2}}$

Example:
What sequence is represented by the following series :
$%\documentclass{article} %\usepackage{amsmath} \begin{document} \Large 1 + 4x^2 + x^4 + \frac{x^5}{999} + 100x^6 + \cdots\text{?} \end{document}$
SolutionBy now you must have got this, the coefficient of a₀ = 1, a₁ = 0, a₂ = 4, a₃ = 0, a₄ = 1, a₅ = 1/999, a₆ = 100.
So sequence is:
$\Large $ [1, 0, 4, 0, 1, $\frac{1} {999}$, 100, ....] $$
From the perspective of GATE CS examination, problems from this topic are asked almost every year and the problems can easily be solved just by knowing the basics.

So, with this done, from the next post, we may start with some interesting Counting Problems and solve them with this approach. We will also see some previous GATE problems.
Next, we’ll see some problems based on counting and some problems based on coefficient extraction.

REFERENCES:

Kenneth H Rosen: Discrete Mathematics and Its Applications 6^th [Chapter 2.4, 6.4]

Last Updated : 19 Feb, 2021