Usually, for three-dimensional geometry, we rely on the three-dimensional Cartesian plane. Vectors can also be used to describe the lines and the angles they make with the axis. How should we describe a line passing through origin making an angle with different axes? We define them using cosine ratios of the line. While working with three-dimensional geometry (used in so many applications such as game designing), it is required to describe the significance of the line present in 3-D space.
Direction Cosines and Direction Ratios of a Line
Let’s assume a line OA which is passing through the origin and makes angles α, β, and γ with x, y, and z-axis respectively, called direction angles. The cosines of these angles cos(α), cos(β), and cos(γ) are called directional cosines of the directed line OA. The figure given below shows the line OA passing through the origin and all the angles it makes with the coordinate axes.

Note: The line can extend in both the directions, and there can be two sets of angles that it makes with coordinate axes. The line makes α, β, and γ and their supplements 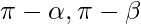 , and
, and 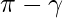 with the coordinate axes. Now the signs of the directional cosines will be reversed. So, to have unique directional cosines, we choose to make it a directed line.
with the coordinate axes. Now the signs of the directional cosines will be reversed. So, to have unique directional cosines, we choose to make it a directed line.
Let’s say the directional cosines of the lines are l, m, and n.
Direction Ratios
Numbers that are proportional to the direction cosines of the line are called direction ratios of the line. We have assumed l, m, and n as the directional cosines of the lines. Let’s say a, b and c are the directional ratios of the line. Then,
l = k × a, m = k × b and n = k × c
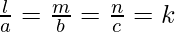
Where k is any constant.
Now we know that,
l2 + m2 + n2 = 1
⇒k2(a2 + b2 + c2) = 1
⇒ k = 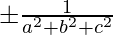
So, now the directional cosines of a line are,
l = 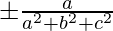 , m =
, m =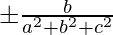 and n =
and n = 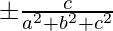
Relation between Directional Cosines
Let’s assume we have a line BC that has directional cosines l, m, and n. Draw a line through the origin that is parallel to this line and let’s take A(x, y, z) a point on this line. We draw a perpendicular from A to the x-axis.

Let OA = r.
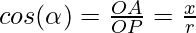
So, x = lr and similarly, y = mr and z = nr.

x2 + y2 + z2 = r2(l2 + m2 + n2)
We know that distance of (x, y,z) from origin is r.
x2 + y2 + z2 = r2
Thus,
l2 + m2 + n2 = 1
Direction cosines of the lines passing through two points
Imagine we have two points A(x1,y1,z1) and B(x2, y2, z2) and a line passes through them. Our goal is to determine the directional cosines of the line that is passing through these points. Let l, m, and n be the directional cosines of the line AB and let’s say the angles they make with the x,y and z axes respectively are α, β, and γ.

In the figure given above, perpendiculars are drawn from the line AB to the XY plane, and they reach the XY plane at CD. Another perpendicular should be drawn from A to BD which meets BD and N. So, now in the triangle ANB, ∠ABN is γ.

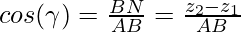
In the same way,
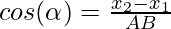 and
and 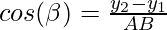
So, the directional cosines of the line joining AB are,
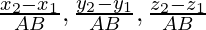
Here, AB = 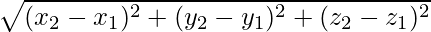
Let’s see some sample problems based on these concepts,
Sample Problems
Question 1: Find the directional cosines of the x, y, and z-axis.
Solution:
The x-axis makes an angle of 90°, 90° and 0° with the coordinate axes. We know that the direction cosines are basically cosines of the angle the line makes with different axes.
l = cos(0°) m = cos(90°) and n = cos(90°)
Thus,
l = 1, m = n = 0
Similarly, for y-axis,
l = 0, m = 1 and n = 0
and for z-axis
l = 0, m = 0 and n = 1.
Question 2: Find the directional cosines for a line that makes 30°, 60°, and 90° with the x, y, and z axes respectively.
Solution:
Directional cosines for the given line are,
l = cos(30°) ; m = cos(60°) and n = cos(90°)
⇒ l = 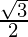 ; m =
; m = 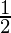 and n = 0
and n = 0
Question 3: Let’s say we have a line with direction ratios 4, 2, -4. Calculate the direction cosines for this line.
Solution:
Given direction ratios: 4, 2, and -4.
The formula for directional cosines from direction ratios is given by,
l =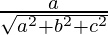 , m =
, m =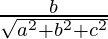 and n =
and n = 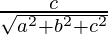
Here, a = 4, b = 2 and c =-4.
l = 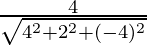 , m =
, m =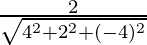 and n =
and n = 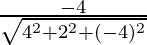
l = \frac{4}{\sqrt{36}}
m = 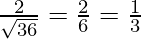
n = 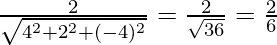
Question 4: Let’s say we have a line with direction ratios 0, 1, 0. Calculate the direction cosines for the line.
Solution:
Given direction ratios: 0, 1, and 0.
The formula for directional cosines from direction ratios is given by,
l =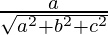 , m =
, m =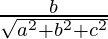 and n =
and n = 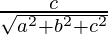
Here, a = 0, b = 1 and c =0.
l = 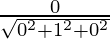 , m =
, m =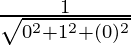 and n =
and n = 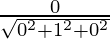
l = 0
m = 1
n = 0
Question 5: Find the direction cosines of the lines passing through (1, 1, 1) and (3, 3, 3).
Solution:
Let’s say these points are A(1,1,1) and B(3,3,3). We know for any two points on the line AB, the direction cosines are given by,
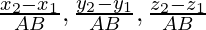
Here, AB = 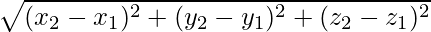
Here, (x1,y1,z1) = (1,1,1) and (x2,y2,z2) = (3,3,3)
AB = 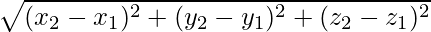
= 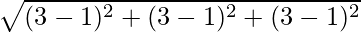
= 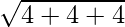
= 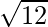
= 2√3
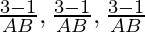
⇒ 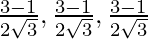
⇒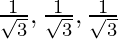
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...