Direct Address Table

Direct Address Table is a data structure that has the capability of mapping records to their corresponding keys using arrays. In direct address tables, records are placed using their key values directly as indexes. They facilitate fast searching, insertion and deletion operations. 

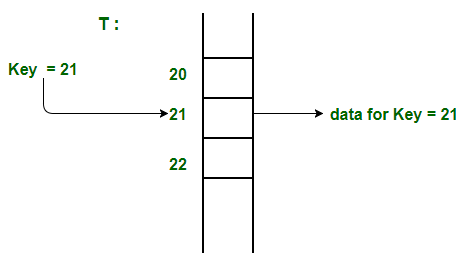
We can understand the concept using the following example. We create an array of size equal to maximum value plus one (assuming 0 based index) and then use values as indexes. For example, in the following diagram key 21 is used directly as index. 

Advantages:

1. Searching in O(1) Time: Direct address tables use arrays which are random access data structure, so, the key values (which are also the index of the array) can be easily used to search the records in O(1) time.
2. Insertion in O(1) Time: We can easily insert an element in an array in O(1) time. The same thing follows in a direct address table also.
3. Deletion in O(1) Time: Deletion of an element takes O(1) time in an array. Similarly, to delete an element in a direct address table we need O(1) time.

Limitations:

1. Prior knowledge of maximum key value
2. Practically useful only if the maximum value is very less.
3. It causes wastage of memory space if there is a significant difference between total records and maximum value.

Hashing can overcome these limitations of direct address tables. 

How to handle collisions?
Collisions can be handled like Hashing. We can either use Chaining or open addressing to handle collisions. The only difference from hashing here is, we do not use a hash function to find the index. We rather directly use values as indexes.