Dipole in a Uniform Magnetic Field

The magnetic field lines produced by the magnet are represented by the pattern of iron filings. We may get a rough estimate of the magnetic field B by looking at these magnetic field lines. However, we are frequently called upon to precisely measure the magnitude of the magnetic field B. We do this by placing a small compass needle in the magnetic field with a known magnetic moment m and moment of inertia and allowing it to oscillate. Let’s take a closer look at the concept!

A magnetic dipole is often a tiny magnet with atomic or subatomic dimensions, analogous to an electric charge flow around a loop. Spinning positively charged atomic nuclei, electrons rotating on their axes, and electrons travelling around atomic nuclei are all magnetic dipoles.

These effects may cancel one other out, resulting in a certain form of an atom that is not a magnetic dipole. The atom is an everlasting magnetic dipole if they do not totally cancel out. Iron atoms, for example, are dipoles. A magnetic dipole is formed when millions of iron atoms spontaneously lock into the same arrangement, forming a ferromagnetic domain. Macroscopic magnetic dipoles include things like magnetic compass needles and bars.

Consider a magnet bar (N-S) with a length of 2ļ and a pole strength of m in a uniform magnetic field of induction indicated as B by creating an angle θ. The first force (m × B) acts on the North Pole in the direction of the magnetic field, while the second force (m × B) acts on the South Pole in the opposite direction of the magnetic field. These two new forces are the same and the opposite of each other. As a result, a couple is created.

Uniform Field Torque on a Magnetic Dipole

The North Pole detects a force equal to the multiplication of the magnetic field intensity and the pole strength in the magnetic field direction when a magnetic rod (which can be regarded as a magnetic dipole) is kept in a uniform magnetic field.

Nonetheless, the South Pole detects an equal-but-opposite-direction force. As a result, a torque is applied to the magnetic dipole, causing it to rotate. Because the pair is the torque is denoted by τ.

τ = Force × Distance

∴ τ = F × NA

We have, F = m × B

So, =  mB × 2ļ sin θ = MB sin θ

In vector Form,

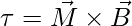
Perpendicular to the plane in the direction of τ.  

If θ = 90^o and B = 1.

Then, τ = MB sin θ = M

As a result, the magnetic moment induction equals the torque required to hold the magnet at 90 degrees with a magnetic field.

Electrostatic Analog – Compare the equation of an electric dipole in an electric field with the equation of an electric dipole in a magnetic field. The magnetic field produced by a bar magnet at a great distance is equivalent to an electric dipole in an electric field, we conclude. Similarly, as shown below, the relationship might have a status.

E → B, p → m, 1/4πε₀ → μ₀/4π

If the value of r, that is, the distance between a point and a particular magnet, is relatively great in comparison to the size of the magnet provided by I, or r >> l, the equatorial field created by a bar magnet can be written as,

B_E = −μ₀m/4πr³

Similarly, in the same condition, the axial field of the bar magnet can be expressed as,

B_A = −μ₀2m/4πr³

Dipole in a Uniform Magnetic Field

A magnetic moment is a measurement of a magnet’s magnetic strength and orientation, as well as any other object’s magnetic field. A magnetic moment is more accurately referred to as a magnetic dipole moment, which is the component of the magnetic moment that may be represented by a magnetic dipole. In a magnetic dipole, two magnetic north poles are separated by a little distance.

A magnetic dipole is made up of two poles that are diametrically opposed and separated by a small distance.

Bar magnets, compass needles, and other items are magnetic dipoles. The behaviour of a current loop will be compared to that of a magnetic dipole. Because electrons revolve around the nucleus, an atom of a magnetic substance behaves like a dipole. The north and south poles of a magnetic dipole (or magnet) are always of equal strength and opposite type. Furthermore, two magnetic poles of this type are always found in pairs and cannot be separated. The magnetic length of a bar magnet is determined by the distance between its two poles. It’s a vector that travels from the S-pole to the N-pole of a magnet, and it’s represented by the number 2ļ.

Magnetic Dipole Moment = Strength of either pole × Magnetic length

M = m(2l)

The magnetic dipole moment is a vector quantity that runs from the south pole to the north pole of the magnet, as shown in the diagram.

The unit of M is joule/tesla or ampere meter². The pole strength unit in SI is the A-m.

Bar magnet as an equivalent solenoid

A current loop is known to function in a magnetic dipole. All magnetic phenomena can be explained in terms of circulating currents, according to Ampere’s theory.

The magnetic field lines of a bar magnet and a current-carrying solenoid are remarkably similar in the figure. As a result, a bar magnet, like a solenoid, can be conceived of as a huge number of circulating currents. In the same way that a solenoid may be severed, a bar magnet can be severed. Two smaller solenoids, each with weaker magnetic characteristics, are provided. In a continuous loop, magnetic field lines emanate from one solenoid’s face and enter the second solenoid’s face. When a small compass needle is moved near a bar magnet and a current-carrying solenoid, the needle deflections are similar in both circumstances.

To demonstrate how a current-carrying finite solenoid is equivalent to a bar magnet, calculate the axial field of a current-carrying finite solenoid.

In figure, suppose: a = the solenoid’s radius, 2l = Solenoid length with center O, n = amount of solenoid turns per unit length, i = the current strength that went through the solenoid

The magnetic field must be determined at any point P on the solenoid’s axis, where OP = r. Consider a tiny solenoid with a thickness of dx and a distance from O of x.

n dx = the element’s number of turns.

The magnitude of the magnetic field at P due to this current element can be calculated using Equation.

dB = (μ₀ia²(n dx)) / (2[(r-x)²+a²]^3/2)

If P is located at a large distances from O, i.e., r>>a and r>>x, then [(r-x)²+a²]^3/2 ≈ r³

dB = (μ₀ia²ndx) / (2r³)

As range of variation of x if from -l to +l. As a result, the magnitude of the entire magnitude field at P as a result of the current-carrying solenoid is

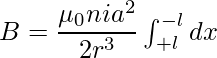
∴ B =  μ₀ni/2 × a²/r³ (2l)

∴ B = μ₀/4π × 2n(2l)i π a²/r³

If M is the magnetic moment of the solenoid, then

M = Total number of turns × current × area of cross section 

M = n(2l) × i × (π a²)

∴ B = (μ/4π)(2M/r³) 

It’s how the magnetic field on the axial line of a tiny bar magnet is expressed. As a result, the axial field of a current-carrying finite solenoid is equivalent to that of a bar magnet. As a result, a current-carrying finite solenoid is equivalent to a bar magnet in terms of functionality.

Potential energy of a magnetic dipole in a magnetic field

A magnetic dipole’s potential energy in a magnetic field is the energy that the dipole has due to its unique position in the field. When a magnetic dipole of moment M is held at an angle θ to the direction of a homogeneous magnetic field B, the magnitude of the torque acting on it equals

τ = MBsinθ

As a result of the torque, the dipole aligns in the field’s direction. Work is required to rotate the dipole against the torque’s action. This work is stored as dipole potential energy by the magnetic dipole.

A tiny amount of work is now necessary to rotate the dipole at a slight angle dθ against the restoring torque.

dW = τdθ = MBsinθ dθ

Total work done in rotating the dipole from θ₁ = θ to θ = θ₂ is

∴ W = -MB[cosθ₂ – cosθ₁]

∴ Dipole’s Potential energy is

U = W = -MB[cosθ₂ – cosθ₁]

If θ₁ = 90^o and θ₂ = θ, then

U = W = -MB[cosθ – cos90^o]

∴ U = W = -MBcosθ

∴ W = -MBcosθ

In vector notation,

U = -M^‘B^‘

Particular Cases

• When θ = 90^o

We have,

U =  -MBcosθ

∴ U = -MBcos90^o

∴ U = 0

i.e. a dipole’s potential energy is zero when it is perpendicular to the magnetic field.

As a result, we use it to determine the potential energy of a dipole at any angle with B.

U =  -MB(cos θ₂ – cos θ₁)

And take θ₁ = 90^o and θ₂ = θ.

Therefore,

U = -MB(cos θ – cos 90^o)

∴ U = -MBcosθ

• When θ = 0^o

we have,

U =  -MBcosθ

∴ U = -MBcos0^o

∴ U = -MB

Which is minimum.

This is the point of stable equilibrium where the magnetic dipole is oriented along the magnetic field and has the minimum P.E.

• When θ = 180^o

we have,

U =  -MBcosθ

∴ U = -MBcos180^o

∴ U = MB

Which is maximum.

This is the unstable equilibrium point.

Sample Problems

Problem 1: In an external magnetic field B = (0.2 i + 0.2 j – 0.3 k), a planar coil of area 7 m² carrying an anti-clockwise current 2 A is positioned such that the normal to the plane is along the line (3 i – 5 j +4 k). Find the potential energy for this case.

Solution:

Given : A = 7 m, n = 1/√50(3 i – 5 j +4 k) ≅ 1/7(3 i – 5 j +4 k)

A = (3 i – 5 j +4 k)m²

B = (0.2 i + 0.2 j – 0.3 k)T, I = 2A

Since, 

M = IA

∴ M = (6 i – 10 j + 8 k)Am²

∴ M ≅ 14Am²

U = MB

∴ U = -[1.2 – 2 – 2.4]

∴ U = 3.2 J

Problem 2: The radius of an electron’s orbit around the nucleus in an atom is 0.53 Ă. If the electron’s frequency of revolution is 6.8 × 10⁹ MHz, find the comparable magnetic moment.

Solution”

Given : e = 1.6 × 10^-19, f = 6.8 × 10⁹, r = 0.53 × 10^-10

Solution :

M = NIA = IA = Qfa

∴ M = 1.6 × 10^-19 × 6.8 × 10⁹ × 10⁶ × π × 0.53 × 10^-10

∴ M = 18.10 × 10^-14 Am²

Problem 3: Write the formula for the magnetic potential energy of a magnetic dipole in a homogeneous magnetic field.

Solution:

The formula for the magnetic potential energy of a magnetic dipole in a homogeneous magnetic field

U = -M’B’

where, 

• U = Magnetic Potential energy,
• M = The magnetic dipole’s magnetic moment,
• B = Uniform magnetic field.

Problem 4: The electron in a hydrogen atom revolves at a rate of 10¹⁶ revolutions per second in an orbit with a radius of 0.6 Ă. The magnetic moment associated with the electron’s orbital motion is

Solution:

Given : e = 1.6 × 10^-19, T = 1, r = 0.6 × 10^-10

Since, 

I = q/T = e/T

∴ I = 1.6 × 10^-19 × 10¹⁶ / 1

∴ I = 1.6 × 10^-3

M = IA

∴ M = 1.6 × 10^-3 × πr²

∴ M = 1.6 × 10^-3 × 3.14 × (0.6 × 10^-10)²

∴ M = 1.8086 × 10^-23

Problem 5: In an external magnetic field B, a circular current loop with magnetic moment M is oriented in any direction. Determine the work done required to rotate the loop by 30 degrees around an axis perpendicular to its plane.

Solution:

The work done to rotate the loop by 30 degree about an axis perpendicular to its plane results in no change in the angle formed by the loop’s axis with the direction of the magnetic field, hence the work done to rotate the loop is zero.

W = -MB[cosθ₂ – cosθ₁]

Problem 6: A charged particle (charge q) moves at a constant speed v in a circle of radius R. Then what is the accompanying magnetic moment?

Solution:

Because of the movement in a circle, the current in a circular path is provided by

i = q/T

∴ i = qv/2πR

As a result, the magnetic moment of the particle is

μ = iA

∴ μ = qv/2πR × πR²

∴ μ = qvR/2