Dijkstra’s shortest path algorithm using set in STL
Last Updated :
16 Oct, 2023
Given a graph and a source vertex in graph, find shortest paths from source to all vertices in the given graph.
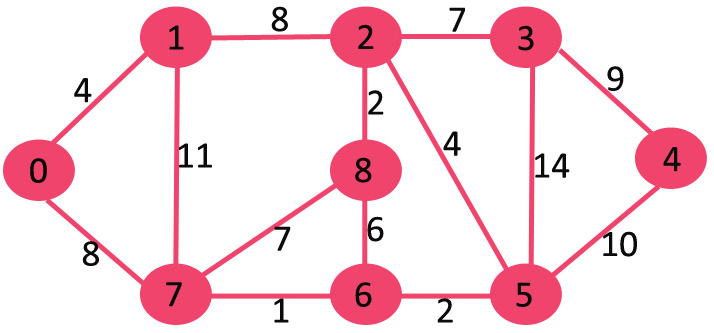
Input : Source = 0
Output :
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
We have discussed Dijkstra’s shortest Path implementations.
The second implementation is time complexity wise better, but is really complex as we have implemented our own priority queue. STL provides priority_queue, but the provided priority queue doesn’t support decrease key and delete operations. And in Dijkstra’s algorithm, we need a priority queue and below operations on priority queue :
- ExtractMin : from all those vertices whose shortest distance is not yet found, we need to get vertex with minimum distance.
- DecreaseKey : After extracting vertex we need to update distance of its adjacent vertices, and if new distance is smaller, then update that in data structure.
Above operations can be easily implemented by set data structure of c++ STL, set keeps all its keys in sorted order so minimum distant vertex will always be at beginning, we can extract it from there, which is the ExtractMin operation and update other adjacent vertex accordingly if any vertex’s distance becomes smaller then delete its previous entry and insert new updated entry which is DecreaseKey operation.
Below is algorithm based on set data structure.
1) Initialize distances of all vertices as infinite.
2) Create an empty set. Every item of set is a pair
(weight, vertex). Weight (or distance) is used
as first item of pair as first item is by default
used to compare two pairs.
3) Insert source vertex into the set and make its
distance as 0.
4) While Set doesn't become empty, do following
a) Extract minimum distance vertex from Set.
Let the extracted vertex be u.
b) Loop through all adjacent of u and do
following for every vertex v.
// If there is a shorter path to v
// through u.
If dist[v] > dist[u] + weight(u, v)
(i) Update distance of v, i.e., do
dist[v] = dist[u] + weight(u, v)
(i) If v is in set, update its distance
in set by removing it first, then
inserting with new distance
(ii) If v is not in set, then insert
it in set with new distance
5) Print distance array dist[] to print all shortest
paths.
Below is the implementation of above idea.
C++
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f
class Graph
{
int V;
list< pair<int, int> > *adj;
public:
Graph(int V);
void addEdge(int u, int v, int w);
void shortestPath(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list< pair<int, int> >[V];
}
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(make_pair(v, w));
adj[v].push_back(make_pair(u, w));
}
void Graph::shortestPath(int src)
{
set< pair<int, int> > setds;
vector<int> dist(V, INF);
setds.insert(make_pair(0, src));
dist[src] = 0;
while (!setds.empty())
{
pair<int, int> tmp = *(setds.begin());
setds.erase(setds.begin());
int u = tmp.second;
list< pair<int, int> >::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
{
int v = (*i).first;
int weight = (*i).second;
if (dist[v] > dist[u] + weight)
{
if (dist[v] != INF)
setds.erase(setds.find(make_pair(dist[v], v)));
dist[v] = dist[u] + weight;
setds.insert(make_pair(dist[v], v));
}
}
}
printf("Vertex Distance from Source\n");
for (int i = 0; i < V; ++i)
printf("%d \t\t %d\n", i, dist[i]);
}
int main()
{
int V = 9;
Graph g(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.shortestPath(0);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class Graph {
private int V;
private List<PriorityQueue<Node>> adj;
public Graph(int V) {
this.V = V;
adj = new ArrayList<>(V);
for (int i = 0; i < V; ++i)
adj.add(new PriorityQueue<>(Comparator.comparingInt(node -> node.weight)));
}
public void addEdge(int u, int v, int w) {
adj.get(u).add(new Node(v, w));
adj.get(v).add(new Node(u, w));
}
public void shortestPath(int src) {
Set<Node> setds = new HashSet<>();
int[] dist = new int[V];
Arrays.fill(dist, Integer.MAX_VALUE);
setds.add(new Node(src, 0));
dist[src] = 0;
while (!setds.isEmpty()) {
Node tmp = setds.iterator().next();
setds.remove(tmp);
int u = tmp.vertex;
for (Node neighbor : adj.get(u)) {
int v = neighbor.vertex;
int weight = neighbor.weight;
if (dist[v] > dist[u] + weight) {
setds.remove(new Node(v, dist[v]));
dist[v] = dist[u] + weight;
setds.add(new Node(v, dist[v]));
}
}
}
System.out.println("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
System.out.println(i + "\t\t" + dist[i]);
}
private static class Node {
int vertex;
int weight;
public Node(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
}
}
public class GFG {
public static void main(String[] args) {
int V = 9;
Graph g = new Graph(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.shortestPath(0);
}
}
|
Python3
import heapq
class Graph:
def __init__(self, V):
self.V = V
self.adj = [[] for _ in range(V)]
def addEdge(self, u, v, w):
self.adj[u].append((v, w))
self.adj[v].append((u, w))
def shortestPath(self, src):
pq = [(0, src)]
dist = [float('inf')] * self.V
dist[src] = 0
while pq:
d, u = heapq.heappop(pq)
if d > dist[u]:
continue
for v, weight in self.adj[u]:
if dist[v] > dist[u] + weight:
dist[v] = dist[u] + weight
heapq.heappush(pq, (dist[v], v))
print("Vertex Distance from Source")
for i in range(self.V):
print(f"{i} \t\t {dist[i]}")
if __name__ == "__main__":
V = 9
g = Graph(V)
g.addEdge(0, 1, 4)
g.addEdge(0, 7, 8)
g.addEdge(1, 2, 8)
g.addEdge(1, 7, 11)
g.addEdge(2, 3, 7)
g.addEdge(2, 8, 2)
g.addEdge(2, 5, 4)
g.addEdge(3, 4, 9)
g.addEdge(3, 5, 14)
g.addEdge(4, 5, 10)
g.addEdge(5, 6, 2)
g.addEdge(6, 7, 1)
g.addEdge(6, 8, 6)
g.addEdge(7, 8, 7)
g.shortestPath(0)
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
class Graph {
private int V;
private List<Tuple<int, int> >[] adj;
public Graph(int V)
{
this.V = V;
adj = new List<Tuple<int, int> >[ V ];
for (int i = 0; i < V; i++) {
adj[i] = new List<Tuple<int, int> >();
}
}
public void AddEdge(int u, int v, int w)
{
adj[u].Add(Tuple.Create(v, w));
adj[v].Add(Tuple.Create(u, w));
}
public void ShortestPath(int src)
{
SortedSet<Tuple<int, int> > setds
= new SortedSet<Tuple<int, int> >();
int[] dist
= Enumerable.Repeat(int.MaxValue, V).ToArray();
setds.Add(Tuple.Create(0, src));
dist[src] = 0;
while (setds.Count > 0) {
Tuple<int, int> tmp = setds.First();
setds.Remove(tmp);
int u = tmp.Item2;
foreach(var edge in adj[u])
{
int v = edge.Item1;
int weight = edge.Item2;
if (dist[v] > dist[u] + weight) {
if (dist[v] != int.MaxValue) {
setds.Remove(
Tuple.Create(dist[v], v));
}
dist[v] = dist[u] + weight;
setds.Add(Tuple.Create(dist[v], v));
}
}
}
Console.WriteLine("Vertex Distance from Source");
for (int i = 0; i < V; ++i) {
Console.WriteLine(i + "\t\t" + dist[i]);
}
}
}
class Program {
public static void Main()
{
int V = 9;
Graph g = new Graph(V);
g.AddEdge(0, 1, 4);
g.AddEdge(0, 7, 8);
g.AddEdge(1, 2, 8);
g.AddEdge(1, 7, 11);
g.AddEdge(2, 3, 7);
g.AddEdge(2, 8, 2);
g.AddEdge(2, 5, 4);
g.AddEdge(3, 4, 9);
g.AddEdge(3, 5, 14);
g.AddEdge(4, 5, 10);
g.AddEdge(5, 6, 2);
g.AddEdge(6, 7, 1);
g.AddEdge(6, 8, 6);
g.AddEdge(7, 8, 7);
g.ShortestPath(0);
}
}
|
Javascript
const INF = 0x3f3f3f3f;
class Graph {
constructor(V) {
this.V = V;
this.adj = new Array(V);
for (let i = 0; i < V; i++) {
this.adj[i] = [];
}
}
addEdge(u, v, w) {
this.adj[u].push({ v, w });
this.adj[v].push({ u, w });
}
shortestPath(src) {
const setds = new Set();
const dist = new Array(this.V).fill(INF);
setds.add([0, src]);
dist[src] = 0;
while (setds.size !== 0) {
const tmp = setds.values().next().value;
setds.delete(tmp);
const u = tmp[1];
for (const i of this.adj[u]) {
const { v, w } = i;
if (dist[v] > dist[u] + w) {
if (dist[v] !== INF) {
setds.delete([dist[v], v]);
}
dist[v] = dist[u] + w;
setds.add([dist[v], v]);
}
}
}
console.log("Vertex Distance from Source");
for (let i = 0; i < this.V; i++) {
console.log(`${i} \t\t ${dist[i]}`);
}
}
}
function main() {
const V = 9;
const g = new Graph(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.shortestPath(0);
}
main();
|
Output
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
Time Complexity: Set in C++ are typically implemented using Self-balancing binary search trees. Therefore, time complexity of set operations like insert, delete is logarithmic and time complexity of above solution is O(ELogV)).
Space Complexuty:O(V2) , here V is number of Vertices.
Dijkstra’s Shortest Path Algorithm using priority_queue of STL
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...