Functional Completeness in Digital Logic
Last Updated :
11 May, 2023
A set of operations is said to be functionally complete or universal if and only if every switching function can be expressed by means of operations in it. A set of Boolean functions is functionally complete, if all other Boolean functions can be constructed from this set and a set of input variables are provided, e.g.
- Set A = {+,*,’ (OR, AND, complement) } are functionally complete.
- Set B = {+,’} are functionally complete
- Set C = {*,’} are functionally complete
Post’s Functional Completeness Theorem – Important closed classes of functions:
- T0 – class of all 0-preserving functions, such as f(0, 0, … , 0) = 0.
- T1 – class of all 1-preserving functions, such as f(1, 1, … , 1) = 1.
- S – class of self-dual functions, such as f(x1, … ,xn) = ¬ f(¬x1, … , ¬xn).
- M – class of monotonic functions, such as : {x1, … ,xn} ? {x1, … ,xn}, if xi ? yi if {x1, … ,xn} ? {x1, … ,xn} then f(x1, … ,xn) ? f(x1, … ,xn)
- L – class of linear functions, which can be presented as: f(x1, … ,xn) = a0 + a1·x1 + … + an·xn ; ai {0, 1}.
Theorem – A system of Boolean functions is functionally complete if and only if for each of the five defined classes T0, T1, S, M, L, there is a member of F which does not belong to that class. These are minimal functionally complete operator sets – One element – {?}, {?}. Two elements – 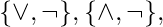 [Tex]{\displaystyle \{\to ,\neg \}}, {\displaystyle \{\gets ,\neg \}}, [/Tex]
[Tex]{\displaystyle \{\to ,\neg \}}, {\displaystyle \{\gets ,\neg \}}, [/Tex]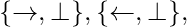 [Tex]{\displaystyle \{\to ,\nleftrightarrow \}}, {\displaystyle \{\gets ,\nleftrightarrow \}}, [/Tex]
[Tex]{\displaystyle \{\to ,\nleftrightarrow \}}, {\displaystyle \{\gets ,\nleftrightarrow \}}, [/Tex]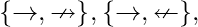 [Tex]{\displaystyle \{\gets ,\nrightarrow \}}, {\displaystyle \{\gets ,\nleftarrow \}}, [/Tex]
[Tex]{\displaystyle \{\gets ,\nrightarrow \}}, {\displaystyle \{\gets ,\nleftarrow \}}, [/Tex]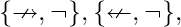 [Tex]{\displaystyle \{\nrightarrow ,\top \}}, {\displaystyle \{\nleftarrow ,\top \}}, [/Tex]
[Tex]{\displaystyle \{\nrightarrow ,\top \}}, {\displaystyle \{\nleftarrow ,\top \}}, [/Tex]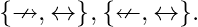 Three elements –
Three elements – 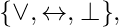 [Tex]{\displaystyle \{\lor ,\leftrightarrow ,\nleftrightarrow \}}, [/Tex]
[Tex]{\displaystyle \{\lor ,\leftrightarrow ,\nleftrightarrow \}}, [/Tex]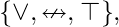 [Tex]{\displaystyle \{\land ,\leftrightarrow ,\bot \}}, [/Tex]
[Tex]{\displaystyle \{\land ,\leftrightarrow ,\bot \}}, [/Tex]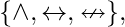 [Tex]{\displaystyle \{\land ,\nleftrightarrow ,\top \}}. [/Tex]Examples on functional Completeness –
[Tex]{\displaystyle \{\land ,\nleftrightarrow ,\top \}}. [/Tex]Examples on functional Completeness –
- Check if function F(A,B,C) = A’+BC’ is functionally complete?
- Explanation – Let us start by putting all variables as ‘A’ so it becomes F(A,A,A) = A’+A.A’ = A’—-(i) F(B,B,B) = B’+B.B’ = B’—(ii) Now substitute F(A,A,A) in place of variable ‘A’ and F(B,B,B) in place of variable ‘C’ F(F(A,A,A),B,F(B,B,B)) = (A’)’+B.(B’)’ = A+B—(iii) from (i) and (ii) complement is derived and from (iii) operator ‘+’ is derived so this function is functionally complete as from above if function contains {+,’} is functionally complete.
- Check if function F(A,B) = A’+B is functionally complete?
- Explanation – Let us start by putting all variables as ‘A’ so it becomes F(A,A) = A’+A = 1—-(i) F(B,B) = B’+B = 1—(ii) F(A,0) = A’+0 = A’—(iv) Now substitute F(A,0) in place of variable ‘A’ F(F(A,0),B) = (A’)’+B = A+B—(iii) from (iv) complement is derived and from (iii) operator ‘+’ is derived so this function is functionally complete as from above if function contains {+,’} is partially functionally complete .
- Check if function F(A,B) = A’B is functionally complete?
- Explanation – Let us start by putting all variables as ‘A’ so it becomes F(A,A) = A’.A’ = 0—-(i) F(A,0) = A’.0 = 0—(ii) F(A,1) = A’.1 = A’—(iv) Now substitute F(A,1) in place of variable ‘A’ F(F(A,1),B) = (A’)’*B = A*B—(iii) from (iv) complement is derived and from (iii) operator ‘*’ is derived so this function is functionally complete as from above if function contains {*,’} is partially functionally complete . Note – If the function becomes functionally complete by substituting ‘0’ or ‘1’ then it is known as partially functionally complete.
- Check if function F(A,B) = A’B+AB’ (EX-OR) is functionally complete?
- Explanation – Let us start by putting all variables as ‘A’ so it becomes F(A,1) = A’.1 + A.0 = A’—-(i) F(A’,B) = AB + A’B’–(ii) F(A’,B’) = AB’ + A’B–(iii) F(A,B’) = A’B’ + AB—(iv) So there is no way to get {+,*,’} according to condition. So EX-OR is non functionally complete .
- Consider the operations f(X, Y, Z) = X’YZ + XY’ + Y’Z’ and g(X?, Y, Z) = X?YZ + X?YZ? + XY Which one of the following is correct? (A) Both {f} and {g} are functionally complete (B) Only {f} is functionally complete (C) Only {g} is functionally complete (D) Neither {f} nor {g} is functionally complete
Advantages of Functional Completeness:
Flexibility: A functionally complete set of logical operations can represent any boolean function, which makes it a flexible and powerful tool for digital logic design.
Efficiency: A functionally complete set of logical operations can be implemented using a small number of basic gates, which makes it an efficient and cost-effective approach for implementing digital circuits.
Universality: A functionally complete set of logical operations is universal, which means that it can be used in any application that requires digital logic design.
Disadvantages of Functional Completeness:
Complexity: Functionally complete sets of logical operations can be complex and difficult to understand, especially for beginners in digital logic design.
Limited Applicability: Functionally complete sets of logical operations may not be suitable for all digital logic design applications. Some applications may require specialized operations or functions that are not represented by functionally complete sets.
Non-Intuitiveness: Functionally complete sets of logical operations can be difficult to use and interpret because they are based on abstract mathematical concepts rather than intuitive concepts.
References – Post’s Functional Completeness Theorem Functional completeness – Wikipedia
Share your thoughts in the comments
Please Login to comment...