Derivative of Inverse Trig Function refers to the rate of change in Inverse Trigonometric Functions. We know that the derivative of a function is the rate of change in a function with respect to the independent variable. Before learning this one should know the formulas of differentiation of Trigonometric Functions. To find the derivative of the Inverse Trigonometric Function, we will first equate the trigonometric function with another variable to find its inverse and then differentiate it using the implicit differentiation formula.
In this article, we will learn the Derivative of Inverse Trig Functions, Formulas of Differentiation of Inverse Trig Functions, and Solve some Examples based on it. But before heading forward, let’s brush up on the concept of inverse trigonometric functions and implicit differentiation.
Inverse Trigonometric Functions
Inverse Trigonometric Functions are the inverse functions of the trigonometric ratios i.e. sin, cos, tan, cot, sec, cosec. These functions are widely used in fields like physics, mathematics, engineering, and other research fields. Just like addition and subtraction are the inverses of each other, the same is true for the inverse of trigonometric functions.
sin θ = x
⇒ θ = sin−1x
Representation of Inverse Trigonometric Functions
They are represented by adding arc in prefix or by adding -1 to the power.
Inverse sine can be written in two ways:
Same goes for cos and tan.
Note: Don’t confuse sin-1 x with (sin x)-1. They are different. Writing sin-1 x is a way to write inverse sine whereas (sin x)-1 means 1/sin x.
Domain of Inverse Trigonometric Functions
We know that a function is differentiable only if it is continuous at that point and if a function is continuous at a given point then that point is the domain of the function. Hence we should learn the domain of the inverse trigonometric functions for the same.
|
sin-1x
| [-1, 1]
|
cos-1x
| [-1, 1]
|
tan-1x
| R
|
cosec-1x
| (-∞, -1]∪[1, ∞)
|
sec-1x
| (-∞, -1]∪[1, ∞)
|
cot-1x
| R
|
Now let’s learn the technique of implicit differentiation briefly.
What is Implicit Differentiation?
Implicit differentiation is a method that makes use of the chain rule to differentiate implicitly defined functions. An implicit functions is the function which contains two variable rather than one variable. In such case sometimes we can convert the function into one variable explicitly but this not the case always. Since, it is generally not easy to find the function explicitly and then differentiate. Instead, we can totally differentiate f(x, y) i.e. both the variables and then solve the rest of the equation to find the value of f'(x).
What is Derivative of Inverse Trigonometric Functions?
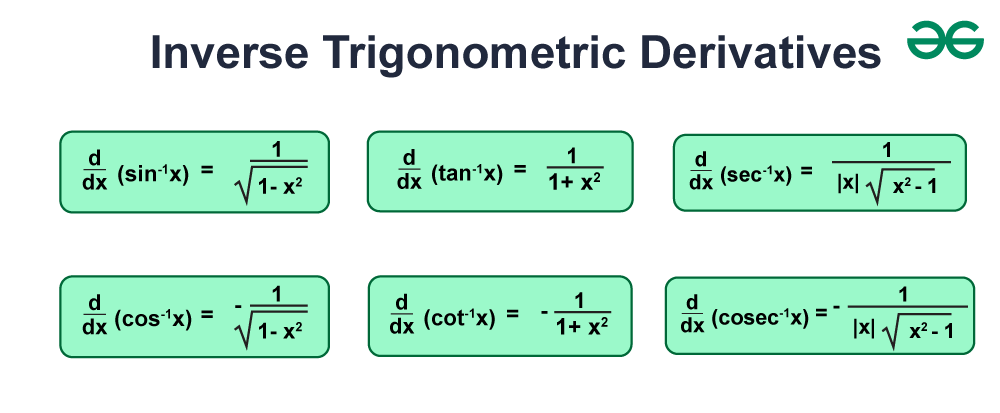
Inverse Trig Derivative are the derivative of inverse trigonometric functions. There are six trigonometric functions and there exists inverse for each of these trigonometric functions. These are sin-1x, cos-1x, tan-1x, cosec-1x, sec-1x, cot-1x. We can find the derivative of inverse trigonometric functions using the implicit differentiation method. Let’s learn first what are the derivatives of inverse trigonometric functions.
- Derivative of sin-1x is d(sin-1x)/dx = 1/√(1 – x2) for all x ϵ (-1, 1)
- Derivative of cos-1x is d(cos-1x)/dx = -1/√(1 – x2) for all x ϵ (-1, 1)
- Derivative of tan-1x is d(tan-1x)/dx = 1/(1 + x2) for all x ϵ R
- Derivative of cosec-1x is d(cosec-1x)/dx = -1/{|x|√(x2 – 1)} for all x ϵ R – [-1, 1]
- Derivative of sec-1x is d(sec-1x)/dx = 1/{|x|√(x2 – 1)} for all x ϵ R – [-1, 1]
- Derivative of cot-1x is d(cot-1x)/dx = -1/(1 + x2) for all x ϵ R
The image for the Inverse Trigonometric Derivative is attached below:
Now we have learnt what are the derivatives of all the six inverse trigonometric functions, we will now learn how to find the derivative of the six inverse trig functions.
Proof of Derivative of Inverse Trig Functions
We can differentiate the inverse trigonometric functions using the first principle and also by using implicit differentiation formula which also involves the use of chain rule. To find the derivative of inverse trigonometric functions using first principle is a lengthy process. In this article we learn how to differentiate inverse trigononetric functions using implicit differentiation. We can find the derivative (dy/dx) of inverse trig functions using following steps
Step 1: Assume the trigonometric functions in the form siny = x
Step 2: Find the derivative of above function using implicit differentiation
Step 3: Calculate dy/dx
Step 4: Replace the value of trigonometric function present in the step 3 using trigonometric identities.
Derivative of sin inverse x
Let us assume sin y = x
Differentiating both side with respect to x
⇒ cos y. dy/dx = 1
⇒ dy/dx = 1/cos y →(i)
Since we know that Sin2y + Cos2y = 1
⇒ Cos2y = 1 – sin2y
⇒ cosy = √(1 – sin2y) = √(1 – x2) as we have sin y = x
Putting this value of cos y in equation (i)
dy/dx = 1/√(1 – x2) where y = sin-1x
Derivative of cos inverse X
Let us assume cos y = x
Differentiating both side with respect to x
⇒ -sin y. dy/dx = 1
⇒ dy/dx = -1/sin y →(i)
Since we know that Sin2y + Cos2y = 1
⇒ sin2y = 1 – cos2y
⇒ sin y = √(1 – cos2y) = √(1 – x2) as we have cos y = x
Putting this value of sin y in equation (i)
dy/dx = -1/√(1 – x2) where y = cos-1x
Derivative of tan inverse X
Let us assume tan y = x
Differentiating both side with respect to x
⇒ sec2y. dy/dx = 1
⇒ dy/dx = 1/sec2y →(i)
Since we know that sec2y – tan2y = 1
⇒ sec2y = 1 + tan2y
⇒ sec2y = (1 + tan2y) = (1 + x2) as we have tan y = x
Putting this value of sec2y in equation (i)
dy/dx = 1/(1 + x2) where y = tan-1x
Derivative of cot inverse X
Let us assume cot y = x
Differentiating both side with respect to x
⇒ -cosec2 y. dy/dx = 1
⇒ dy/dx = -1/cosec2y →(i)
Since we know that csec2y – cot2y = 1
⇒ cosec2y = 1 + cot2y
⇒ cosec2y = (1 + cot2y) = (1 + x2) as we have cot y = x
Putting this value of cosec2y in equation (i)
dy/dx = -1/(1 + x2) where y = cot-1x
Derivative of sec inverse X
Let us assume sec y = x
Differentiating both side with respect to x
⇒ sec y.tan y.dy/dx = 1
⇒ dy/dx = 1/sec y.tan y →(i)
Since we know that sec2y – tan2y = 1
⇒ tan2y = sec2y – 1
⇒ tan y = √(sec2y – 1) = √(x2 – 1)as we have sec y = x
Putting this value of tan y in equation (i)
dy/dx = 1/{|x|√(x2 – 1)} where sec y = x and y = sec-1x
Derivative of cosec inverse X
Let us assume cosec y = x
Differentiating both side with respect to x
⇒ -cosec y.cot y.dy/dx = 1
⇒ dy/dx = -1/cosec y.cot y →(i)
Since we know that cosec2y – cot2y = 1
⇒ cot2y = cosec2y – 1
⇒ cot y = √(cosec2y – 1) = √(x2 – 1)as we have cosec y = x
Putting this value of tan y in equation (i)
dy/dx = -1/{|x|√(x2 – 1)} where cosec y = x and y = cosec-1x
Now we have learnt how to differentiate the Inverse Trigonometric Functions, hence we will look now the formulas for the derivative of the inverse trigonometric functions which can be used directly in the problems. Given below is the table of derivative of inverse trigonometric function formula.
|
| sin-1x | 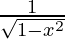 |
| cos-1x | 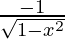 |
| tan-1x | 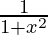 |
| cot-1x | 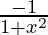 |
| sec-1x | 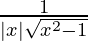 |
| cosec-1x | 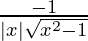 |
Read More,
Inverse Trig Derivative Examples
Example 1: Differentiate sin-1 (x)?
Solution:
Let, y = sin−1 (x)
Taking sine on both sides of equation gives,
sin y = sin(sin-1x)
By the property of inverse trigonometry we know, sin(sin-1x) = x
sin y = x
Now differentiating both sides wrt to x,
d/dx{sin y} = d/dx{x}
{cos y}.dy/dx = 1
dy/dx = 1/ {cos y}
We can simplify it more by using the below observation:
sin2y + cos2y = 1
x2 + cos2y = 1 {As sin y = x}
cos2y = 1-x2
cos y = √(1 – x2)
Substituting the value, we get
dy/dx = 1/{cos y}
⇒ dy/dx = 1/√(1 – x2)
Example 2: Differentiate cos-1 (x)?
Solution:
Let,
y = cos−1 (x)
Taking cosine on both sides of equation gives,
cos y = cos(cos-1x)
By the property of inverse trigonometry we know, cos(cos-1x) = x
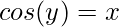
Now differentiating both sides wrt to x,
d/dx{cos y} = d/dx{x}
{-sin y}.dy/dx = 1
dy/dx = -1/sin y
We can simplify it more by using the below observation:
sin2y + cos2y = 1
sin2y + x2 = 1 {As cos y = x}
sin2y = 1-x2
sin y = √(1 – x2)
Substituting the value, we get
dy/dx = -1/{sin y}
⇒ dy/dx = -1/√(1 – x2)
Example 3: Differentiate tan-1 (x)?
Solution:
Let, y = tan−1 (x)
Taking tan on both sides of equation gives,
tan y = tan(tan-1x)
By the property of inverse trigonometry we know, tan(tan-1x) = x
tan y = x
Now differentiating both sides wrt to x,
d/dx{sin y} = d/dx{x}
sec2(x).dy/dx= 1
dy/dx = 1/sec2x
We can simplify it more by using the below observation:
sec2y – tan2y = 1
sec2y – x2 = 1
sec2y = 1 + x2
Substituting the value, we get
dy/dx = 1/sec2y
dy/dx = 1/(1 + x2)
Example 4: y = cos-1 (-2x2). Find dy/dx at x = 1/2?
Solution:
Method 1 (Using implicit differentiation)
Given, y = cos−1 (−2x2)
⇒ cos y = −2x2
Differentiating both sides wrt x
d/dx{cos y} = d/dx{-2x2}
{-sin y}.dy/dx = -4x
dy/dx = 4x/sin y
Simplifying
sin2y + cos2y = 1
sin2y + (-2x2)2 = 1 {As cos y = -2x2}
sin2y + 4x4 = 1
sin2y = 1 – 4x4
sin y = √(1 – 4x4)
Putting the obtained value we get,
dy/dx = 4x/√{1 – 4x4}
⇒ dy/dx = 4(1/2)/√{1 – 4(1/2)4}
⇒ dy/dx = 2/√{1 – 1/4}
⇒ dy/dx = 2/√{3/4}
⇒ dy/dx = 4/√3
Method 2 (Using chain rule as we know the differentiation of cos inverse x)
Given, y = cos−1 (−2x2)
Differentiating both sides wrt x

Example 5: Differentiate 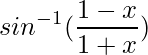
Solutions:
Let,
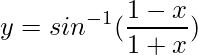
Differentiating both sides wrt x
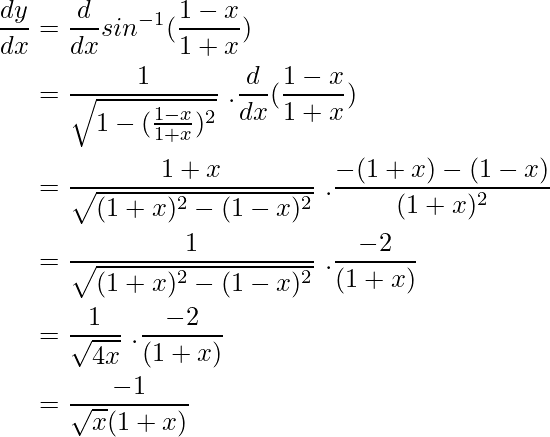
Inverse Trig Derivative Questions
Q1: Differentiate sin-1(3x – 4x3) for x ϵ -1/2 < x < 1/2
Q2: Differentiate cos-1(2x2 – 1) for 0 < x < 1
Q3: Differentiate tan-1(2x/1 – x2) for x ϵ (-1, 1)
Q4: Differentiate sin-1(2x/1 + x2) for x ϵ (-1, 1)
FAQs on Inverse Trig Derivative
1. What are Inverse Trigonometric Functions?
Inverse Trigonometric Function are the inverse of the six trigonometric functions sin, cos, tan, cosec, sec and cot. They are represented as if sin y = x then y = sin-1x
2. What is Inverse Trig Derivative?
Inverse Trig Derivative is the rate of change in the inverse trigonometric functions with respect to independent variable.
3. How to differentiate Inverse Trigonometric Functions?
We can find the derivative of inverse trigonometric by First Principle and by Implicit Differentiation Formula. The proof of the derivative of all the six inverse trigonometric functions are discussed in the article.
4. What is the Derivative of sin-1 x?
The derivative of sin-1x is d(sin-1x)/dx = 1/√(1 – x2) for all x ϵ (-1, 1)
5. What is the Derivative of cos-1x?
The derivative of cos-1x is d(cos-1x)/dx = -1/√(1 – x2) for all x ϵ (-1, 1)
6. What is the Derivative of tan-1x?
The derivative of tan-1x is d(tan-1x)/dx = 1/(1 + x2) for all x ϵ R
7. What is the Derivative of cosec-1x?
The derivative of cosec-1x is d(cosec-1x)/dx = -1/{|x|√(x2 – 1)} for all x ϵ R – [-1, 1]
8. What is the Derivative of sec-1x?
The derivative of sec-1x is d(sec-1x)/dx = 1/{|x|√(x2 – 1)} for all x ϵ R – [-1, 1]
9. What is the Derivative of cot-1x?
The derivative of cot-1x is d(cot-1x)/dx = -1/(1 + x2) for all x ϵ R
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...