Different Types of Clustering Algorithm
Last Updated :
22 Apr, 2023
The introduction to clustering is discussed in this article and is advised to be understood first.
The clustering Algorithms are of many types. The following overview will only list the most prominent examples of clustering algorithms, as there are possibly over 100 published clustering algorithms. Not all provide models for their clusters and can thus not easily be categorized.
Distribution-based methods:
It is a clustering model in which we will fit the data on the probability that how it may belong to the same distribution. The grouping done may be normal or gaussian. Gaussian distribution is more prominent where we have a fixed number of distributions and all the upcoming data is fitted into it such that the distribution of data may get maximized. This result in grouping is shown in the figure:
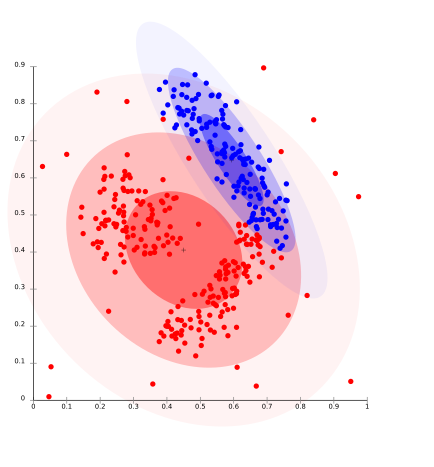
This model works well on synthetic data and diversely sized clusters. But this model may have problems if the constraints are not used to limit the model’s complexity. Furthermore, Distribution-based clustering produces clusters that assume concisely defined mathematical models underlying the data, a rather strong assumption for some data distributions.
For Ex- The expectation-maximization algorithm which uses multivariate normal distributions is one of the popular examples of this algorithm.
Centroid-based methods:
This is basically one of the iterative clustering algorithms in which the clusters are formed by the closeness of data points to the centroid of clusters. Here, the cluster center i.e. centroid is formed such that the distance of data points is minimum with the center. This problem is basically one of the NP-Hard problems and thus solutions are commonly approximated over a number of trials.
For Ex- K – means algorithm is one of the popular examples of this algorithm.
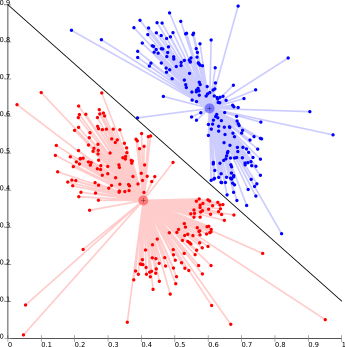
The biggest problem with this algorithm is that we need to specify K in advance. It also has problems in clustering density-based distributions.
Connectivity based methods :
The core idea of the connectivity-based model is similar to Centroid based model which is basically defining clusters on the basis of the closeness of data points. Here we work on a notion that the data points which are closer have similar behavior as compared to data points that are farther.
It is not a single partitioning of the data set, instead, it provides an extensive hierarchy of clusters that merge with each other at certain distances. Here the choice of distance function is subjective. These models are very easy to interpret but it lacks scalability.
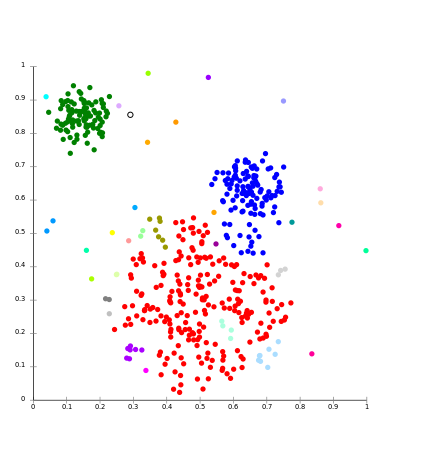
For Ex- hierarchical algorithm and its variants.
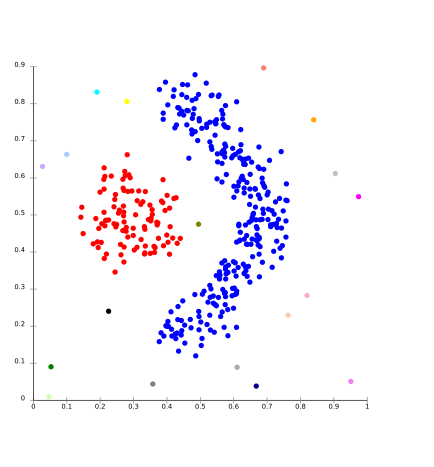
Density Models: In this clustering model, there will be searching of data space for areas of the varied density of data points in the data space. It isolates various density regions based on different densities present in the data space.
For Ex- DBSCAN and OPTICS.
Subspace clustering: Subspace clustering is an unsupervised learning problem that aims at grouping data points into multiple clusters so that data points at a single cluster lie approximately on a low-dimensional linear subspace. Subspace clustering is an extension of feature selection just as with feature selection subspace clustering requires a search method and evaluation criteria but in addition subspace clustering limits the scope of evaluation criteria. The subspace clustering algorithm localizes the search for relevant dimensions and allows them to find the cluster that exists in multiple overlapping subspaces. Subspace clustering was originally purposed to solve very specific computer vision problems having a union of subspace structures in the data but it gains increasing attention in the statistic and machine learning community. People use this tool in social networks, movie recommendations, and biological datasets. Subspace clustering raises the concern of data privacy as many such applications involve dealing with sensitive information. Data points are assumed to be incoherent as it only protects the differential privacy of any feature of a user rather than the entire profile user of the database.
There are two branches of subspace clustering based on their search strategy.
- Top-down algorithms: These algorithms start by finding an initial clustering in the full set of dimensions and then evaluate the subspace of each cluster. The idea is to identify the subspace that captures the most significant variation in the data points within a cluster. This approach is also known as projection-based clustering because it involves projecting the data onto different subspaces and clustering the resulting lower-dimensional data. Top-down algorithms are useful for discovering clusters that exhibit different patterns in different subspaces. Top-down algorithms find an initial clustering in the full set of dimensions and evaluate the subspace of each cluster.
- Bottom-up algorithms: These algorithms start by identifying dense regions in a low-dimensional space (often using a density-based clustering algorithm like DBSCAN) and then combine these regions to form clusters in the full-dimensional space. The idea is to find dense regions that are present in multiple subspaces and use them to infer the underlying cluster structure of the data. This approach is also known as subspace merging because it involves merging clusters that are identified in different subspaces. Bottom-up algorithms are useful for discovering clusters that exhibit similar patterns across different subspaces. The bottom-up approach finds dense region in low dimensional space then combine to form clusters.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...