Centripetal and Centrifugal Force
Last Updated :
22 Apr, 2024
Centripetal and Centrifugal Force – An object performing a circular motion is changing its velocity every second. That means a force acts on the particle which makes it move in a circular motion that changes at every instance. The forces acting on the object in circular motion are centripetal force and centrifugal force. These forces allow objects to move in a circular motion.
Let’s learn more about centripetal force and centrifugal force and their differences in this article.
What is Centripetal Force?
The force acting on the object which is moving in a curvilinear motion is called the Centripetal Force. It allows the object to maintain its curvilinear motion. We can define the centripetal force as,
“The force acting on an object that is in the curvilinear motion and the force is directed toward the centre of the curvature of the path of the object is called the Centripetal Force.”
The word centripetal means “centre seeking” or “toward the centre”. Thus, we can easily define the Centripetal Force as the force which acts toward the centre when an object is performing a curvilinear motion.
Calculating Centripetal Force
The magnitude of centripetal force is by the formula,
F = mv2/r
where,
m is the mass of the object
v is the velocity of the object
r is the radius of the object
Thus, it is clear from the above formula that Centripetal Force is directly proportional to the square of the velocity of the object slight increase in the velocity of the object increases the force drastically.
Unit of Centripetal Force
As centripetal force is itself a force it is measured in Netwon which is the SI unit of Force. Other units to measure the centripetal force are kgms-2, dyne, etc.
In the circular motion, the centripetal force is always directed towards the centre and it is always perpendicular to the tangent which gives the direction at any given point.
Examples of Centripetal Force in Daily Life
Centripetal force is responsible for the circular motion of the object. Various examples exhibiting Centripetal Force are discussed in the image below,
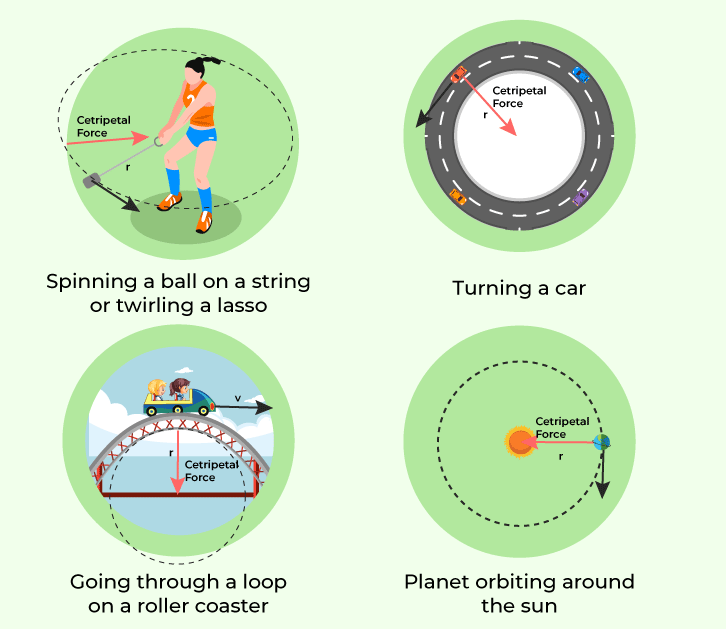
- When we tie a ball to the end of the string and rotate the string the tension experience in the string in the example of Centripetal Force.
- Frictional force required for the turning of wheel in the car is provided by the centripetal force.
- In a roller coaster the force provided to balance the normal force is the force provided by the centripetal force.
- Planets revolving around the sun also experience centripetal foce because of the gravitaional force.
What is Centrifugal Force?
Centrifugal Force force is also a force that acts when the object is in a circular motion. This force has the same magnitude as a centripetal force but is in the opposite direction of the centripetal force.
This is a kind of pseudo-force acting in the curvilinear motion which opposes the centripetal acceleration and acts as its reaction force. Centrifugal Force only works in the rotational frame of reference.
Calculating Centrifugal Force
The centripetal force is by the formula,
F = -mv2/r
where,
m is the mass of the object
v is the velocity of the object
r is the radius of the object
Here, the minus sign represents that the centrifugal force is oppositive in nature.
Unit of Centrifugal Force
Its unit is also Newton (N), this force does not exist when measurements are made in an inertial frame of reference, it only exists when the measurement is made with respect to the rotating frame of reference.
Examples of Centrifugal Force in Daily Life
Centrifugal Force acts only in the rotating frame of reference. Various examples of objects under the influence of centrifugal force are:
Changes according to image
- Weight of an object at the poles and on the equator
- A bike making a turn.
- Vehicle driving around a curve
- Equatorial railway
Centrifuge is a device to separate a mixture of fluids which works on the principle of Centrifgation.
Centripetal Force vs Centrifugal Force
Both of these forces are essential for circular motion. While centripetal force is a real force by nature and acts in the inertial frame of reference, the centrifugal force is a pseudo force and acts in an internal frame,
for example – The rotating frame of reference. Both of these forces are equal in magnitude and in opposite directions. Intuitively, the centrifugal force has a tendency to keep the object travelling in a straight line and oppose the turn, on the other hand, the centripetal force causes the object to move in a circular motion. Let’s take a look at the differences in tabular form,
|
Centripetal Force
|
Centrifugal Force
|
| It is known as a real force that exists and is externally applied. Forces like gravitational force, normal force, etc. |
It is known as a fictitious or pseudo-force. |
| It is the force exerted on the object in a circular motion. The force is acted towards the centre of the circle. |
It is the force exerted on the object in a circular motion. The force is acted away from the centre of the circle. |
| The centripetal force acts in inertial both inertial and non-inertial frames. |
The centrifugal force acts in a non-inertial frame. (Rotating frames) |
| Example: A satellite orbiting around the planet is an example where centripetal force is used. |
Man sitting inside the car leans outwards while the car moves inwards is an example of centrifugal force. |
Read More,
Solved Examples on Centripetal Force and Centrifugal Force
Example 1: Find the centripetal acceleration on an object performing circular motion with a radius of 20m. The velocity of the object is 100m/s.
Solution:
Centripetal Acceleration is given by,
a = v2/r
Given:
v = 100m/s
r = 20m
Plugging the values in the equation,
a = v2/r
a = (100)2/(20)
a = 10000/20
a = 500 m/s2
Example 2: An object(m = 8Kg) is performing circular motion with a radius of 2m. If the velocity of the object is 10 m/s, find the centripetal force acting on the object.
Answer:
The centripetal acceleration is given by,
F = mv2/r
Given:
m = 8 kg
v = 10 m/s
r = 2 m
Plugging the values in the equation,
F = mv2/r
F = (8)(10)2/(2)
= 400 N
Example 3: An object(m = 1Kg) is performing circular motion with a radius of 4m. If the centripetal force acting on the object is 100N, find the velocity of the object.
Solution:
Force Acting on the object is given by,
F = ma
100 = (1)(a)
a = 100 m/s2
Acceleration of the object is given by,
a = v2/r
100 = v2/4
400 = v2
v = 20 m/s
Centripetal Force and Centrifugal Force – FAQs
What is centripetal force?
The force acting on the object which is performing curvilinear motion helps the object to keep its position while performing the curvilinear motion is called the centripetal force. This force is directed towards the centre of curvature.
What are examples of centripetal force?
Motion of the Earth around the sun is considered as curvilinear motion and the force which makes the Earth move in this motion is called the centripetal force.
Similarly, motion of Moon around the Earth is caused by centripetal force.
How does a Centrifuge work?
The centrifuge is a device which is used to separate two substance using centrifugal force. For example, we can separate plasma and blood cells from the blood using a centrifuge.
Which force acts in the washing machine?
In a rotating washing machine, both centrifugal force and centripetal force work simultaneously.
What is difference between centrifugal force and centripetal force?
The basic difference between the centrifugal force and centripetal force is that centripetal force always acts towards the centre of curvature whereas centrifugal force acts away from the centre of the curvature. Also, the centripetal force is observed in the inertial frame of reference, while centrifugal force is observed in the non-inertial or rotating frame of reference.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...