Difference between Tree edge and Back edge in graph

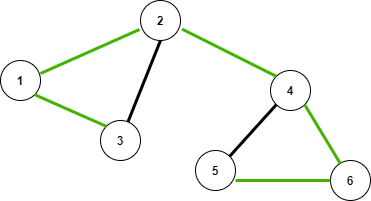
Tree Edge: It is an edge that is present in the tree obtained after performing DFS on the graph. All the Green edges are tree edges as shown in the below image. 

Back Edge: It is an edge (u, v) such that v is an ancestor of node u but not part of the DFS Traversal of the tree. Edge from 5 to 4 is a back edge. The presence of a back edge indicates a cycle in a directed graph.

Consider an undirected graph is given below, the DFS of the below graph is 3 1 2 4 6 5. In the below diagram, if the DFS is applied to this graph, a tree is obtained which is connected using green edges.

Tabular between the back Edge and tree Edge:

S.N.	Tree Edge	Back Edge
1	It connects the node to its descendants.	It connects the node to its ancestors.
2	It is the path traversed during DFS.	It is the path not visited during DFS.
3	They can form bridges.	They can never form bridges.
4	If it is disconnected, the number of connected components may increase.	Even if it is disconnected, the number of connected components remains the same.
5	It never creates a cycle.	It can create a cycle.