Difference between Stack and Tree
Last Updated :
14 Dec, 2020
Stack: A Stack is a linear data structure in which elements can be inserted and deleted only from one side of the list, called the top. Insertion is called push operation and deletion is called pop operation in case of the stack. The order of insertion and deletion may be LIFO(Last In First Out) i.e., the element inserted latest to the stack will also be inserted first. In stack, the track of the last element present in the list is tracked with a pointer called top. Below is the diagrammatic representation of the same:
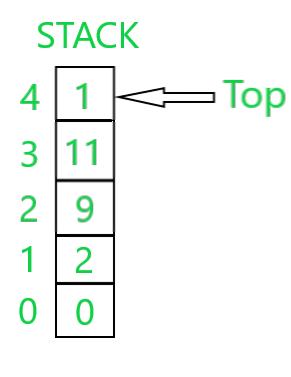
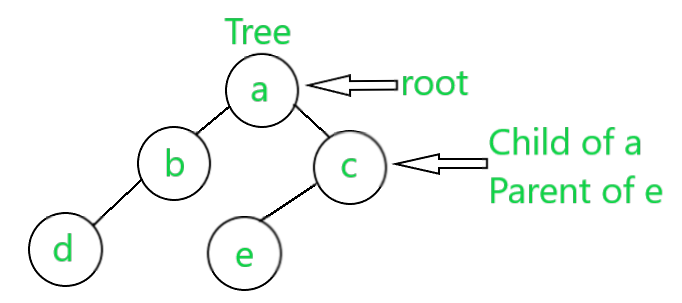
Tree: A Tree tree is a finite set of one or more nodes such that:
- There is a specially designated node called root.
- The remaining nodes are partitioned into N>=0 disjoint sets T1, T2, T3, …, TN, where T1, T2, T3, …, TN is called the subtree of the root.
Each node has a specific parent and may or may not have a child node. Each node contains a value and references to the children. It’s a kind of graph data structure but does not have cycles and is fully connected. The concept of a tree is represented in the below diagram:
Below is the tabular difference between the Stack and Tree:
| S No. |
Parameter
|
Stack
|
Tree
|
| 1 |
Basic Nature |
Linear Data Structure |
Non-Linear Data Structure |
| 2 |
Base Notion |
Top of the stack |
The root of the Tree |
| 3 |
Successor |
Element pushed before the reference element |
The notion of child and parent exists |
| 4 |
Order of Insertion |
Elements inserted on the TOP of the stack |
Depends on the type of tree. |
| 5 |
Order of Deletion |
Elements deleted from the TOP of the stack |
Depends on the type of tree. |
| 6 |
Insertion Complexity |
O(1) |
Depends on the type for example AVL- O(log2N). |
| 7 |
Deletion Complexity |
O(1) |
Depends on the type for example AVL- O(log2N). |
| 8 |
Searching |
O(1) |
Depends on the type for example AVL- O(log2N). |
| 9 |
Finding Min |
O(N) |
Depends on the type for example Min Heap- O(log2N). |
| 10 |
Finding Max |
O(N) |
Depends on the type for example Min Heap- O(log2N). |
| 11 |
IsEmpty |
O(1) |
Mostly O(1) |
| 12 |
Implementation |
Using arrays and linked list |
Can be implemented using array and user-defined type of nodes |
| 13 |
Types |
No types exist |
Many types like Binary Tree, AVL Tree, nary Tree, etc. |
| 14 |
Applications |
Expression evaluation, Backtracking, Memory management, etc. |
Fast search, insert, delete, etc. |
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...