Difference between Gradient descent and Normal equation

In regression models, our objective is to discover a model that can make predictions that closely resemble the actual target values. Basically, we try to find the parameters of the model which support our objective of the best model. The general behind finding this parameter is that we calculate the error between our actual value and predicted value and based on the error we manipulate the parameter which gives the lowest error.    

For models like Linear Regression, we can use two types of techniques to find the parameter: Normal Equation and Gradient descent. 

Gradient Descent

Gradient Descent is an iterative optimization algorithm that is used to find the values of parameters of a function that minimizes a cost function. It is one of the most used optimization techniques in machine learning projects for updating the parameters of a model in order to minimize a cost function. Parameters refer to coefficients in Linear Regression and weights in neural networks. 

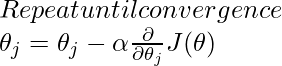
Gradient descent can also converge even if the learning rate is kept fixed. 

Python Implementation of Gradient Descent 

We can apply gradient descent to our input feature using the numpy library. However, to apply gradient we have to choose some hyperparameters which can be learned itself by the model.  

Python3

import numpy as np

def gradient_descent(X, y):
    # Decide learning rate value
    learning_rate = 0.01
    # Decide number of iterations
    num_iterations = 100
    # Get the number of rows and columns in the dataset
    num_samples, num_features = X.shape
    # Initialize random weights
    weights = np.random.randn(num_features)

    for iteration in range(num_iterations):
        permutation = np.random.permutation(num_samples)
        X = X[permutation]
        y = y[permutation]

        gradients = np.zeros(num_features)
        predictions = np.dot(X, weights)
        error = predictions - y
        gradients += 2 * np.dot(X.T, error) / num_samples
        # Update weights
        weights -= learning_rate * gradients

    return weights

X = np.array([[1, 2], [3, 4], [5, 6]])
y = np.array([3, 7, 11])

weights = gradient_descent(X, y)

# To make prediction on dataset
X_test = np.array([[3, 4], [5, 4], [7, 9]])
predictions = np.dot(X_test, weights)
print(predictions)

Output:

[ 6.90093216 10.1567656  15.93407653]

Normal Equation

Normal Equation is an analytical approach used for optimization. It is an alternative for Gradient descent. Normal equation performs minimization without iteration. Normal equations directly compute the parameters of the model that minimizes the Sum of the squared difference between the actual term and the predicted term of the dataset without needing to choose any hyperparameters like learning rate or the number of iterations. 

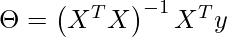
Where 
X = input feature value 
y = output value 
If the term 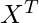X is non-invertible or singular then we can use regularization. 

Python implementation of Normal Equation in Gradient Descent 

We can use the numpy library to apply linear algebra functions on datasets to get the parameter of the linear regression Model. Also, we will add 1 to the beginning of each row of the matrix to get the bias parameter of the model. 

Python3

import numpy as np

# Input features
X = np.array([[1, 1], [1, 2], [1, 3], [1, 4]])

# Target values
y = np.array([[2], [3], [4], [5]])

# Transpose of X
X_transpose = X.T

# Compute X^T * X
X_transpose_X = np.dot(X_transpose, X)

# Compute X^T * y
X_transpose_y = np.dot(X_transpose, y)

# Add the identity matrix to X_transpose_X
X_with_intercept = X_transpose_X + np.eye(X_transpose_X.shape[0])

# Solve the normal equation
theta = np.linalg.solve(X_with_intercept, X_transpose_y)
# Input features for testing
X_test = np.array([[1], [4]])
X_test_with_intercept = np.c_[np.ones((X_test.shape[0], 1)), X_test]

predictions = np.dot(X_test_with_intercept, theta)
print(predictions)

Output:

[[1.70909091][4.98181818]]

Difference between Gradient Descent and the Normal Equation. 

Gradient Descent	Normal Equation
In gradient descent, we need to choose the learning rate, Number of iterations, and another hyperparameter.	In the normal equation, there is no need to choose the learning rate.
It is an iterative algorithm.	It is an analytical approach.
Gradient descent works well with large number of features.	Normal equation works well with small number of features.
Feature scaling can be used.	No need for feature scaling.
No need to handle non-invertibility cases.	If (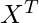X) is non-invertible, regularization can be used to handle this.
Time complexity of the gradient descent algorithm depends upon number of iterations and data size	The time complexity of the normal equation depends upon on the matrix inversion operation of the input feature