Difference between EMF and Potential Difference
Last Updated :
10 Dec, 2021
While working with batteries and cells in real life, we experience two different potential differences between the terminals of the battery. These potential differences are due to the non-ideal nature of the battery which increases the resistance inside the battery. The potentiometer is used to measure such differences. These different values are called e.m.f and the potential difference of a cell. To understand why this phenomenon occurs, we need to look at the resistance offered by the circuit and the battery. Let’s look at these concepts in detail.
Electromotive Force (E.M.F) of a Cell
The energy delivered to the unit charge by a cell is known as the electromotive force EMF. The batteries are available in a variety of forms and sizes. There are numerous distinct types of generators that are powered by various sources. All these devices irrespective of what their energy sources are, create potential differences across their terminals and can supply current if resistance is connected to them. It is known that potential difference creates an electric field that causes charges to move and that in turn creates current. Thus, this potential difference is sometimes also referred to as electromotive force (emf).
Contrary to its name, emf is not a force at all. It is a potential difference. If stated in precise terms,
E.M.F is a potential difference which is created when no current is flowing in the system.
Its unit is considered to be all Volts(V). Even though EMF is directly related to the potential difference produced by the voltage source, but it still differs from the actual potential difference that is reflected on the terminals of the battery. The terminal voltage around the battery is usually less than the e.m.f of the battery.
Potential Difference of a Cell
The voltage output of a battery is measured through its terminals and that is why it is termed as terminal voltage. In the figure given below, a battery and its internal resistance are shown. The battery is connected to another external resistance in series which is denoted by Rload. The net voltage developed across the terminals of the battery is given by the equation written below,
V = emf – Ir

Here, “I” is the current that is flowing in the circuit, and “r” is the internal resistance.
“I” is considered to be positive if the direction of its flow is from the negative to the positive terminal of the battery. The equation shows that the larger the current, the lower is the terminal voltage of the battery. It can also be concluded that the smaller the internal resistance, the greater is the terminal voltage. When the load resistor is taken into account, the current calculation becomes a little bit different.
The equivalent resistance of the circuit becomes,
R = r + Rload
The current is given by Ohm’s law,
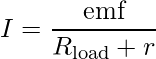
Difference between EMF and Potential Difference
Electromotive Force (E.M.F)
| Potential Difference
|
| The difference in the potential of two electrodes of a battery. | Difference of potential between any two points on the circuit. |
| E.M.F is always greater than the potential difference between any points in the circuit. | This is always less than the E.M.F |
| Formula: E = I(R + r) | Formula: V = IR |
| This is caused by the electric, gravitational and magnetic fields. | This difference is only produced by the electric field. |
| The electromotive force is the amount of energy given to each coulomb of charge. | The potential difference is the amount of energy utilized by one coulomb of charge. |
| The electromotive force is independent of the circuit’s internal resistance. | The potential difference is proportional to the circuit’s resistance. |
| The electromotive force is responsible for transferring energy across the circuit. | The potential difference between any two places on the circuit is a measure of energy. |
| When the circuit is unchanged, the magnitude of the electromotive force is always larger than the potential difference. | When the circuit is completely charged, the size of the potential difference is equal to the circuit’s emf. |
| The electromotive force is measured using an emf meter. | The potential difference is measured with a voltmeter. |
Sample Problems
Problem 1: Find the current that will flow inside the battery of 2 Volts and 0.02 ohms internal resistances in case its terminals are connected with each other.
Solution:
The current in that case will be given by simple application of ohm’s law.
V = 2V
r = 0.02 ohms.
V = IR
Plugging the values in the equation,
I = V/R
I = 2/0.02
= 100 A
Problem 2: Find the current that will flow inside the battery of 10 Volts and 5 ohms internal resistances in case its terminals are connected with each other.
Solution:
The current in that case will be given by simple application of ohm’s law.
V = 10 V
R = 5 ohms.
V = IR
Plugging the values in the equation,
I = V/R
I = 10/5
= 2 A
Problem 3: Find the current that will flow inside the battery of 10 Volts and 10 ohms internal resistances in case its terminals are connected with each other. Find the terminal voltage of the battery.
Solution:
The current in that case will be given by simple application of ohm’s law.
V = 10 V
R= 10 ohms.
V = IR
Plugging the values in the equation,
I = V/R
I = 10/10
= 1 A
The terminal voltage of the battery is given by,
V = emf – Ir
Given , emf = 10 V, I = 1A and r = 10
V = emf – Ir
= 10 – (1)(10)
= 0 V
Problem 4: Find the current that will flow inside the battery of 10 Volts and 5 ohms internal resistances and 5 ohms load resistance in series. Find the terminal voltage of the battery.
Solution:
The current in that case will be given by simple application of ohm’s law.
I = 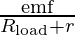
emf = 10 V
Rload= 5 ohms.
r = 5
Plugging the values in the equation,
I = 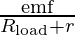
I = 10 / (5 + 5)
= 1 A
The terminal voltage of the battery is given by,
V = emf – Ir
Given , emf = 10 V, I = 1 A and r = 5
V = emf – Ir
= 10 – (1)(5)
= 10 – 5
= 5 V
Problem 5: Find the current that will flow inside the battery of 10 Volts and 2 ohms internal resistances and 3 ohms load resistance in series. Find the terminal voltage of the battery.
Solution:
The current in that case will be given by simple application of ohm’s law.
I = 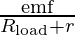
emf = 10 V
Rload= 3 ohms.
r = 2
plugging the values in the equation,
I = 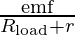
⇒ I = 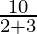
⇒ I = 2 A
The terminal voltage of the battery is given by,
V = emf – Ir
Given , emf = 10 V, I =2 A and r = 2
V = emf – Ir
= 10 – (2)(2)
= 10 – 6
= 4V
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...