Difference between Deterministic and Non-deterministic Algorithms

In deterministic algorithm, for a given particular input, the computer will always produce the same output going through the same states but in case of non-deterministic algorithm, for the same input, the compiler may produce different output in different runs. In fact non-deterministic algorithms can’t solve the problem in polynomial time and can’t determine what is the next step. The non-deterministic algorithms can show different behaviors for the same input on different execution and there is a degree of randomness to it.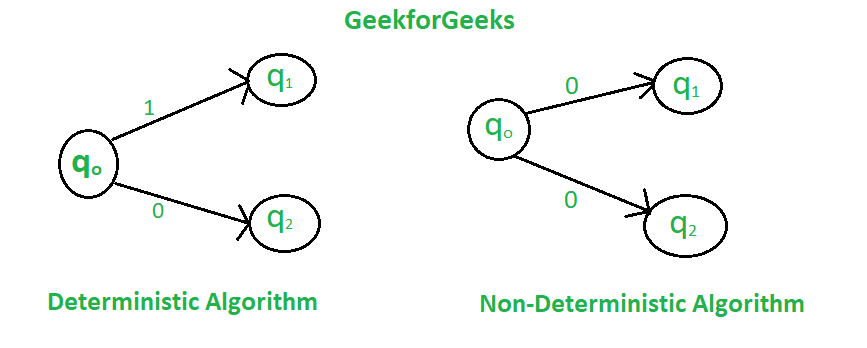

To implement a non-deterministic algorithm, we have a couple of languages like Prolog but these don’t have standard programming language operators and these operators are not a part of any standard programming languages.

Some of the terms related to the non-deterministic algorithm are defined below:

• choice(X) : chooses any value randomly from the set X.
• failure() : denotes the unsuccessful solution.
• success() : Solution is successful and current thread terminates.

Example :

Problem Statement : Search an element x on A[1:n] where n>=1, on successful search return j if a[j] is equals to x otherwise return 0.

Non-deterministic Algorithm for this problem :

1.j= choice(a, n)
2.if(A[j]==x) then
    {
       write(j);
       success();
    }
3.write(0); failure();

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

vivekkothari

Check out this Author's contributed articles.