Difference between Convolution VS Correlation

Correlation is a mathematical technique to see how close two things are related. In image processing terms, it is used to compute the response of a mask on an image. A mask is applied on a matrix from left to right. Mask slides over the matrix from left to right by one unit every time. Once the mask reaches the rightmost end, the mask is slid downward by one unit and again starts from left to right side. The computed output is assigned to the central pixel, while neighbourhood pixels are also get used in the computation. The mask or the matrix can be 1-D or 2-D. Generally, the mask’s dimension is taken as an odd number, so that the central pixel can easily be found.

Illustration:

Image, I = [100, 120, 100, 150, 160]Indexes of the image are 0, 1, 2, 3 and 4.

Mask, H = [1/3, 1/3, 1/3]Indexes of the mask are -1, 0 and 1.

Apply correlation between image and mask at index=2 in the image.

J(2) = I(1) . H(-1) + I(2) . H(0) + I(3) . H(1)Indexes are represented in the parentheses.

J(2) = 120 x 1/3 + 100 x 1/3 + 150 x 1/3

J(2) = 370/3

In general, J = I . H

Correlation is denoted by (.)

The formula of 1D correlation: 

• 

The formula of 2D correlation: 

• 

Note:

• The size of the resultant image depends on padding.
• If padding is allowed, size of resultant image = size of the original image (input)
• If padding is not allowed, size of resultant image < size of the input image.

A convolution is also a mathematical tool that is used to combine two things in order to produce the result. In image processing, convolution is a process by which we transform an input image by applying a kernel over it in a pixel-wise fashion. When the convolution mask operates on a particular pixel, then it performs the action by considering that pixel and its neighbouring pixels and the result is returned to that one particular pixel. Thus, we conclude that convolution in image processing is the mask operator. 

How to perform convolution

1. Flip the mask and do correlation.
2. The 1D mask is flipped horizontally, as there is a single row.
3. The 2D mask is flipped vertically and horizontally.
4. Mask is slid over the image matrix from the left to the right direction.
5. When the mask hovers on the image, corresponding elements of mask and image are multiplied and the products are added.
6. This process repeats for all the pixels of the image.

There are two types of operators in image processing. 

• Point operator: While operating on a particular pixel, it takes only one pixel as input that is itself.  For example Brightness increasing operation. We increase each pixel’s intensity by the same value to increase the brightness of the image.
• Mask operator: While performing an action on a particular pixel it takes the particular pixel and its neighbouring pixels as the input. Convolution operation.

Illustration:

Image, I = [100, 120, 100, 150, 160]

Indexes of the image are 0, 1, 2, 3 and 4.

Mask used for correlation, H = [1/3, 1/3, 1/3]

Indexes of the mask are -1, 0 and 1.

We are using same mask not the flipped one, hence we shall use the indexes properly.

Apply convolution between image and mask at index=1 in the image.

J(2) = I(0) . H(1) + I(1) . H(0) + I(2) . H(-1)Indexes are represented in the parentheses.

J = I * H

Convolution is denoted by (*).

Size of resultant image follows same as in case of correlation.

The formula of 1D convolution:

• 

The formula of 2D convolution: 

• 

Note: Convolution and correlation give the same response if the mask is symmetric. Both correlation and convolution look similar in nature. But we use convolution extensively in image processing because of its following properties.

Properties of convolution

• Convolution is associative in nature, but not the correlation. i.e. 
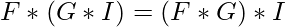
• Convolution is commutative in nature. i.e. 
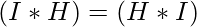
• Convolution follows linearity. i.e. 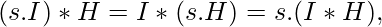 where s is any constant and multiplied to the mask or the image.
• Convolution follows separability if the mask is separable. i.e. If

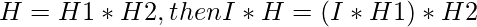
 Advantage of separability

If the kernel is separable then it can save computational cost.

Step 1: Matrix initialisation is done in one line in Matlab, 
order of matrix does not matter.

K = [1, 2, 3; 2, 4, 5];

Step 2: MatLab inbuilt method is used to create matrix of ones:

 H = ones(3,3).*1/9;

Step 3: We have used (.) before *, cause (.) means we are multiplying all elements of (3, 3) matrix by 1/9.

Initialise the linear mask of order 1 by 3:

 H1=ones(1,3).*1/3;

Initialise transpose mask, which is separated from the main mask:

H2=H1'

Step 4: Convolution between matrix K and mask H is applied using Matlab inbuilt function “conv2”

KH = conv2(K, H, 'same');

Step 5: Convolution between matrix K and mask H1: 

KH1 = conv2(K, H1, 'same');

Step 6: Convolution between result matrix KH1 and mask H2: 

KH2 = conv2(KH1, H2, 'same');

Example:

Matlab

% MATLAB Code for separable mask
% D convolution
% Define the matrix.
 K=[9 18 9 27 36;
    81 9 45 54 9;
    36 18 63 72 9];

% Define the averaging mask.
  H = ones(3,3).*1/9;

% Separate the mask.
 H1 = ones(1,3).*1/3;

% Transpose of separated mask.
 H2 = H1';

% Perform the same convolution.
  KH = conv2(K,H,'same')
  KH1 = conv2(K,H1,'same')
  KH2 = conv2(KH1,H2,'same')

Output: 

Code explanation: 

• First, we define the matrix image.
• After matrix creation, we define the main averaging mask, named H.
• Separable masks H1 and H2 are defined.
• The second mask is the transpose of mask1.
• The convolution between matrix K and mask H is calculated in the KH variable.
• The convolution between matrix K and mask H1 is stored in the KH1 variable.
• KH2 = conv2(KH1, H2, ‘same’); This line applies the convolution between result matrix KH1 and masks H2.
  This result is the same as KH.