Difference between Context Free Grammar and Regular Grammar

Noam Chomsky has divided grammar into four types :

Type	Name
0	Unrestricted Grammar
1	Context Sensitive Grammar
2	Context Free Grammar
3	Regular Grammar

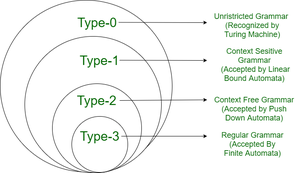
Chomsky Hierarchy

1. Context Free Grammar :

• Language generated by Context Free Grammar is accepted by Pushdown Automata
• It is a subset of Type 0 and Type 1 grammar and a superset of Type 3 grammar.
• Also called phase structured grammar.
• Different context-free grammars can generate the same context-free language.
• Classification of Context Free Grammar is done on the basis of the number of parse trees.
• Only one parse tree->Unambiguous.
• More than one parse tree->Ambiguous.

Productions are in the form –

A->B;
A∈N i.e A is a non-terminal.
B∈V*(Any string).

Example –

S –> AB
A –> a
B –> b

2. Regular Grammar :

• It is accepted by Finite State Automata.
• It is a subset of Type 0 ,Type 1 and Type 2 grammar.
• The language it generates is called Regular Language.
• Regular languages are closed under operations like Union, Intersection, Complement etc.
• They are the most restricted form of grammar.

Productions are in the form –

V –> VT / T (left-linear grammar)
  (or)
V –> TV /T (right-linear grammar)

Example –

1. S –> ab. 
2. S -> aS | bS | ∊ 

Difference Between Context Free Grammar and Regular Grammar:

Parameter	Context Free Grammar	Regular Grammar
Type	Type-2	Type-3
Recognizer	Push-down automata.	Finite State Automata
Rules	Productions are of the form: A->B;  A∈N(Non-Terminal)  B∈V*(Any string)	Productions are of the form: V –> VT / T (left-linear grammar) (or) V –> TV /T (right-linear grammar)
Restriction	Less than Regular Grammar	More than any other grammar
Right-hand Side	The right-hand side of production has no restrictions.	The right-hand side of production should be either left linear or right linear.
Set Property	Super Set of Regular Grammar	Subset of Context Free Grammar
Intersection	Intersection of two CFL need not be a CFL	Intersection of two RG is a RG.
Complement	They are not closed under complement	Closed under complement
Range	The range of languages that come under CFG is wide.	The range of languages that come under RG is less than CFG.
Examples	S –> AB;A –> a;B –> b	S -> aS | bS | ∊