Dial’s Algorithm (Optimized Dijkstra for small range weights)
Last Updated :
23 Jun, 2023
Dijkstra’s shortest path algorithm runs in O(Elog V) time when implemented with adjacency list representation (See C implementation and STL based C++ implementations for details).
Input : Source = 0, Maximum Weight W = 14
Output :
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
Consider the below Graph:

The shortest path from source 0
We have learned about how to find the shortest path from a given source vertex to all other vertex using Dijkstra’s shortest path algorithm with the Time Complexity of O(E log V) in this article.
Can we optimize Dijkstra’s shortest path algorithm to work better than O(E log V) if the maximum weight is small (or the range of edge weights is small)?
For example, in the above diagram, the maximum weight is 14. Many times the range of weights on edges is in a small range (i.e. all edge weights can be mapped to 0, 1, 2.. w where w is a small number). In that case, Dijkstra’s algorithm can be modified by using different data structures, and buckets, which is called dial implementation of Dijkstra’s algorithm. time complexity is O(E + WV) where W is the maximum weight on any edge of the graph, so we can see that, if W is small then this implementation runs much faster than the traditional algorithm.
The following are important observations.
- The maximum distance between any two nodes can be at max w(V – 1) (w is maximum edge weight and we can have at max V-1 edges between two vertices).
- In the Dijkstra algorithm, distances are finalized in non-decreasing, i.e., the distance of the closer (to given source) vertices is finalized before the distant vertices.
Algorithm
Below is the complete algorithm:
- Maintains some buckets, numbered 0, 1, 2,…,wV.
- Bucket k contains all temporarily labeled nodes with a distance equal to k.
- Nodes in each bucket are represented by a list of vertices.
- Buckets 0, 1, 2,..wV are checked sequentially until the first non-empty bucket is found. Each node contained in the first non-empty bucket has the minimum distance label by definition.
- One by one, these nodes with minimum distance labels are permanently labeled and deleted from the bucket during the scanning process.
- Thus operations involving vertex include:
- Checking if a bucket is empty
- Adding a vertex to a bucket
- Deleting a vertex from a bucket.
- The position of a temporarily labeled vertex in the buckets is updated accordingly when the distance label of a vertex changes.
- The process is repeated until all vertices are permanently labeled (or the distances of all vertices are finalized).
Implementation
Since the maximum distance can be w(V – 1), we create wV buckets (more for simplicity of code) for implementation of the algorithm which can be large if w is big.
C++
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f
class Graph
{
int V;
list< pair<int, int> > *adj;
public:
Graph(int V);
void addEdge(int u, int v, int w);
void shortestPath(int s, int W);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list< pair<int, int> >[V];
}
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(make_pair(v, w));
adj[v].push_back(make_pair(u, w));
}
void Graph::shortestPath(int src, int W)
{
vector<pair<int, list<int>::iterator> > dist(V);
for (int i = 0; i < V; i++)
dist[i].first = INF;
list<int> B[W * V + 1];
B[0].push_back(src);
dist[src].first = 0;
int idx = 0;
while (1)
{
while (B[idx].size() == 0 && idx < W*V)
idx++;
if (idx == W * V)
break;
int u = B[idx].front();
B[idx].pop_front();
for (auto i = adj[u].begin(); i != adj[u].end(); ++i)
{
int v = (*i).first;
int weight = (*i).second;
int du = dist[u].first;
int dv = dist[v].first;
if (dv > du + weight)
{
if (dv != INF)
B[dv].erase(dist[v].second);
dist[v].first = du + weight;
dv = dist[v].first;
B[dv].push_front(v);
dist[v].second = B[dv].begin();
}
}
}
printf("Vertex Distance from Source\n");
for (int i = 0; i < V; ++i)
printf("%d %d\n", i, dist[i].first);
}
int main()
{
int V = 9;
Graph g(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.shortestPath(0, 14);
return 0;
}
|
Python3
from typing import List, Tuple
INF = 0x3f3f3f3f
class Graph:
def __init__(self, V: int):
self.V = V
self.adj = [[] for _ in range(V)]
def addEdge(self, u: int, v: int, w: int):
self.adj[u].append((v, w))
self.adj[v].append((u, w))
def shortestPath(self, src: int, W: int):
dist = [[INF, None] for _ in range(self.V)]
dist[src][0] = 0
B = [[] for _ in range(W * self.V + 1)]
B[0].append(src)
idx = 0
while True:
while len(B[idx]) == 0 and idx < W * self.V:
idx += 1
if idx == W * self.V:
break
u = B[idx][0]
B[idx].pop(0)
for v, weight in self.adj[u]:
du = dist[u][0]
dv = dist[v][0]
if dv > du + weight:
if dv != INF:
B[dv].remove(v)
dist[v][0] = du + weight
dv = dist[v][0]
B[dv].append(v)
dist[v][1] = len(B[dv]) - 1
print("Vertex Distance from Source")
for i in range(self.V):
print(f"{i} {dist[i][0]}")
def main():
V = 9
W = 14
g = Graph(V)
g.addEdge(0, 1, 4)
g.addEdge(0, 7, 8)
g.addEdge(1, 2, 8)
g.addEdge(1, 7, 11)
g.addEdge(2, 3, 7)
g.addEdge(2, 8, 2)
g.addEdge(2, 5, 4)
g.addEdge(3, 4, 9)
g.addEdge(3, 5, 14)
g.addEdge(4, 5, 10)
g.addEdge(5, 6, 2)
g.addEdge(6, 7, 1)
g.addEdge(6, 8, 6)
g.addEdge(7, 8, 7)
g.shortestPath(0, W)
if __name__ == "__main__":
main()
|
C#
using System;
using System.Collections.Generic;
public class Graph
{
static readonly int INF = Int32.MaxValue;
private int V;
private List<Tuple<int, int> >[] adj;
public Graph(int v)
{
this.V = v;
this.adj = new List<Tuple<int, int> >[ v ];
for (int i = 0; i < v; i++)
this.adj[i] = new List<Tuple<int, int> >();
}
public void AddEdge(int u, int v, int w)
{
adj[u].Add(Tuple.Create(v, w));
adj[v].Add(Tuple.Create(u, w));
}
public void shortestPath(int src, int W)
{
int[] dist = new int[V];
for (int i = 0; i < V; i++)
dist[i] = INF;
List<int>[] B = new List<int>[ W * V + 1 ];
for (int i = 0; i < W * V + 1; i++)
B[i] = new List<int>();
B[0].Add(src);
dist[src] = 0;
int idx = 0;
while (true) {
while (B[idx].Count == 0 && idx < W * V)
idx++;
if (idx == W * V)
break;
int u = B[idx][0];
B[idx].Remove(u);
foreach(Tuple<int, int> i in adj[u])
{
int v = i.Item1;
int weight = i.Item2;
int du = dist[u];
int dv = dist[v];
if (dv > du + weight) {
dist[v] = du + weight;
dv = dist[v];
B[dv].Insert(0, v);
}
}
}
Console.WriteLine("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
Console.WriteLine("{0} {1}", i, dist[i]);
}
}
class GFG {
static void Main(string[] args)
{
int V = 9;
Graph g = new Graph(V);
g.AddEdge(0, 1, 4);
g.AddEdge(0, 7, 8);
g.AddEdge(1, 2, 8);
g.AddEdge(1, 7, 11);
g.AddEdge(2, 3, 7);
g.AddEdge(2, 8, 2);
g.AddEdge(2, 5, 4);
g.AddEdge(3, 4, 9);
g.AddEdge(3, 5, 14);
g.AddEdge(4, 5, 10);
g.AddEdge(5, 6, 2);
g.AddEdge(6, 7, 1);
g.AddEdge(6, 8, 6);
g.AddEdge(7, 8, 7);
g.shortestPath(0, 14);
}
}
|
Javascript
const INF = 0x3f3f3f3f;
class Graph {
constructor(V)
{
this.V = V;
this.adj = Array.from({ length: V }, () => []);
}
addEdge(u, v, w) {
this.adj[u].push([v, w]);
this.adj[v].push([u, w]);
}
shortestPath(src, W)
{
const dist = Array.from({ length: this.V }, () => [INF, null]);
dist[src][0] = 0;
const B = Array.from({ length: W * this.V + 1 }, () => []);
B[0].push(src);
let idx = 0;
while (true)
{
while (B[idx].length === 0 && idx < W * this.V) {
idx += 1;
}
if (idx === W * this.V) {
break;
}
const u = B[idx].shift();
for (const [v, weight] of this.adj[u]) {
const du = dist[u][0];
let dv = dist[v][0];
if (dv > du + weight)
{
if (dv !== INF) {
B[dv].splice(dist[v][1], 1);
}
dist[v][0] = du + weight;
dv = dist[v][0];
B[dv].push(v);
dist[v][1] = B[dv].length - 1;
}
}
}
console.log("Vertex Distance from Source");
for (let i = 0; i < this.V; i++) {
console.log(`${i} ${dist[i][0]}`);
}
}
}
const V = 9;
const W = 14;
const g = new Graph(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.shortestPath(0, W);
|
Java
import java.util.*;
public class Graph {
static final int INF = Integer.MAX_VALUE;
private int V;
private ArrayList<ArrayList<Tuple> > adj;
public Graph(int v)
{
this.V = v;
this.adj = new ArrayList<ArrayList<Tuple> >();
for (int i = 0; i < v; i++)
this.adj.add(new ArrayList<Tuple>());
}
public void AddEdge(int u, int v, int w)
{
adj.get(u).add(new Tuple(v, w));
adj.get(v).add(new Tuple(u, w));
}
public void shortestPath(int src, int W)
{
int[] dist = new int[V];
Arrays.fill(dist, INF);
ArrayList<Integer>[] B = new ArrayList[W * V + 1];
for (int i = 0; i < W * V + 1; i++)
B[i] = new ArrayList<Integer>();
B[0].add(src);
dist[src] = 0;
int idx = 0;
while (true) {
while (B[idx].size() == 0 && idx < W * V)
idx++;
if (idx == W * V)
break;
int u = B[idx].get(0);
B[idx].remove(0);
for (Tuple i : adj.get(u)) {
int v = i.v;
int weight = i.w;
int du = dist[u];
int dv = dist[v];
if (dv > du + weight) {
dist[v] = du + weight;
dv = dist[v];
B[dv].add(0, v);
}
}
}
System.out.println("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
System.out.println(i + "\t\t" + dist[i]);
}
static class Tuple {
int v, w;
Tuple(int v, int w)
{
this.v = v;
this.w = w;
}
}
public static void main(String[] args)
{
int V = 9;
Graph g = new Graph(V);
g.AddEdge(0, 1, 4);
g.AddEdge(0, 7, 8);
g.AddEdge(1, 2, 8);
g.AddEdge(1, 7, 11);
g.AddEdge(2, 3, 7);
g.AddEdge(2, 8, 2);
g.AddEdge(2, 5, 4);
g.AddEdge(3, 4, 9);
g.AddEdge(3, 5, 14);
g.AddEdge(4, 5, 10);
g.AddEdge(5, 6, 2);
g.AddEdge(6, 7, 1);
g.AddEdge(6, 8, 6);
g.AddEdge(7, 8, 7);
g.shortestPath(0, 14);
}
}
|
Output
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
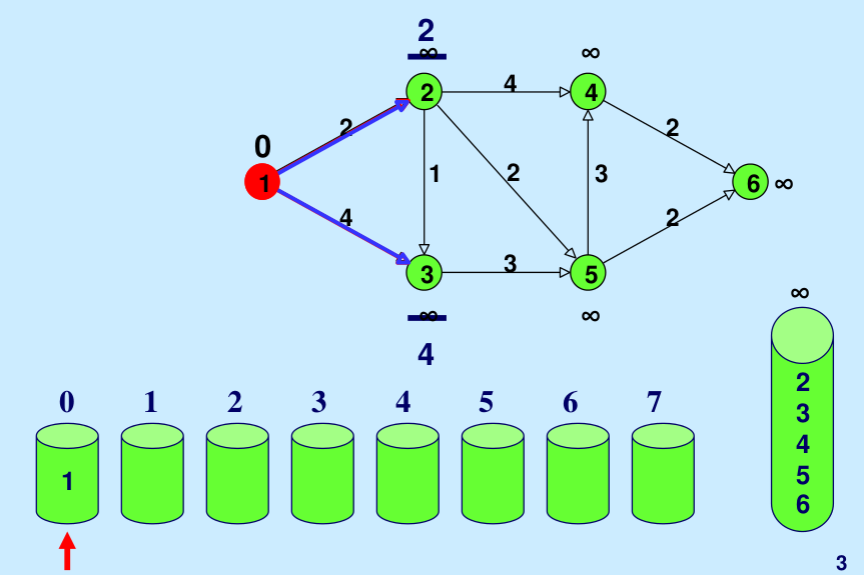
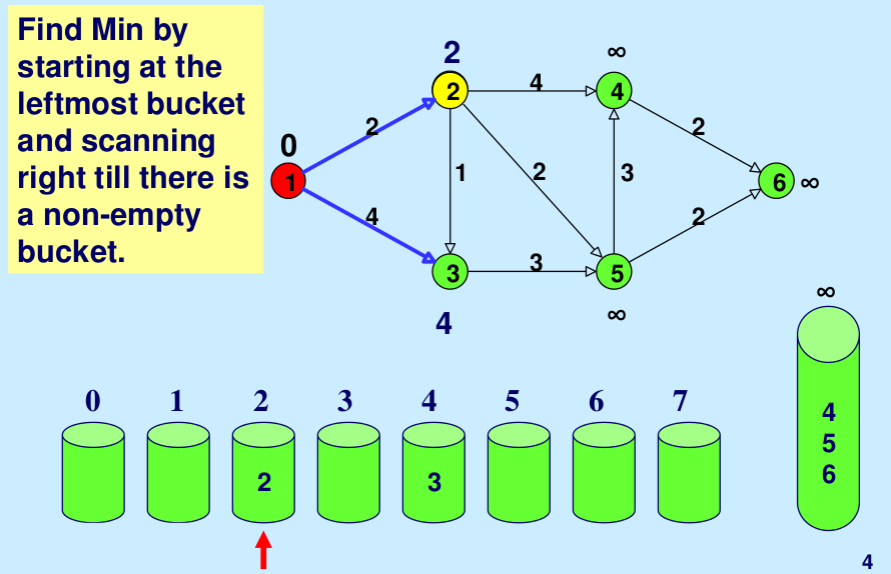
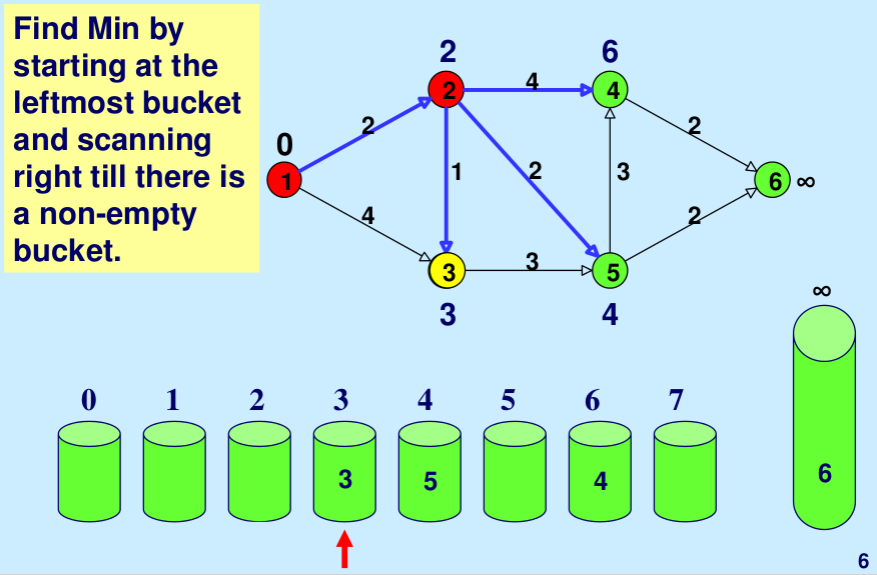
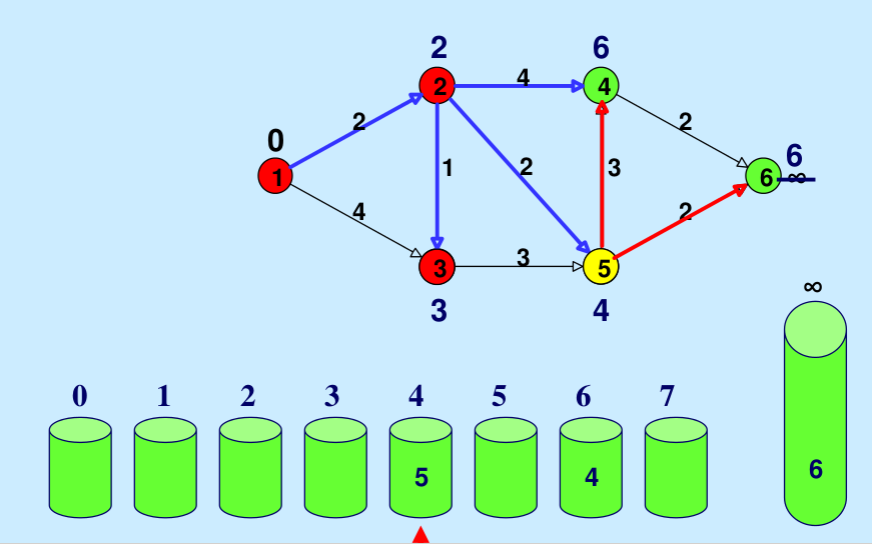
Illustration: Below is the step-by-step illustration taken from here. 






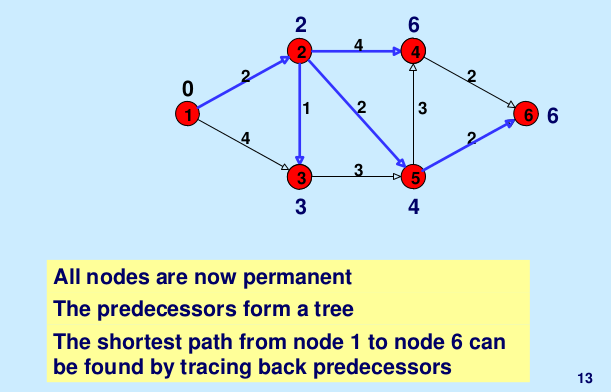
Time Complexity: The time complexity of the above implementation is O(V*W). Here V is the number of vertices in the graph and W is the maximum weight of the edge.
Space Complexity: The space complexity of the above implementation is O(V*W). In the above implementation, we have used a 2D vector to store the distances of each vertex from the source vertex.
Dial’s algorithm is an optimized version of Dijkstra’s algorithm for finding the shortest paths in a graph with non-negative edge weights. It is particularly useful when the range of the edge weights is small, meaning that the weights only take on a small number of distinct values.
Here are the steps of Dial’s algorithm:
- Initialize a set of buckets, where each bucket i contains all nodes with a current shortest path estimate of i.
Start with the source node s and set its shortest path estimate to 0.
- For each node v adjacent to s, add it to the bucket corresponding to its distance from s.
While there are non-empty buckets:
a. Find the non-empty bucket with the smallest index i.
b. Remove the node u with the smallest shortest path estimate from the bucket.
c. For each node v adjacent to u:
- If the shortest path estimate for v is greater than the new estimate via u, update v’s estimate and move it to the corresponding bucket.
Return the shortest path estimates for all nodes.
- The idea behind Dial’s algorithm is to avoid scanning all nodes in each iteration of Dijkstra’s algorithm. Instead, we group the nodes into buckets based on their shortest path estimate, and only process the nodes with the smallest estimate in each iteration. This reduces the number of nodes that need to be processed and speeds up the algorithm, especially when the range of the edge weights is small.
Advantages:
- Dial’s algorithm can be much faster than Dijkstra’s algorithm for graphs with small range weights.
- It has a time complexity of O(n + m), where n is the number of nodes and m is the number of edges.
- It is easy to implement and modify from Dijkstra’s algorithm.
Disadvantages:
- Dial’s algorithm is only applicable when the range of the edge weights is small. For graphs with large range weights, Dijkstra’s algorithm may be faster.
- The space complexity of Dial’s algorithm is O(nW), where W is the range of the edge weights. This can be a significant drawback for large values of W.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...