Dial’s Algorithm (Optimized Dijkstra for small range weights)
Dijkstra’s shortest path algorithm runs in O(Elog V) time when implemented with adjacency list representation (See C implementation and STL based C++ implementations for details).
Input : Source = 0, Maximum Weight W = 14
Output :
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14Can we optimize Dijkstra’s shortest path algorithm to work better than O(E log V) if maximum weight is small (or range of edge weights is small)?
For example, in the above diagram, maximum weight is 14. Many a times the range of weights on edges in is in small range (i.e. all edge weight can be mapped to 0, 1, 2.. w where w is a small number). In that case, Dijkstra’s algorithm can be modified by using different data structure, buckets, which is called dial implementation of dijkstra’s algorithm. time complexity is O(E + WV) where W is maximum weight on any edge of graph, so we can see that, if W is small then this implementation runs much faster than traditional algorithm. Following are important observations.
Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.
In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.
- Maximum distance between any two node can be at max w(V – 1) (w is maximum edge weight and we can have at max V-1 edges between two vertices).
- In Dijkstra algorithm, distances are finalized in non-decreasing, i.e., distance of the closer (to given source) vertices is finalized before the distant vertices.
Below is complete algorithm:
- Maintains some buckets, numbered 0, 1, 2,…,wV.
- Bucket k contains all temporarily labeled nodes with distance equal to k.
- Nodes in each bucket are represented by list of vertices.
- Buckets 0, 1, 2,..wV are checked sequentially until the first non-empty bucket is found. Each node contained in the first non-empty bucket has the minimum distance label by definition.
- One by one, these nodes with minimum distance label are permanently labeled and deleted from the bucket during the scanning process.
- Thus operations involving vertex include:
- Checking if a bucket is empty
- Adding a vertex to a bucket
- Deleting a vertex from a bucket.
- The position of a temporarily labeled vertex in the buckets is updated accordingly when the distance label of a vertex changes.
- Process repeated until all vertices are permanently labeled (or distances of all vertices are finalized).
Since the maximum distance can be w(V – 1), we create wV buckets (more for simplicity of code) for implementation of algorithm which can be large if w is big.
// C++ Program for Dijkstra's dial implementation#include<bits/stdc++.h>using namespace std;# define INF 0x3f3f3f3f // This class represents a directed graph using// adjacency list representationclass Graph{ int V; // No. of vertices // In a weighted graph, we need to store vertex // and weight pair for every edge list< pair<int, int> > *adj; public: Graph(int V); // Constructor // function to add an edge to graph void addEdge(int u, int v, int w); // prints shortest path from s void shortestPath(int s, int W);}; // Allocates memory for adjacency listGraph::Graph(int V){ this->V = V; adj = new list< pair<int, int> >[V];} // adds edge between u and v of weight wvoid Graph::addEdge(int u, int v, int w){ adj[u].push_back(make_pair(v, w)); adj[v].push_back(make_pair(u, w));} // Prints shortest paths from src to all other vertices.// W is the maximum weight of an edgevoid Graph::shortestPath(int src, int W){ /* With each distance, iterator to that vertex in its bucket is stored so that vertex can be deleted in O(1) at time of updation. So dist[i].first = distance of ith vertex from src vertex dits[i].second = iterator to vertex i in bucket number */ vector<pair<int, list<int>::iterator> > dist(V); // Initialize all distances as infinite (INF) for (int i = 0; i < V; i++) dist[i].first = INF; // Create buckets B[]. // B[i] keep vertex of distance label i list<int> B[W * V + 1]; B[0].push_back(src); dist[src].first = 0; // int idx = 0; while (1) { // Go sequentially through buckets till one non-empty // bucket is found while (B[idx].size() == 0 && idx < W*V) idx++; // If all buckets are empty, we are done. if (idx == W * V) break; // Take top vertex from bucket and pop it int u = B[idx].front(); B[idx].pop_front(); // Process all adjacents of extracted vertex 'u' and // update their distanced if required. for (auto i = adj[u].begin(); i != adj[u].end(); ++i) { int v = (*i).first; int weight = (*i).second; int du = dist[u].first; int dv = dist[v].first; // If there is shorted path to v through u. if (dv > du + weight) { // If dv is not INF then it must be in B[dv] // bucket, so erase its entry using iterator // in O(1) if (dv != INF) B[dv].erase(dist[v].second); // updating the distance dist[v].first = du + weight; dv = dist[v].first; // pushing vertex v into updated distance's bucket B[dv].push_front(v); // storing updated iterator in dist[v].second dist[v].second = B[dv].begin(); } } } // Print shortest distances stored in dist[] printf("Vertex Distance from Source\n"); for (int i = 0; i < V; ++i) printf("%d %d\n", i, dist[i].first);} // Driver program to test methods of graph classint main(){ // create the graph given in above fugure int V = 9; Graph g(V); // making above shown graph g.addEdge(0, 1, 4); g.addEdge(0, 7, 8); g.addEdge(1, 2, 8); g.addEdge(1, 7, 11); g.addEdge(2, 3, 7); g.addEdge(2, 8, 2); g.addEdge(2, 5, 4); g.addEdge(3, 4, 9); g.addEdge(3, 5, 14); g.addEdge(4, 5, 10); g.addEdge(5, 6, 2); g.addEdge(6, 7, 1); g.addEdge(6, 8, 6); g.addEdge(7, 8, 7); // maximum weighted edge - 14 g.shortestPath(0, 14); return 0;} |
Output:
Vertex Distance from Source 0 0 1 4 2 12 3 19 4 21 5 11 6 9 7 8 8 14
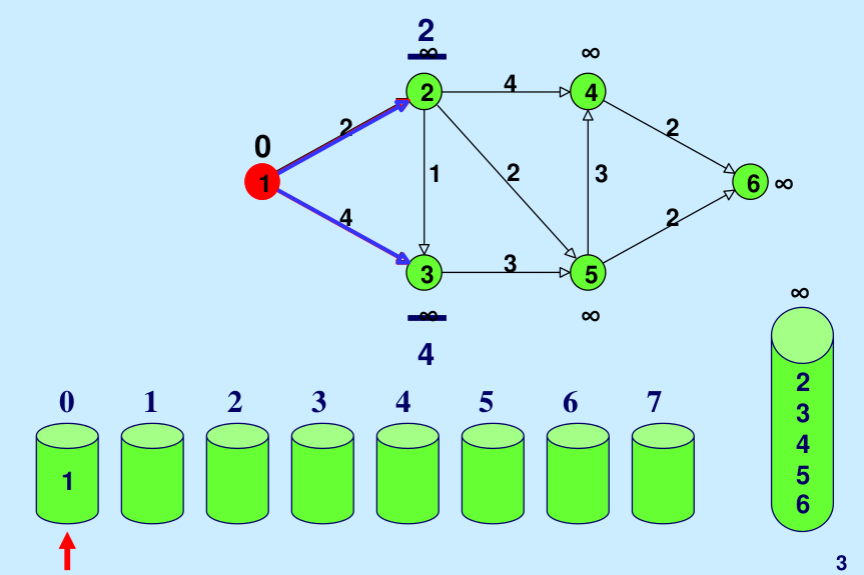
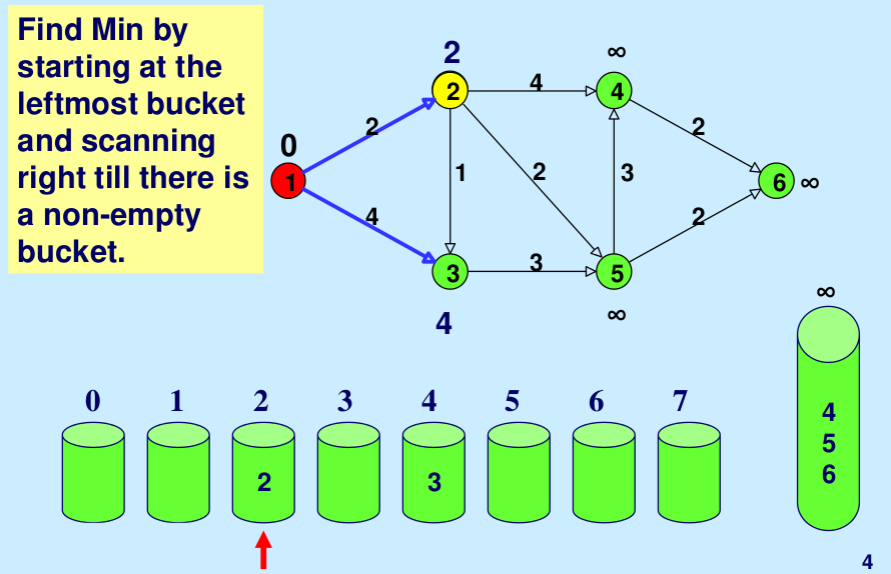
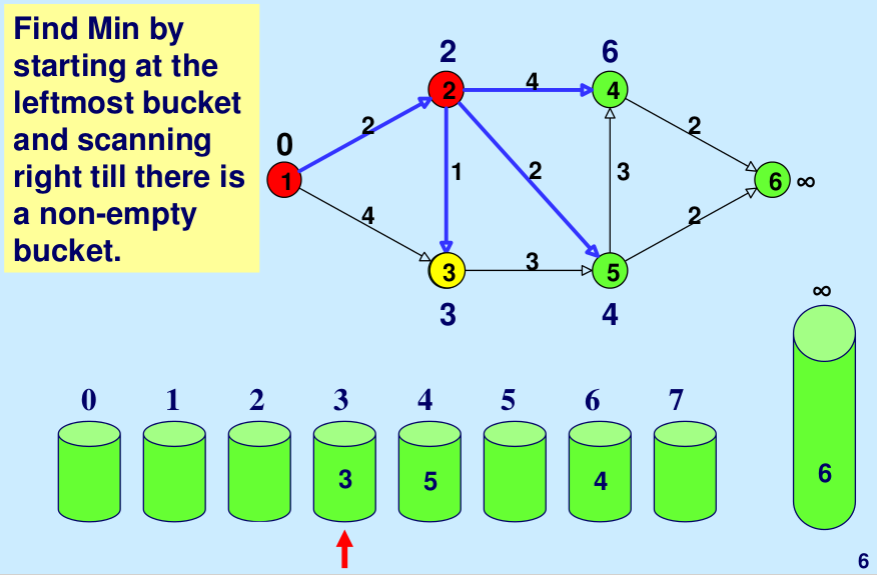
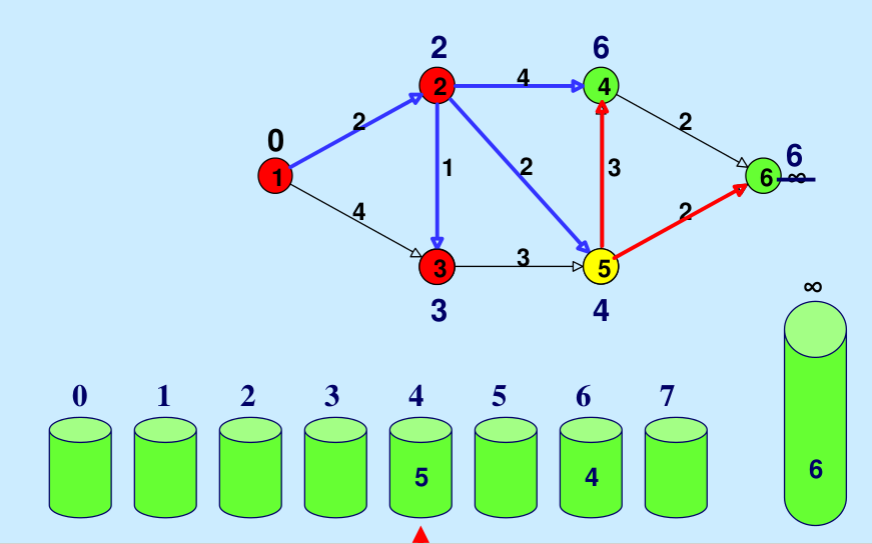
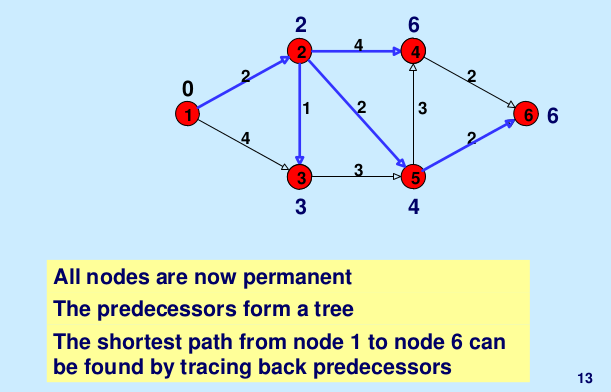
Below is step by step illustration taken from here.
This article is contributed by Utkarsh Trivedi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
