DFA based division
Last Updated :
09 Aug, 2022
Deterministic Finite Automaton (DFA) can be used to check whether a number “num” is divisible by “k” or not. If the number is not divisible, remainder can also be obtained using DFA.
We consider the binary representation of ‘num’ and build a DFA with k states. The DFA has transition function for both 0 and 1. Once the DFA is built, we process ‘num’ over the DFA to get remainder.
Let us walk through an example. Suppose we want to check whether a given number ‘num’ is divisible by 3 or not. Any number can be written in the form: num = 3*a + b where ‘a’ is the quotient and ‘b’ is the remainder.
For 3, there can be 3 states in DFA, each corresponding to remainder 0, 1 and 2. And each state can have two transitions corresponding 0 and 1 (considering the binary representation of given ‘num’).
The transition function F(p, x) = q tells that on reading alphabet x, we move from state p to state q. Let us name the states as 0, 1 and 2. The initial state will always be 0. The final state indicates the remainder. If the final state is 0, the number is divisible.
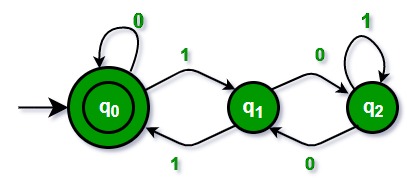
In the above diagram, double circled state is final state.
1. When we are at state 0 and read 0, we remain at state 0.
2. When we are at state 0 and read 1, we move to state 1, why? The number so formed(1) in decimal gives remainder 1.
3. When we are at state 1 and read 0, we move to state 2, why? The number so formed(10) in decimal gives remainder 2.
4. When we are at state 1 and read 1, we move to state 0, why? The number so formed(11) in decimal gives remainder 0.
5. When we are at state 2 and read 0, we move to state 1, why? The number so formed(100) in decimal gives remainder 1.
6. When we are at state 2 and read 1, we remain at state 2, why? The number so formed(101) in decimal gives remainder 2.
The transition table looks like following:
state 0 1
_____________
0 0 1
1 2 0
2 1 2
Let us check whether 6 is divisible by 3?
Binary representation of 6 is 110
state = 0
1. state=0, we read 1, new state=1
2. state=1, we read 1, new state=0
3. state=0, we read 0, new state=0
Since the final state is 0, the number is divisible by 3.
Let us take another example number as 4
state=0
1. state=0, we read 1, new state=1
2. state=1, we read 0, new state=2
3. state=2, we read 0, new state=1
Since, the final state is not 0, the number is not divisible by 3. The remainder is 1.
Note that the final state gives the remainder.
We can extend the above solution for any value of k. For a value k, the states would be 0, 1, …. , k-1. How to calculate the transition if the decimal equivalent of the binary bits seen so far, crosses the range k? If we are at state p, we have read p (in decimal). Now we read 0, new read number becomes 2*p. If we read 1, new read number becomes 2*p+1. The new state can be obtained by subtracting k from these values (2p or 2p+1) where 0 <= p < k.
Based on the above approach, following is the working code:
C++
#include <bits/stdc++.h>
using namespace std;
void preprocess(int k, int Table[][2])
{
int trans0, trans1;
for (int state = 0; state < k; ++state)
{
trans0 = state << 1;
Table[state][0] = (trans0 < k) ?
trans0 : trans0 - k;
trans1 = (state << 1) + 1;
Table[state][1] = (trans1 < k) ?
trans1 : trans1 - k;
}
}
void isDivisibleUtil(int num, int* state,
int Table[][2])
{
if (num != 0)
{
isDivisibleUtil(num >> 1, state, Table);
*state = Table[*state][num & 1];
}
}
int isDivisible (int num, int k)
{
int (*Table)[2] = (int (*)[2])malloc(k*sizeof(*Table));
preprocess(k, Table);
int state = 0;
isDivisibleUtil(num, &state, Table);
return state;
}
int main()
{
int num = 47;
int k = 5;
int remainder = isDivisible (num, k);
if (remainder == 0)
cout << "Divisible\n";
else
cout << "Not Divisible: Remainder is "
<< remainder;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
void preprocess(int k, int Table[][2])
{
int trans0, trans1;
for (int state=0; state<k; ++state)
{
trans0 = state<<1;
Table[state][0] = (trans0 < k)? trans0: trans0-k;
trans1 = (state<<1) + 1;
Table[state][1] = (trans1 < k)? trans1: trans1-k;
}
}
void isDivisibleUtil(int num, int* state, int Table[][2])
{
if (num != 0)
{
isDivisibleUtil(num>>1, state, Table);
*state = Table[*state][num&1];
}
}
int isDivisible (int num, int k)
{
int (*Table)[2] = (int (*)[2])malloc(k*sizeof(*Table));
preprocess(k, Table);
int state = 0;
isDivisibleUtil(num, &state, Table);
return state;
}
int main()
{
int num = 47;
int k = 5;
int remainder = isDivisible (num, k);
if (remainder == 0)
printf("Divisible\n");
else
printf("Not Divisible: Remainder is %d\n", remainder);
return 0;
}
|
Java
import java.util.*;
class GFG {
static void preprocess(int k, int[][] Table)
{
int trans0, trans1;
for (int state = 0; state < k; ++state)
{
trans0 = state << 1;
Table[state][0]
= (trans0 < k) ? trans0 : trans0 - k;
trans1 = (state << 1) + 1;
Table[state][1]
= (trans1 < k) ? trans1 : trans1 - k;
}
}
static int isDivisibleUtil(int num, int state,
int[][] Table)
{
if (num != 0) {
state = isDivisibleUtil(num >> 1, state, Table);
state = Table[state][num & 1];
}
return state;
}
static int isDivisible(int num, int k)
{
int[][] Table = new int[k][2];
for (int i = 0; i < k; i++) {
Table[i][0] = 0;
Table[i][1] = 0;
}
preprocess(k, Table);
int state = 0;
state = isDivisibleUtil(num, state, Table);
return state;
}
public static void main(String[] args)
{
int num = 47;
int k = 5;
int remainder = isDivisible(num, k);
if (remainder == 0)
System.out.println("Divisible");
else
System.out.println(
"Not Divisible: Remainder is " + remainder);
}
}
|
Python3
def preprocess(k, Table):
for state in range(k):
trans0 = state << 1
if (trans0 < k):
Table[state][0] = trans0
else:
Table[state][0] = trans0 - k
trans1 = (state << 1) + 1
if trans1 < k:
Table[state][1] = trans1
else:
Table[state][1] = trans1 - k
def isDivisibleUtil(num, state, Table):
if (num != 0):
state = isDivisibleUtil(num >> 1, state, Table)
state = Table[state][num & 1]
return state
def isDivisible(num, k):
Table = [None for i in range(k)]
for i in range(k):
Table[i] = [0, 0]
preprocess(k, Table)
state = 0
state = isDivisibleUtil(num, state, Table)
return state
num = 47
k = 5
remainder = isDivisible(num, k)
if (remainder == 0):
print("Divisible")
else:
print("Not Divisible: Remainder is", remainder)
|
C#
using System;
class GFG
{
static void preprocess(int k, int[, ] Table)
{
int trans0, trans1;
for (int state = 0; state < k; ++state) {
trans0 = state << 1;
Table[state, 0]
= (trans0 < k) ? trans0 : trans0 - k;
trans1 = (state << 1) + 1;
Table[state, 1]
= (trans1 < k) ? trans1 : trans1 - k;
}
}
static int isDivisibleUtil(int num, int state,
int[, ] Table)
{
if (num != 0) {
state = isDivisibleUtil(num >> 1, state, Table);
state = Table[state, num & 1];
}
return state;
}
static int isDivisible(int num, int k)
{
int[, ] Table = new int[k, 2];
for (int i = 0; i < k; i++) {
Table[i, 0] = 0;
Table[i, 1] = 0;
}
preprocess(k, Table);
int state = 0;
state = isDivisibleUtil(num, state, Table);
return state;
}
public static void Main(string[] args)
{
int num = 47;
int k = 5;
int remainder = isDivisible(num, k);
if (remainder == 0)
Console.WriteLine("Divisible");
else
Console.WriteLine("Not Divisible: Remainder is "
+ remainder);
}
}
|
Javascript
function preprocess(k, Table)
{
let trans0, trans1;
for (let state = 0; state < k; ++state)
{
trans0 = state << 1;
Table[state][0] = (trans0 < k) ?
trans0 : trans0 - k;
trans1 = (state << 1) + 1;
Table[state][1] = (trans1 < k) ?
trans1 : trans1 - k;
}
}
function isDivisibleUtil(num, state, Table)
{
if (num != 0)
{
state = isDivisibleUtil(num >> 1, state, Table);
state = Table[state][num & 1];
}
return state;
}
function isDivisible (num, k)
{
Table = new Array(k);
for (let i = 0; i < k; i++)
Table[i] = [0, 0];
preprocess(k, Table);
let state = 0;
state = isDivisibleUtil(num, state, Table);
return state;
}
let num = 47;
let k = 5;
let remainder = isDivisible (num, k);
if (remainder == 0)
console.log("Divisible");
else
console.log("Not Divisible: Remainder is " + remainder);
|
Output:
Not Divisible: Remainder is 2
Time Complexity: O(k)
DFA based division can be useful if we have a binary stream as input and we want to check for divisibility of the decimal value of stream at any time.
Related Articles:
Check divisibility in a binary stream
Check if a stream is Multiple of 3
This article is compiled by Aashish Barnwal and reviewed by GeeksforGeeks team.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...