Detecting negative cycle using Floyd Warshall

We are given a directed graph. We need compute whether the graph has negative cycle or not. A negative cycle is one in which the overall sum of the cycle comes negative.

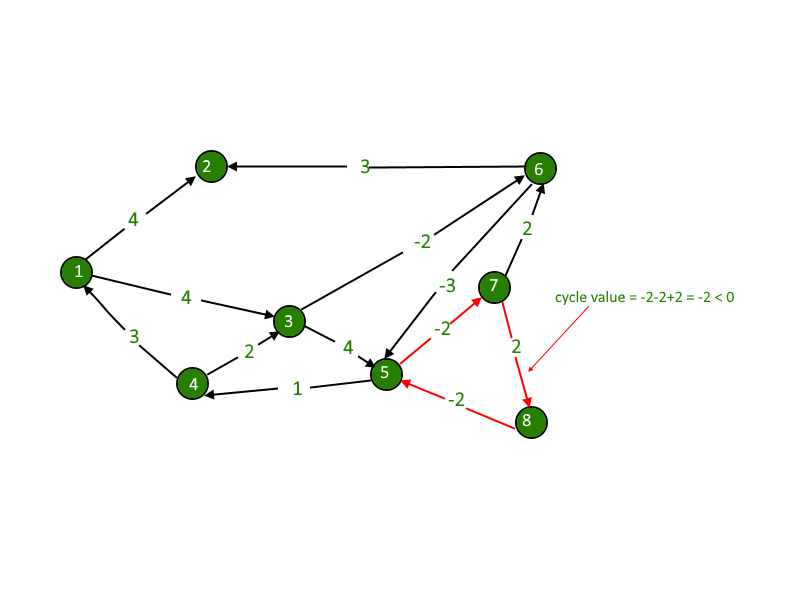
Negative weights are found in various applications of graphs. For example, instead of paying cost for a path, we may get some advantage if we follow the path.

Examples: 

Input : 4 4
        0 1 1
        1 2 -1
        2 3 -1
        3 0 -1

Output : Yes
The graph contains a negative cycle.

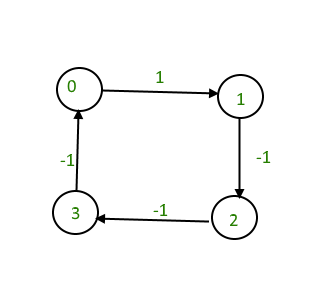
We have discussed Bellman Ford Algorithm based solution for this problem.
In this post, Floyd Warshall Algorithm based solution is discussed that works for both connected and disconnected graphs.
Distance of any node from itself is always zero. But in some cases, as in this example, when we traverse further from 4 to 1, the distance comes out to be -2, i.e. distance of 1 from 1 will become -2. This is our catch, we just have to check the nodes distance from itself and if it comes out to be negative, we will detect the required negative cycle.

Implementation:

C++

// C++ Program to check if there is a negative weight
// cycle using Floyd Warshall Algorithm
#include<bits/stdc++.h>
using namespace std;

// Number of vertices in the graph
#define V 4

/* Define Infinite as a large enough value. This
   value will be used for vertices not connected
   to each other */
#define INF 99999

// A function to print the solution matrix
void printSolution(int dist[][V]);

// Returns true if graph has negative weight cycle
// else false.
bool negCyclefloydWarshall(int graph[][V])
{
    /* dist[][] will be the output matrix that will
       finally have the shortest
    distances between every pair of vertices */
    int dist[V][V], i, j, k;

    /* Initialize the solution matrix same as input
      graph matrix. Or we can say the initial values
      of shortest distances are based on shortest
      paths considering no intermediate vertex. */
    for (i = 0; i < V; i++)
        for (j = 0; j < V; j++)
            dist[i][j] = graph[i][j];

    /* Add all vertices one by one to the set of
       intermediate vertices.
    ---> Before start of a iteration, we have shortest
         distances between all pairs of vertices such
         that the shortest distances consider only the
         vertices in set {0, 1, 2, .. k-1} as intermediate
         vertices.
    ----> After the end of a iteration, vertex no. k is
          added to the set of intermediate vertices and
          the set becomes {0, 1, 2, .. k} */
    for (k = 0; k < V; k++)
    {
        // Pick all vertices as source one by one
        for (i = 0; i < V; i++)
        {
            // Pick all vertices as destination for the
            // above picked source
            for (j = 0; j < V; j++)
            {
                // If vertex k is on the shortest path from
                // i to j, then update the value of dist[i][j]
                if (dist[i][k] + dist[k][j] < dist[i][j])
                        dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }

    // If distance of any vertex from itself
    // becomes negative, then there is a negative
    // weight cycle.
    for (int i = 0; i < V; i++)
        if (dist[i][i] < 0)
            return true;
    return false;
}

 // driver program
int main()
{
    /* Let us create the following weighted graph
            1
    (0)----------->(1)
    /|\             |
     |              |
  -1 |              | -1
     |             \|/
    (3)<-----------(2)
        -1       */

    int graph[V][V] = { {0   , 1   , INF , INF},
                        {INF , 0   , -1  , INF},
                        {INF , INF , 0   ,  -1},
                        {-1  , INF , INF ,   0}};

    if (negCyclefloydWarshall(graph))
       cout << "Yes";
    else
       cout << "No";
    return 0;
}

Java

// Java Program to check if there is a negative weight
// cycle using Floyd Warshall Algorithm
class GFG
{

    // Number of vertices in the graph
    static final int V = 4;

    /* Define Infinite as a large enough value. This
    value will be used for vertices not connected
    to each other */
    static final int INF = 99999;

    // Returns true if graph has negative weight cycle
    // else false.
    static boolean negCyclefloydWarshall(int graph[][])
    {

        /* dist[][] will be the output matrix that will
        finally have the shortest
        distances between every pair of vertices */
        int dist[][] = new int[V][V], i, j, k;

        /* Initialize the solution matrix same as input
        graph matrix. Or we can say the initial values
        of shortest distances are based on shortest
        paths considering no intermediate vertex. */
        for (i = 0; i < V; i++)
            for (j = 0; j < V; j++)
                dist[i][j] = graph[i][j];

        /* Add all vertices one by one to the set of
        intermediate vertices.
        ---> Before start of a iteration, we have shortest
            distances between all pairs of vertices such
            that the shortest distances consider only the
            vertices in set {0, 1, 2, .. k-1} as intermediate
            vertices.
        ----> After the end of a iteration, vertex no. k is
            added to the set of intermediate vertices and
            the set becomes {0, 1, 2, .. k} */
        for (k = 0; k < V; k++)
        {

            // Pick all vertices as source one by one
            for (i = 0; i < V; i++)
            {

                // Pick all vertices as destination for the
                // above picked source
                for (j = 0; j < V; j++)
                {

                    // If vertex k is on the shortest path from
                    // i to j, then update the value of dist[i][j]
                    if (dist[i][k] + dist[k][j] < dist[i][j])
                            dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }

        // If distance of any vertex from itself
        // becomes negative, then there is a negative
        // weight cycle.
        for (i = 0; i < V; i++)
            if (dist[i][i] < 0)
                return true;

        return false;
    }

    // Driver code
    public static void main (String[] args)
    {

    /* Let us create the following weighted graph
                1
        (0)----------->(1)
        /|\               |
         |               |
      -1 |               | -1
         |                \|/
        (3)<-----------(2)
            -1     */

        int graph[][] = { {0, 1, INF, INF},
                          {INF, 0, -1, INF},
                          {INF, INF, 0, -1},
                          {-1, INF, INF, 0}};

        if (negCyclefloydWarshall(graph))
            System.out.print("Yes");
        else
            System.out.print("No");
    }
}

// This code is contributed by Anant Agarwal.

Python3

# Python Program to check
# if there is a
# negative weight
# cycle using Floyd
# Warshall Algorithm


# Number of vertices
# in the graph
V = 4

# Define Infinite as a
# large enough value. This
# value will be used
#for vertices not connected
# to each other
INF = 99999

# Returns true if graph has
# negative weight cycle
# else false.
def negCyclefloydWarshall(graph):

    # dist[][] will be the
    # output matrix that will
    # finally have the shortest
    # distances between every
    # pair of vertices
    dist=[[0 for i in range(V+1)]for j in range(V+1)]

    # Initialize the solution
    # matrix same as input
    # graph matrix. Or we can
    # say the initial values
    # of shortest distances
    # are based on shortest
    # paths considering no
    # intermediate vertex.
    for i in range(V):
        for j in range(V):
            dist[i][j] = graph[i][j]

    ''' Add all vertices one
        by one to the set of
        intermediate vertices.
    ---> Before start of a iteration,
         we have shortest
        distances between all pairs
        of vertices such
        that the shortest distances
        consider only the
        vertices in set {0, 1, 2, .. k-1}
        as intermediate vertices.
    ----> After the end of a iteration,
          vertex no. k is
        added to the set of
        intermediate vertices and
        the set becomes {0, 1, 2, .. k} '''
    for k in range(V):

        # Pick all vertices
        # as source one by one
        for i in range(V):

            # Pick all vertices as
            # destination for the
            # above picked source
            for j in range(V):

                # If vertex k is on
                # the shortest path from
                # i to j, then update
                # the value of dist[i][j]
                if (dist[i][k] + dist[k][j] < dist[i][j]):
                        dist[i][j] = dist[i][k] + dist[k][j]

    # If distance of any
    # vertex from itself
    # becomes negative, then
    # there is a negative
    # weight cycle.
    for i in range(V):
        if (dist[i][i] < 0):
            return True

    return False


# Driver code


''' Let us create the
    following weighted graph
            1
    (0)----------->(1)
    /|\               |
     |               |
  -1 |               | -1
     |                \|/
    (3)<-----------(2)
        -1     '''

graph = [ [0, 1, INF, INF],
          [INF, 0, -1, INF],
          [INF, INF, 0, -1],
          [-1, INF, INF, 0]]

if (negCyclefloydWarshall(graph)):
    print("Yes")
else:
    print("No")

# This code is contributed
# by Anant Agarwal.

C#

// C# Program to check if there
// is a negative weight cycle
// using Floyd Warshall Algorithm

using System;

namespace Cycle
{
public class GFG
{


    // Number of vertices in the graph
    static int V = 4;

    /* Define Infinite as a large enough value. This
    value will be used for vertices not connected
    to each other */
    static int INF = 99999;

    // Returns true if graph has negative weight cycle
    // else false.
    static bool negCyclefloydWarshall(int [,]graph)
    {

        /* dist[][] will be the output matrix that will
        finally have the shortest
        distances between every pair of vertices */
        int [,]dist = new int[V,V];
        int i, j, k;

        /* Initialize the solution matrix same as input
        graph matrix. Or we can say the initial values
        of shortest distances are based on shortest
        paths considering no intermediate vertex. */
        for (i = 0; i < V; i++)
            for (j = 0; j < V; j++)
                dist[i,j] = graph[i,j];

        /* Add all vertices one by one to the set of
        intermediate vertices.
        ---> Before start of a iteration, we have shortest
            distances between all pairs of vertices such
            that the shortest distances consider only the
            vertices in set {0, 1, 2, .. k-1} as intermediate
            vertices.
        ----> After the end of a iteration, vertex no. k is
            added to the set of intermediate vertices and
            the set becomes {0, 1, 2, .. k} */
        for (k = 0; k < V; k++)
        {

            // Pick all vertices as source one by one
            for (i = 0; i < V; i++)
            {

                // Pick all vertices as destination for the
                // above picked source
                for (j = 0; j < V; j++)
                {

                    // If vertex k is on the shortest path from
                    // i to j, then update the value of dist[i][j]
                    if (dist[i,k] + dist[k,j] < dist[i,j])
                            dist[i,j] = dist[i,k] + dist[k,j];
                }
            }
        }

        // If distance of any vertex from itself
        // becomes negative, then there is a negative
        // weight cycle.
        for (i = 0; i < V; i++)
            if (dist[i,i] < 0)
                return true;

        return false;
    }

    // Driver code
    public static void Main()
    {

    /* Let us create the following weighted graph
                1
        (0)----------->(1)
        /|\             |
        |             |
    -1 |             | -1
        |             \|/
        (3)<-----------(2)
            -1     */

        int [,]graph = { {0, 1, INF, INF},
                        {INF, 0, -1, INF},
                        {INF, INF, 0, -1},
                        {-1, INF, INF, 0}};

        if (negCyclefloydWarshall(graph))
            Console.Write("Yes");
        else
            Console.Write("No");
    }
}
}

// This code is contributed by Sam007.

Javascript

<script>

// JavaScript Program to check if there
// is a negative weight cycle
// using Floyd Warshall Algorithm
// Number of vertices in the graph
var V = 4;

/* Define Infinite as a large enough value. This
value will be used for vertices not connected
to each other */
var INF = 99999;

// Returns true if graph has negative weight cycle
// else false.
function negCyclefloydWarshall(graph)
{

    /* dist[][] will be the output matrix that will
    finally have the shortest
    distances between every pair of vertices */
    var dist = Array.from(Array(V), ()=>Array(V));
    var i, j, k;

    /* Initialize the solution matrix same as input
    graph matrix. Or we can say the initial values
    of shortest distances are based on shortest
    paths considering no intermediate vertex. */
    for (i = 0; i < V; i++)
        for (j = 0; j < V; j++)
            dist[i][j] = graph[i][j];

    /* Add all vertices one by one to the set of
    intermediate vertices.
    ---> Before start of a iteration, we have shortest
        distances between all pairs of vertices such
        that the shortest distances consider only the
        vertices in set {0, 1, 2, .. k-1} as intermediate
        vertices.
    ----> After the end of a iteration, vertex no. k is
        added to the set of intermediate vertices and
        the set becomes {0, 1, 2, .. k} */
    for (k = 0; k < V; k++)
    {

        // Pick all vertices as source one by one
        for (i = 0; i < V; i++)
        {

            // Pick all vertices as destination for the
            // above picked source
            for (j = 0; j < V; j++)
            {

                // If vertex k is on the shortest path from
                // i to j, then update the value of dist[i][j]
                if (dist[i][k] + dist[k][j] < dist[i][j])
                        dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }

    // If distance of any vertex from itself
    // becomes negative, then there is a negative
    // weight cycle.
    for (i = 0; i < V; i++)
        if (dist[i][i] < 0)
            return true;
    return false;
}

// Driver code

/* Let us create the following weighted graph
            1
    (0)----------->(1)
    /|\             |
    |             |
-1 |             | -1
    |             \|/
    (3)<-----------(2)
    -1     */

var graph = [ [0, 1, INF, INF],
                [INF, 0, -1, INF],
                [INF, INF, 0, -1],
                [-1, INF, INF, 0]];

if (negCyclefloydWarshall(graph))
    document.write("Yes");
else
    document.write("No");


</script>

Output

Yes

The time complexity of the Floyd Warshall algorithm is O(V^3) where V is the number of vertices in the graph. This is because the algorithm uses a nested loop structure, where the outermost loop runs V times, the middle loop runs V times and the innermost loop also runs V times. Therefore, the total number of iterations is V * V * V which results in O(V^3) time complexity.

The space complexity of the Floyd Warshall algorithm is O(V^2) where V is the number of vertices in the graph. This is because the algorithm uses a 2D array of size V x V to store the shortest distances between every pair of vertices. Therefore, the total space required is V * V which results in O(V^2) space complexity.