Designing Finite Automata from Regular Expression (Set 1)
Last Updated :
20 Nov, 2019
In this article, we will see some popular regular expressions and how we can convert them to finite automata.
-
Even number of a’s : The regular expression for even number of a’s is (b|ab*ab*)*. We can construct a finite automata as shown in Figure 1.
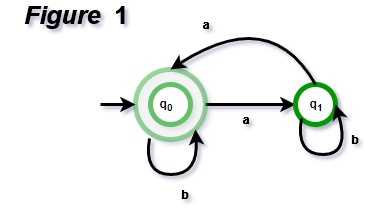
The above automata will accept all strings which have even number of a’s. For zero a’s, it will be in q0 which is final state. For one ‘a’, it will go from q0 to q1 and the string will not be accepted. For two a’s at any positions, it will go from q0 to q1 for 1st ‘a’ and q1 to q0 for second ‘a’. So, it will accept all strings with even number of a’s.
-
String with ‘ab’ as substring : The regular expression for strings with ‘ab’ as substring is (a|b)*ab(a|b)*. We can construct finite automata as shown in Figure 2.

The above automata will accept all string which have ‘ab’ as substring. The automata will remain in initial state q0 for b’s. It will move to q1 after reading ‘a’ and remain in same state for all ‘a’ afterwards. Then it will move to q2 if ‘b’ is read. That means, the string has read ‘ab’ as substring if it reaches q2.
-
String with count of ‘a’ divisible by 3 : The regular expression for strings with count of a divisible by 3 is {a3n | n >= 0}. We can construct automata as shown in Figure 3.

The above automata will accept all string of form a3n. The automata will remain in initial state q0 for ? and it will be accepted. For string ‘aaa’, it will move from q0 to q1 then q1 to q2 and then q2 to q0. For every set of three a’s, it will come to q0, hence accepted. Otherwise, it will be in q1 or q2, hence rejected.
Note : If we want to design a finite automata with number of a’s as 3n+1, same automata can be used with final state as q1 instead of q0.
If we want to design a finite automata with language {akn | n >= 0}, k states are required. We have used k = 3 in our example.
-
Binary numbers divisible by 3 : The regular expression for binary numbers which are divisible by three is (0|1(01*0)*1)*. The examples of binary number divisible by 3 are 0, 011, 110, 1001, 1100, 1111, 10010 etc. The DFA corresponding to binary number divisible by 3 can be shown in Figure 4.

The above automata will accept all binary numbers divisible by 3. For 1001, the automata will go from q0 to q1, then q1 to q2, then q2 to q1 and finally q2 to q0, hence accepted. For 0111, the automata will go from q0 to q0, then q0 to q1, then q1 to q0 and finally q0 to q1, hence rejected.
-
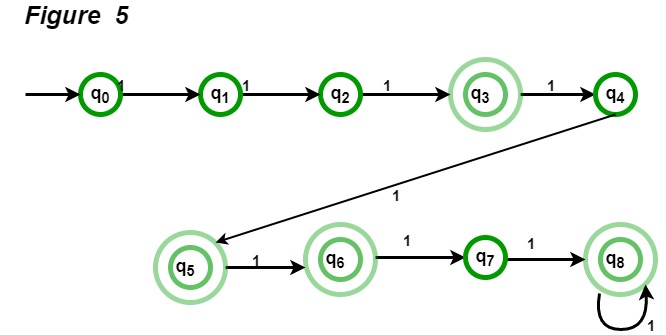
String with regular expression (111 + 11111)* : The string accepted using this regular expression will have 3, 5, 6(111 twice), 8 (11111 once and 111 once), 9 (111 thrice), 10 (11111 twice) and all other counts of 1 afterwards. The DFA corresponding to given regular expression is given in Figure 5.
Question : What will be the minimum number of states for strings with odd number of a’s?
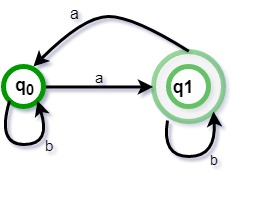
Solution : The regular expression for odd number of a is b*ab*(ab*ab*)* and corresponding automata is given in Figure 6 and minimum number of states are 2.
TOC | Designing Deterministic Finite Automata (Set 1)
This article has been contributed by Sonal Tuteja.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...