Design a Turing Machine for equal number of a’s and b’s

Prerequisite – Turing Machine

Task :
Our task is to design a Turing Machine for an equal number of a’s and b’s.

Analysis :
Here the main thing to analyze that string consist of equal numbers of a’s and b’s can be of 4 types –

Here ‘n’ is the count of a’s or b’s.

a) a^n b^n like aabb

b) b^n a^n like bbaa

c) (ab)^n like abab

d) (ba)^n like baba

Example :

Input-1 :  aabb
Output : Yes

Input-2 : bababa
Output : Yes

Input-3 : aabbbb
Output : No

Input-4 : aaabbaa
Output : No

Approach :

• We have to scan the input from left to right.
• Convert first ‘a’ and first ‘b’ in the scanning to ‘X’, then in the second turn convert second ‘a’ and second ‘b’ to ‘X’ and so on. We have to repeat the process until we convert all a’s and b’s to ‘X’.
• Character scanned in between ‘a’ and ‘b’ will not be changed.

Let us understand this approach by taking a string “aabb” –

1. Scan the input from the left.
2. Our string looks like this –

   

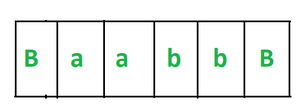
3. Now we see that we get our first ‘a’ at the first position and first b in the third position. We convert these ‘a’ and ‘b’ to ‘X’.

   Now the character ‘a’ we get in between ‘a’ and ‘b’. So it will remain the same. When we read our first b we move our pointer to left. The pointer will move to the left until it gets a Blank(B). Now our string looks like this –

   

4. Our pointer is at Blank(B). We again scan the input from left to right and convert second ‘a’ and second ‘b’ to ‘X’. When we read our second b we move our pointer to left. The pointer will move to the left until it gets a Blank(B). Now our string looks like this –

   

5. We repeat this process until all a’s and b’s converted to X.
6. As we see that we convert all a’s and b’s to ‘X’. Hence our machine will halt.
7. When we analyze this process we see that we convert a’s and b’s to X in pair i.e. in point 3 we convert the first occurrence of a and b to X and then in point 4 we convert the second occurrence of a and b to X. If there are an unequal number of and b then, in this case, some a or b will be left in ou string, otherwise all the character will be converted to X. Hence it will give us a point to proof our condition that our string consists of an equal number of a’s and b’s.

Turing machine :